本文深入解析PCA（主成分分析）的数学原理，通过最小重构误差和最大方差两种视角，详细推导PCA如何实现数据降维，适用于高维数据压缩与特征提取。
PCA（Principal Component Analysis） 和 SVD （参考Singular Value Decomposition）一样，也是数据压缩的一种方法！
1 最小重构误差
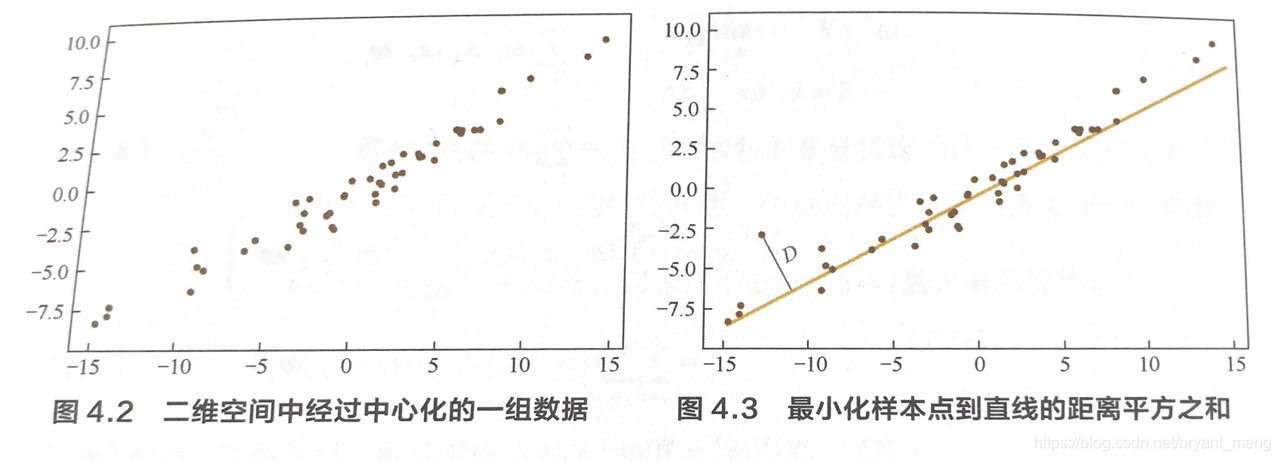
图片来自于葫芦书（《百面机器学习》）
中心化就是每个维度都减去该维度的均值！
原来每一个样本点需要 x x x 和 y y y 两个维度来表示，如果把样本点投影到上图所示的直线上，样本点仅需要一个维度就可以表示了！
这样原来 N N N 个样本点，需要 2 N 2N 2N 的参数量，现在只需要 N + 2 N+2 N+2 的参数量了（达到了降维的目的），2 表示直线的参数量！
问题转化为，最小化原来样本和新样本之间的差值，也即点到直线的距离！！！
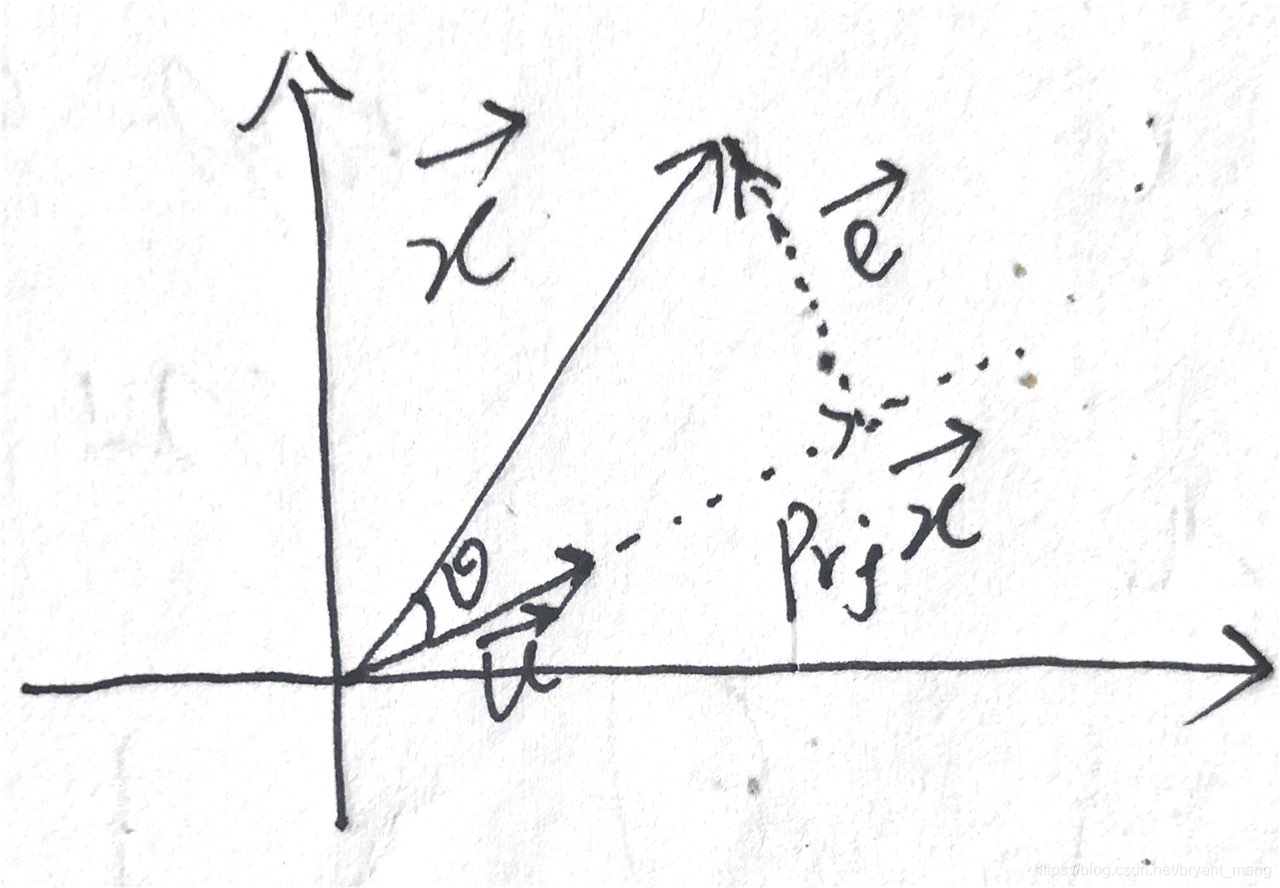
点到支线的距离怎么用向量来表示呢？我们可以画一个上面的图来仔细分析一下！
假设 u ⃗ \vec{u} u 为单位向量，由向量的内积公式（ ⋅ \cdot ⋅ 表示向量的内积运算），我们可知
x ⃗ ⋅ u ⃗ = ∣ x ⃗ ∣ ∣ u ⃗ ∣ c o s θ = ∣ x ⃗ ∣ c o s θ \vec{x}\cdot\vec{u} = |\vec{x}||\vec{u}|cos \theta = |\vec{x}|cos \theta x⋅u=∣x∣∣u∣cosθ=∣x∣cosθ
上面只是投影的距离（向量的模），加上方向就是向量了，所以 x ⃗ \vec{x} x 在 u ⃗ \vec{u} u 上的投影向量为：
P r j u ⃗ x ⃗ = ( ∣ x ⃗ ∣ c o s θ ) u ⃗ = ( x ⃗ ⋅ u ⃗ ) u ⃗ Prj_{\vec{u}}{\vec{x}} = (|\vec{x}|cos \theta)\vec{u} = (\vec{x}\cdot\vec{u})\vec{u} Prjux=(∣x∣cosθ)u=(x⋅u)u
所以
e
⃗
=
x
⃗
−
P
r
j
u
⃗
x
⃗
=
x
⃗
−
(
x
⃗
⋅
u
⃗
)
u
⃗
\vec{e} = \vec{x} - Prj_{\vec{u}}{\vec{x}} = \vec{x}-(\vec{x}\cdot\vec{u})\vec{u}
e=x−Prjux=x−(x⋅u)u
我们简单的表示为如下形式
e ⃗ = x − ( x T u ) u \vec{e} = x - (x^Tu)u e=x−(xTu)u
其中， x x x 和 u u u 表示列向量 x ⃗ \vec{x} x 和 u ⃗ \vec{u} u， x ∈ R n x \in \mathbb{R}^n x∈Rn， u ∈ R n u \in \mathbb{R}^n u∈Rn，因为 u u u 是单位向量，所以 ∣ ∣ u ∣ ∣ = 1 ||u|| = 1 ∣∣u∣∣=1, u T u = 1 u^Tu=1 uTu=1， x T u x^Tu xTu 是标量。
我要最小化误差的平方
J = ∣ ∣ e ⃗ 2 ∣ ∣ = e ⃗ T e ⃗ = [ x − ( x T u ) u ] T [ x − ( x T u ) u ] = [ x T − ( x T u ) u T ] [ x − ( x T u ) u ] （ 因 为 x T 是 标 量 ） = x T x − ( x T u ) x T u − ( x T u ) u T x + ( x T u ) ( x T u ) u T u （ 展 开 ） = x T x − ( x T u ) x T u − ( x T u ) u T x + ( x T u ) 2 （ 因 为 u T u = 1 ） = x T x − ( x T u ) 2 − ( x T u ) 2 + ( x T u ) 2 （ 因 为 x T u = u T x ， 都 是 标 量 ） = x T x − ( x T u ) 2 \begin{aligned} J = ||\vec{e}^2|| = \vec{e}^T\vec{e} &= [x - (x^Tu)u]^T[ x - (x^Tu)u] \\ &= [x^T - (x^Tu)u^T][ x - (x^Tu)u]（因为 x^T 是标量）\\ &=x^Tx - (x^Tu)x^Tu - (x^Tu)u^Tx + (x^Tu)(x^Tu)u^Tu（展开） \\ &=x^Tx - (x^Tu)x^Tu - (x^Tu)u^Tx + (x^Tu)^2（因为 u^Tu=1）\\ &=x^Tx - (x^Tu)^2 - (x^Tu)^2 + (x^Tu)^2（因为 x^Tu = u^Tx，都是标量）\\ &=x^Tx - (x^Tu)^2 \end{aligned} J=∣∣e2∣∣=eTe=[x−(xTu)u]T[x−(xTu)u]=[xT−(xTu)uT][x−(xTu)u]（因为xT是标量）=xTx−(xTu)xTu−(xTu)uTx+(xTu)(xTu)uTu（展开）=xTx−(xTu)xTu−(xTu)uTx+(xTu)2（因为uTu=1）=xTx−(xTu)2−(xTu)2+(xTu)2（因为xTu=uTx，都是标量）=xTx−(xTu)2
如果样本集确定了， x T x x^Tx xTx 也是固定的，唯一会改变的是 ( x T u ) 2 (x^Tu)^2 (xTu)2，所以我们最小化差值的平方 J J J 等价于最大化 ( x T u ) 2 (x^Tu)^2 (xTu)2 的值！
我们再来转化成二次型的形式：
m
a
x
(
x
T
u
)
2
⇔
m
a
x
(
x
T
u
)
(
x
T
u
)
⇔
m
a
x
(
u
T
x
)
(
x
T
u
)
⇔
m
a
x
[
u
T
(
x
x
T
)
u
]
\begin{aligned} max(x^Tu)^2 &\Leftrightarrow max (x^Tu)(x^Tu) \\ &\Leftrightarrow max(u^Tx)(x^Tu) \\ &\Leftrightarrow max [u^T(xx^T)u] \end{aligned}
max(xTu)2⇔max(xTu)(xTu)⇔max(uTx)(xTu)⇔max[uT(xxT)u]
我们一共有
N
N
N 个样本，再写具体一点：
m
a
x
∑
i
=
1
N
u
T
(
x
i
x
i
T
)
u
，
且
∣
∣
u
∣
∣
=
1
max \sum_{i=1}^Nu^T(x_ix_i^T)u，且 ||u|| = 1
maxi=1∑NuT(xixiT)u，且∣∣u∣∣=1
求带约束条件的极值，我们用拉格朗日乘数法
L
(
u
,
λ
)
=
u
T
(
x
x
T
)
u
+
λ
(
1
−
u
T
u
)
L(u,\lambda) = u^T(xx^T)u+\lambda(1-u^Tu)
L(u,λ)=uT(xxT)u+λ(1−uTu)
分别对 u u u 和 λ \lambda λ 求偏导，令偏导为 0 求极值
∂ L ∂ u = 0 ⇒ 2 x x T u − 2 λ u = 0 ⇒ x x T u = λ u \frac{\partial L}{\partial u} = 0 \Rightarrow 2xx^Tu-2\lambda u = 0 \Rightarrow xx^Tu = \lambda u ∂u∂L=0⇒2xxTu−2λu=0⇒xxTu=λu
∂ L ∂ λ = 0 ⇒ 1 − u T u = 0 ⇒ u T u = 1 \frac{\partial L}{\partial \lambda} = 0 \Rightarrow 1-u^Tu = 0 \Rightarrow u^Tu = 1 ∂λ∂L=0⇒1−uTu=0⇒uTu=1
总结一下：
{
x
x
T
u
=
λ
u
u
T
u
=
1
\left\{\begin{matrix} xx^Tu = \lambda u \\ u^Tu = 1 \end{matrix}\right.
{xxTu=λuuTu=1
显然我们要求解的 u u u （投影方向） 是 x x T xx^T xxT 矩阵特征向量（单位化） ， λ \lambda λ 则是特征值！
2 最大方差
未完待续
扫一扫
892
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
