题目:
# P10789 [NOI2024] 登山
## 题目描述
“为什么要攀登?因为山就在那里。”
慕士塔格山上有 $n$ 处点位,点从 $1$ 到 $n$ 编号,$1$ 号点位为山顶。这 $n$ 个点位构成一棵有根树的结构,其中 $1$ 号点位为根,对于 $2\leq i\leq n$,$i$ 号点位的父亲结点为 $p_i$ 号点位。
记 $d_i$ 为 $i$ 号点位到山顶所需经过的边数。形式化地说,$d_1=0$,对于 $2\leq i\leq n$,$d_i=d_{p_i}+1$。
定义一条**登山路径**为从 $2\sim n$ 号点位中的某一个开始,经过若干次**移动**后**到达山顶**的方案。
定义一次从 $i(2\leq i\leq n)$ 号点位出发的**移动**为以下两种方式之一:
1. 冲刺:在给定的冲刺范围 $[l_i,r_i]$ 内,选择一个正整数 $k$ 满足 $l_i\leq k\leq r_i$,向山顶移动 $k$ 步,即移动至 $i$ 号点位在有根树上的 $k$ 级父亲处。保证 $1\leq l_i\leq r_i\leq d_i$。
2. 休息:由于慕士塔格山地形陡峭,休息时会滑落到某一个儿子结点处。形式化地说,选择一个满足 $p_j=i$ 的 $j$,移动至到 $j$ 号点位。特别地,若 $i$ 号点位为有根树的叶子结点,则不存在满足 $p_j=i$ 的 $j$,因此此时不能选择休息。
定义一条**登山路径**对应的**登山序列**为初始点位以及每次移动到的点位所构成的序列。形式化地说,一条从 $x$ 号点位开始的**登山路径**对应的****登山序列****是一个点序列 $a_1=x,a_2,\dots,a_m=1$ 满足对于 $1\leq i<m$,$a_{i+1}$ 是 $a_i$ 的 $k(l_{a_i}\leq k\leq r_{a_i})$ 级祖先或 $p_{a_{i+1}}=a_i$。
为了保证每次冲刺都能更接近山顶,一条**合法的登山路径**需要满足:对于初始点位或某次移动到的点位 $i$,以后冲刺到的点位 $j$ 都必须满足 $d_j<d_i-h_i$,其中 $h_i$ 是一个给定的参数,保证 $0\leq h_i<d_i$。形式化地说,一条**合法的登山路径**对应的**登山序列** $a_1,a_2,\dots,a_m$ 需要满足:对于所有 $1\leq i<j\leq m$,若 $p_{a_j} \neq a_{j-1}$,则 $d_{a_j}<d_{a_i}-h_{a_i}$。
对于 $2\sim n$ 号所有点位,求从这些点位开始的**合法的登山路径**条数。两条**登山路径**不同当且仅当其对应的**登山序列**不同。由于答案可能较大,你只需要求出答案对 $998\,244\,353$ 取模后的结果。
## 输入格式
**本题有多组测试数据。**
输入的第一行包含一个整数 $c$,表示测试点编号。$c=0$ 表示该测试点为样例。
输入的第二行包含一个整数 $t$,表示测试数据组数。
接下来依次输入每组测试数据,对于每组测试数据:
输入的第一行包含一个整数 $n$,表示慕士塔格山的点位数量。
接下来 $n-1$ 行,第 $i-1(2\leq i\leq n)$ 行包含四个整数 $p_i,l_i,r_i,h_i$。保证 $1\leq p_i<i$,$1\leq l_i\leq r_i\leq d_i$,$0\leq h_i<d_i$。
## 输出格式
对于每组测试数据,输出一行 $n-1$ 个整数,分别表示从点位 $2\sim n$ 到达山顶的方案数对 $998\,244\,353$ 取模后的结果。
## 输入输出样例 #1
### 输入 #1
```
0
3
5
1 1 1 0
2 1 1 0
2 1 2 1
4 2 3 0
6
1 1 1 0
2 1 2 0
3 1 3 2
4 1 4 1
5 1 5 3
6
1 1 1 0
2 1 2 0
2 1 2 0
3 1 2 0
3 2 3 2
```
### 输出 #1
```
3 3 2 4
5 9 3 21 6
4 10 5 14 1
```
## 输入输出样例 #2
### 输入 #2
```
见 mountain2.in/ans
这个样例满足测试点 2,3 的约束条件
```
### 输出 #2
```
```
## 输入输出样例 #3
### 输入 #3
```
见 mountain3.in/ans
这个样例满足测试点 9 的约束条件
```
### 输出 #3
```
```
## 输入输出样例 #4
### 输入 #4
```
见 mountain4.in/ans
这个样例满足测试点 11,12 的约束条件
```
### 输出 #4
```
```
## 输入输出样例 #5
### 输入 #5
```
见 mountain5.in/ans
这个样例满足测试点 13 的约束条件
```
### 输出 #5
```
```
## 说明/提示
**【样例 1 解释】**
样例 $1$ 共包含三组测试数据。
对于第一组测试数据,慕士塔格山的点位结构如下:
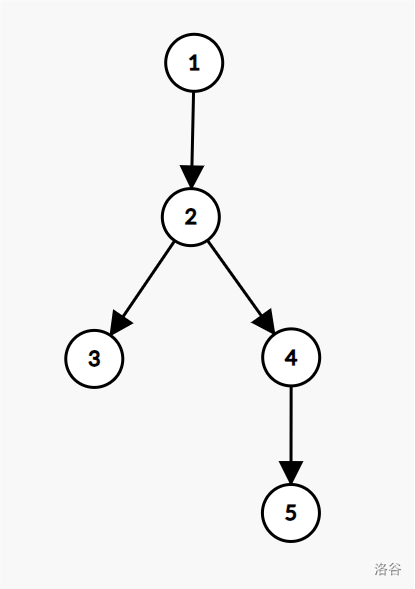
在该测试数据中,$d_1=0$,$d_2=1$,$d_3=d_4=2$,$d_5=3$。
从 $4$ 开始的合法的登山路径共有以下 $2$ 条:
1. 直接选择冲刺到 $4$ 的 $2$ 级父亲,也就是 $1$,到达山顶,对应的登山序列为 $[4,1]$。
2. 先休息滑落到 $5$,然后从 $5$ 冲刺到它的 $3$ 级父亲,到达山顶。对应的登山序列为 $[4,5,1]$。
从 $5$ 开始的合法的登山路径共有以下 $4$ 条:
1. 直接选择冲刺到 $5$ 的 $3$ 级父亲,也就是 $1$,到达山顶。对应的登山序列为 $[5,1]$。
2. 先冲刺到 $5$ 的 $2$ 级父亲,也就是 $2$;然后再从 $2$ 冲刺到它的 $1$ 级父亲,到达山顶。对应的登山序列为 $[5,2,1]$。
3. 先冲刺到 $5$ 的 $2$ 级父亲,也就是 $2$;然后在 $2$ 处休息,滑落到 $4$;接着从 $4$ 冲刺到它的 $2$ 级父亲,到达山顶。对应的登山序列为 $[5,2,4,1]$。
4. 先冲刺到 $5$ 的 $2$ 级父亲,也就是 $2$;然后在 $2$ 处休息,滑落到 $4$;继续休息,滑落到 $5$;接着从 $5$ 再次冲刺到它的 $3$ 级父亲,到达山顶。对应的登山序列为 $[5,2,4,5,1]$。
**【数据范围】**
对于所有测试数据保证:$1\leq t\leq 4$,$2\leq n\leq 10^5$。
对于任意的 $2\leq i\leq n$,保证:$1\leq p_i<i$,$1\leq l_i\leq r_i\leq d_i$,$0\leq h_i<d_i$。
| 测试点编号 | $n\leq$ | 是否有 $l_i=r_i$ | 是否有 $h_i=0$ | 是否有 $p_i=i-1$ |
| :----------: | :----------: | :----------: | :----------: | :----------: |
| $1$ | $6$ | 否 | 否 | 否 |
| $2,3$ | $300$ | 否 | 否 | 否 |
| $4,5$ | $5000$ | 否 | 否 | 否 |
| $6$ | $10^5$ | 是 | 是 | 是 |
| $7$ | $10^5$ | 是 | 是 | 否 |
| $8$ | $10^5$ | 是 | 否 | 是 |
| $9$ | $10^5$ | 是 | 否 | 否 |
| $10$ | $10^5$ | 否 | 是 | 是 |
| $11,12$ | $10^5$ | 否 | 是 | 否 |
| $13$ | $10^5$ | 否 | 否 | 是 |
| $14\sim 20$ | $10^5$ | 否 | 否 | 否 |
代码:
#include<bits/stdc++.h>
#define fi first
#define se second
using namespace std;
typedef pair<int,int> PII;
const int N=1e5+10;
const int mo=998244353;
int C,T,n,p[N],l[N],r[N],h[N];
int c[N],dp[N],d[N],st[N],cnt,S[N];
int dep[N],dfn[N],tim,siz[N];
int f[N][25],mn[N][25],lg[N];
int L[N],R[N],ff[N],lim[N],li[N];
vector<int> g[N],nxt[N];
vector<PII> q[N];
void update(int x,int y){while(x<=n)c[x]=(c[x]+y)%mo,x+=x&(-x);}
int query(int x){int res=0;while(x)res=(res+c[x])%mo,x-=x&(-x);return res;}
int query(int l,int r){return (query(r)-query(l-1))%mo;}
void init()
{
tim=0;
memset(c,0,sizeof(c));
for(int i=0;i<=n;i++) g[i].clear(),nxt[i].clear(),q[i].clear(),d[i]=0;
for(int i=2;i<=n;i++) dep[i]=dep[p[i]]+1,lim[i]=dep[i]-h[i]-1,L[i]=dep[i]-r[i],R[i]=dep[i]-l[i];
for(int i=2;i<=n;i++) f[i][0]=p[i],mn[i][0]=lim[p[i]];
for(int i=1;i<=n;i++) g[p[i]].push_back(i);
for(int j=1;j<=lg[n];j++)
for(int i=2;i<=n;i++)
f[i][j]=f[f[i][j-1]][j-1],mn[i][j]=min(mn[i][j-1],mn[f[i][j-1]][j-1]);
for(int i=2;i<=n;i++)
{
int v=i;
for(int j=lg[dep[i]];j>=0;j--)
if(f[v][j]&&mn[v][j]>=lim[i]) v=f[v][j];
ff[i]=p[v];nxt[ff[i]].push_back(i);
}
}
int kfa(int x,int k){return dep[x]<k?0:st[dep[x]-k+1];}
void dfs1(int u)
{
dfn[u]=++tim;siz[u]=1;
st[++cnt]=u;
li[u]=kfa(u,h[u]+1);
if(lim[u]>=L[u])
{
int v=u,kl=kfa(u,r[u]+1);
for(int i=lg[dep[u]];i>=0;i--)
if(f[v][i]&&mn[v][i]>=L[u]) v=f[v][i];
d[p[v]]--;
q[kl].push_back({u,-1});
q[kl].push_back({p[v],1});
}
else d[u]--;
if(lim[u]>R[u])
{
int v=u,kr=kfa(u,l[u]);
for(int i=lg[dep[u]];i>=0;i--)
if(f[v][i]&&mn[v][i]>R[u]) v=f[v][i];
d[p[v]]++;
q[kr].push_back({u,1});
q[kr].push_back({p[v],-1});
}
else d[u]++;
for(int v:g[u]) dfs1(v),siz[u]+=siz[v];
cnt--;
}
void dfs2(int u)
{
for(int v:nxt[u]) dfs2(v),d[u]+=d[v];
if(!u) return;
q[li[u]].push_back({u,d[u]});
q[li[u]].push_back({ff[u],-d[u]});
}
void DP(int u)
{
dp[u]=(u==1?1:query(dfn[u],dfn[u]+siz[u]-1));
S[u]=(S[p[u]]+dp[u])%mo;
for(auto v:q[u]) if(v.fi) update(dfn[v.fi],1ll*v.se*S[u]%mo);
for(int v:g[u]) DP(v);
}
int main()
{
for(int i=2;i<N;i++) lg[i]=lg[i>>1]+1;
scanf("%d%d",&C,&T);
while(T--)
{
scanf("%d",&n);
for(int i=2;i<=n;i++) scanf("%d%d%d%d",&p[i],&l[i],&r[i],&h[i]);
init();dfs1(1);dfs2(0);DP(1);
for(int i=2;i<=n;i++) printf("%d ",(dp[i]+mo)%mo);
printf("\n");
}
return 0;
}
为什么dfs2里面是访问 nxt 而不是 g 数组,答案才是对的,但是差分不是应该发生在树上的马























 311
311

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








