Golang每日一练(leetDay0087) 二叉树的最近公共祖先、最小子树

最新推荐文章于 2024-05-14 00:03:17 发布
原创 最新推荐文章于 2024-05-14 00:03:17 发布 · 422 阅读 · 8 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#golang #leetcode

文章介绍了二叉树中寻找两个指定节点最近公共祖先的两种方法，一种是迭代法，利用后序遍历和哈希表记录祖先节点；另一种是递归法，通过比较节点深度来找到最近公共祖先。此外，还讨论了包含所有最深节点的最小子树的问题，同样提供了迭代解法，寻找最深深度并返回包含这些节点的子树。

目录

236. 二叉树的最近公共祖先 Lowest Common Ancestor of a Binary-tree  🌟🌟

865. 具有所有最深节点的最小子树 Smallest-subtree-with-all-the-deepest-nodes  🌟🌟

1123. 最深叶节点的最近公共祖先 Lowest-common-ancestor-of-deepest-leaves​  🌟🌟

🌟 每日一练刷题专栏 🌟

Rust每日一练 专栏

Golang每日一练 专栏

Python每日一练 专栏

C/C++每日一练 专栏

Java每日一练 专栏

236. 二叉树的最近公共祖先 Lowest Common Ancestor of a Binary-tree

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

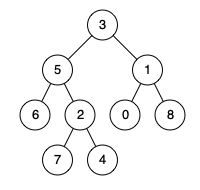
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

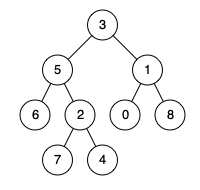
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。
因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

  • 树中节点数目在范围 [2, 10^5] 内。
  • -10^9 <= Node.val <= 10^9
  • 所有 Node.val 互不相同 。
  • p != q
  • p 和 q 均存在于给定的二叉树中。

代码1：迭代法

  • 使用栈将后序遍历改为迭代遍历，同时记录每个节点的父节点；
  • 找到 p 和 q 的所有祖先节点，并存储在一个 hash set 中；
  • 从 p 开始，不断向上查找，记录其祖先节点并存在另一个 hash set 中；
  • 从 q 开始向上查找祖先节点，如果已经在上一个 hash set 中存在，则找到了最近公共祖先节点。
package main

import (
	"fmt"
	"strings"
)

const null = -1 << 31

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func buildTree(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	root := &TreeNode{Val: nums[0]}
	Queue := []*TreeNode{root}
	idx := 1
	for idx < len(nums) {
		node := Queue[0]
		Queue = Queue[1:]
		if nums[idx] != null {
			node.Left = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Left)
		}
		idx++
		if idx < len(nums) && nums[idx] != null {
			node.Right = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Right)
		}
		idx++
	}
	return root
}

func levelOrder(root *TreeNode) [][]int {
	res := [][]int{}
	if root == nil {
		return res
	}
	Queue := []*TreeNode{root}
	for len(Queue) > 0 {
		level := []int{}
		n := len(Queue)
		for i := 0; i < n; i++ {
			cur := Queue[0]
			Queue = Queue[1:]
			level = append(level, cur.Val)
			if cur.Left != nil {
				Queue = append(Queue, cur.Left)
			}
			if cur.Right != nil {
				Queue = append(Queue, cur.Right)
			}
		}
		res = append(res, level)
	}
	return res
}

func Array2DToString(array [][]int) string {
	if len(array) == 0 {
		return "[]"
	}
	arr2str := func(arr []int) string {
		res := "["
		for i := 0; i < len(arr); i++ {
			res += fmt.Sprint(arr[i])
			if i != len(arr)-1 {
				res += ","
			}
		}
		return res + "]"
	}
	res := make([]string, len(array))
	for i, arr := range array {
		res[i] = arr2str(arr)
	}
	return strings.Join(strings.Fields(fmt.Sprint(res)), ",")
}

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
	parent := make(map[*TreeNode]*TreeNode)
	stack := []*TreeNode{root}

	for len(stack) > 0 {
		node := stack[len(stack)-1]
		stack = stack[:len(stack)-1]

		if node.Left != nil {
			parent[node.Left] = node
			stack = append(stack, node.Left)
		}

		if node.Right != nil {
			parent[node.Right] = node
			stack = append(stack, node.Right)
		}
	}

	ancestors := make(map[*TreeNode]bool)
	for p != nil {
		ancestors[p] = true
		p = parent[p]
	}

	for q != nil {
		if ancestors[q] {
			return q
		}
		q = parent[q]
	}

	return nil
}

func main() {
	nums := []int{3, 5, 1, 6, 2, 0, 8, null, null, 7, 4}
	root := buildTree(nums)
	p, q := root.Left, root.Right
	fmt.Println(Array2DToString(levelOrder(root)))
	fmt.Println(lowestCommonAncestor(root, p, q).Val)

	q = root.Left.Right.Right
	fmt.Println(lowestCommonAncestor(root, p, q).Val)

	nums = []int{1, 2}
	root = buildTree(nums)
	p, q = root, root.Left
	fmt.Println(Array2DToString(levelOrder(root)))
	fmt.Println(lowestCommonAncestor(root, p, q).Val)
}

代码2： 递归法

  • 如果当前节点为 nil 或者等于 p 或 q 中的任意一个，则返回当前节点；
  • 在左子树中查找是否包含 p 或 q，返回值为 l；
  • 在右子树中查找是否包含 p 或 q，返回值为 r；
  • a) 如果 l 和 r 都不为空，说明 p 和 q 分别在当前节点的左右子树，则当前节点就是它们的最近公共祖先节点；
    b) 如果 l 为空，说明 p 和 q 都在右子树中，则最近公共祖先节点一定在右子树中，返回 r；
    c) 如果 r 为空，说明 p 和 q 都在左子树中，则最近公共祖先节点一定在左子树中，返回 l。
package main

import (
	"fmt"
	"strings"
)

const null = -1 << 31

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func buildTree(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	root := &TreeNode{Val: nums[0]}
	Queue := []*TreeNode{root}
	idx := 1
	for idx < len(nums) {
		node := Queue[0]
		Queue = Queue[1:]
		if nums[idx] != null {
			node.Left = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Left)
		}
		idx++
		if idx < len(nums) && nums[idx] != null {
			node.Right = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Right)
		}
		idx++
	}
	return root
}

func levelOrder(root *TreeNode) [][]int {
	res := [][]int{}
	if root == nil {
		return res
	}
	Queue := []*TreeNode{root}
	for len(Queue) > 0 {
		level := []int{}
		n := len(Queue)
		for i := 0; i < n; i++ {
			cur := Queue[0]
			Queue = Queue[1:]
			level = append(level, cur.Val)
			if cur.Left != nil {
				Queue = append(Queue, cur.Left)
			}
			if cur.Right != nil {
				Queue = append(Queue, cur.Right)
			}
		}
		res = append(res, level)
	}
	return res
}

func Array2DToString(array [][]int) string {
	if len(array) == 0 {
		return "[]"
	}
	arr2str := func(arr []int) string {
		res := "["
		for i := 0; i < len(arr); i++ {
			res += fmt.Sprint(arr[i])
			if i != len(arr)-1 {
				res += ","
			}
		}
		return res + "]"
	}
	res := make([]string, len(array))
	for i, arr := range array {
		res[i] = arr2str(arr)
	}
	return strings.Join(strings.Fields(fmt.Sprint(res)), ",")
}

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
	if root == nil || root.Val == p.Val || root.Val == q.Val {
		return root
	}

	l := lowestCommonAncestor(root.Left, p, q)
	r := lowestCommonAncestor(root.Right, p, q)

	if l != nil && r != nil { // postorder
		return root
	} else if l == nil {
		return r
	} else {
		return l
	}
}

func main() {
	nums := []int{3, 5, 1, 6, 2, 0, 8, null, null, 7, 4}
	root := buildTree(nums)
	p, q := root.Left, root.Right
	fmt.Println(Array2DToString(levelOrder(root)))
	fmt.Println(lowestCommonAncestor(root, p, q).Val)

	q = root.Left.Right.Right
	fmt.Println(lowestCommonAncestor(root, p, q).Val)

	nums = []int{1, 2}
	root = buildTree(nums)
	p, q = root, root.Left
	fmt.Println(Array2DToString(levelOrder(root)))
	fmt.Println(lowestCommonAncestor(root, p, q).Val)
}

输出：

[[3],[5,1],[6,2,0,8],[7,4]]

3

5

[[1],[2]]

1

865. 具有所有最深节点的最小子树 Smallest-subtree-with-all-the-deepest-nodes

给定一个根为 root 的二叉树，每个节点的深度是 该节点到根的最短距离 。

返回包含原始树中所有 最深节点 的 最小子树 。

如果一个节点在 整个树 的任意节点之间具有最大的深度，则该节点是 最深的 。

一个节点的 子树 是该节点加上它的所有后代的集合。

示例 1：

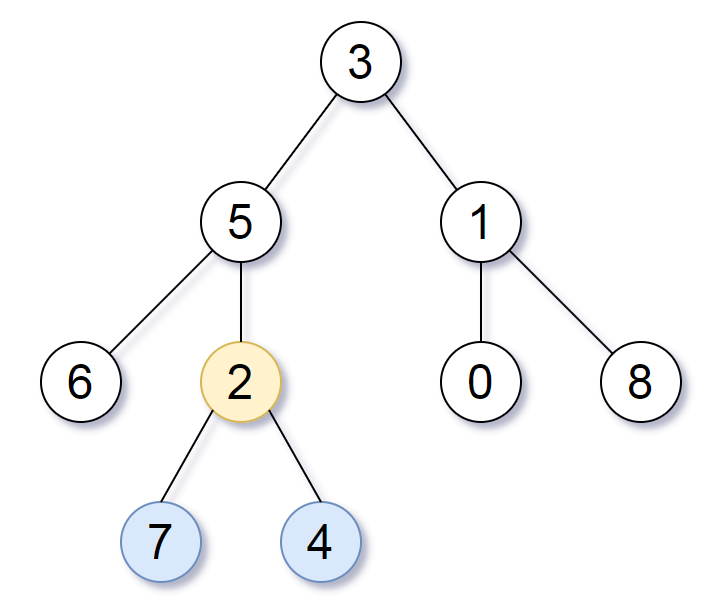
输入：root = [3,5,1,6,2,0,8,null,null,7,4]
输出：[2,7,4]
解释：
我们返回值为 2 的节点，在图中用黄色标记。
在图中用蓝色标记的是树的最深的节点。
注意，节点 5、3 和 2 包含树中最深的节点，但节点 2 的子树最小，因此我们返回它。

示例 2：

输入：root = [1]
输出：[1]
解释：根节点是树中最深的节点。

示例 3：

输入：root = [0,1,3,null,2]
输出：[2]
解释：树中最深的节点为 2 ，有效子树为节点 2、1 和 0 的子树，但节点 2 的子树最小。

提示：

  • 树中节点的数量在 [1, 500] 范围内。
  • 0 <= Node.val <= 500
  • 每个节点的值都是 独一无二 的。

注意：本题与力扣 1123 重复

代码：迭代法

  • 使用栈将前序遍历改为迭代遍历，同时记录每个节点的深度；
  • 找到树中所有最深节点的深度；
  • 从根节点开始，不断向下查找，遇到最深深度的节点就返回。
package main

import (
	"fmt"
	"strings"
)

const null = -1 << 31

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func buildTree(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	root := &TreeNode{Val: nums[0]}
	Queue := []*TreeNode{root}
	idx := 1
	for idx < len(nums) {
		node := Queue[0]
		Queue = Queue[1:]
		if nums[idx] != null {
			node.Left = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Left)
		}
		idx++
		if idx < len(nums) && nums[idx] != null {
			node.Right = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Right)
		}
		idx++
	}
	return root
}

func levelOrder(root *TreeNode) [][]int {
	res := [][]int{}
	if root == nil {
		return res
	}
	Queue := []*TreeNode{root}
	for len(Queue) > 0 {
		level := []int{}
		n := len(Queue)
		for i := 0; i < n; i++ {
			cur := Queue[0]
			Queue = Queue[1:]
			level = append(level, cur.Val)
			if cur.Left != nil {
				Queue = append(Queue, cur.Left)
			}
			if cur.Right != nil {
				Queue = append(Queue, cur.Right)
			}
		}
		res = append(res, level)
	}
	return res
}

func Array2DToString(array [][]int) string {
	if len(array) == 0 {
		return "[]"
	}
	arr2str := func(arr []int) string {
		res := "["
		for i := 0; i < len(arr); i++ {
			res += fmt.Sprint(arr[i])
			if i != len(arr)-1 {
				res += ","
			}
		}
		return res + "]"
	}
	res := make([]string, len(array))
	for i, arr := range array {
		res[i] = arr2str(arr)
	}
	return strings.Join(strings.Fields(fmt.Sprint(res)), ",")
}

func subtreeWithAllDeepest(root *TreeNode) *TreeNode {
	depth := make(map[*TreeNode]int)
	stack := []*TreeNode{root}
	maxDepth := -1
	if root.Left == nil && root.Right == nil {
		return root
	}
	for len(stack) > 0 {
		node := stack[len(stack)-1]
		stack = stack[:len(stack)-1]

		if node.Left != nil {
			depth[node.Left] = depth[node] + 1
			stack = append(stack, node.Left)
		}

		if node.Right != nil {
			depth[node.Right] = depth[node] + 1
			stack = append(stack, node.Right)
		}
	}

	for _, d := range depth {
		if d > maxDepth {
			maxDepth = d
		}
	}

	return dfs(root, depth, maxDepth)
}

func dfs(node *TreeNode, depth map[*TreeNode]int, maxDepth int) *TreeNode {
	if node == nil {
		return nil
	}

	if depth[node] == maxDepth {
		return node
	}

	left := dfs(node.Left, depth, maxDepth)
	right := dfs(node.Right, depth, maxDepth)

	if left != nil && right != nil {
		return node
	} else if left == nil {
		return right
	} else {
		return left
	}
}

func main() {
	nums := []int{3, 5, 1, 6, 2, 0, 8, null, null, 7, 4}
	root := buildTree(nums)
	fmt.Println(Array2DToString(levelOrder(root)))
	res := subtreeWithAllDeepest(root)
	fmt.Println(Array2DToString(levelOrder(res)))

	nums = []int{1}
	root = buildTree(nums)
	fmt.Println(Array2DToString(levelOrder(root)))
	res = subtreeWithAllDeepest(root)
	fmt.Println(Array2DToString(levelOrder(res)))

	nums = []int{0, 1, 3, null, 2}
	root = buildTree(nums)
	fmt.Println(Array2DToString(levelOrder(root)))
	res = subtreeWithAllDeepest(root)
	fmt.Println(Array2DToString(levelOrder(res)))

}

输出：

[[3],[5,1],[6,2,0,8],[7,4]]

[[2],[7,4]]

[[1]]

[[1]]

[[0],[1,3],[2]]

[[2]]

1123. 最深叶节点的最近公共祖先 Lowest-common-ancestor-of-deepest-leaves​

给你一个有根节点 root 的二叉树，返回它 最深的叶节点的最近公共祖先 。

回想一下：

  • 叶节点 是二叉树中没有子节点的节点
  • 树的根节点的 深度 为 0，如果某一节点的深度为 d，那它的子节点的深度就是 d+1
  • 如果我们假定 A 是一组节点 S 的 最近公共祖先，S 中的每个节点都在以 A 为根节点的子树中，且 A 的深度达到此条件下可能的最大值。

示例 1：

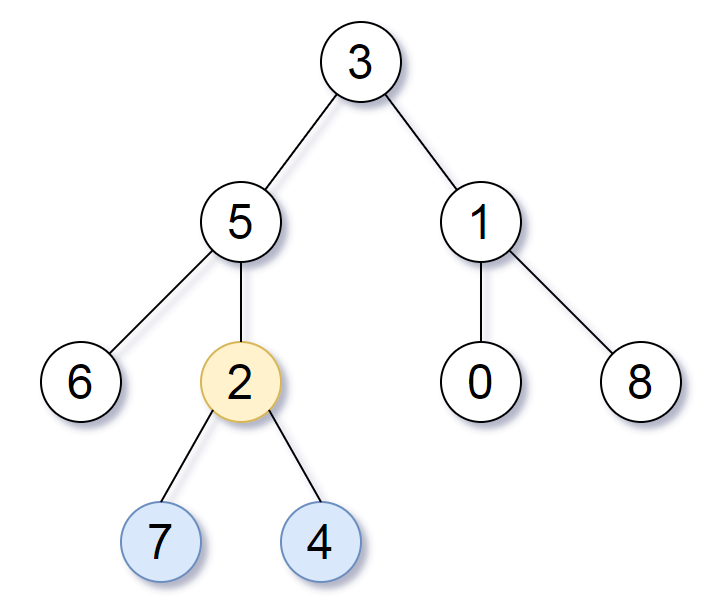
输入：root = [3,5,1,6,2,0,8,null,null,7,4]
输出：[2,7,4]
解释：我们返回值为 2 的节点，在图中用黄色标记。
在图中用蓝色标记的是树的最深的节点。
注意，节点 6、0 和 8 也是叶节点，但是它们的深度是 2 ，而节点 7 和 4 的深度是 3 。

示例 2：

输入：root = [1]
输出：[1]
解释：根节点是树中最深的节点，它是它本身的最近公共祖先。

示例 3：

输入：root = [0,1,3,null,2]
输出：[2]
解释：树中最深的叶节点是 2 ，最近公共祖先是它自己。

提示：

  • 树中的节点数将在 [1, 1000] 的范围内。
  • 0 <= Node.val <= 1000
  • 每个节点的值都是 独一无二 的。

注意：本题与力扣 865 重复

🌟 每日一练刷题专栏 🌟

✨ 持续，努力奋斗做强刷题搬运工！

👍 点赞，你的认可是我坚持的动力！ 

🌟 收藏，你的青睐是我努力的方向！ 

✎ 评论，你的意见是我进步的财富！  

☸ 主页：https://hannyang.blog.youkuaiyun.com/ 

Rust每日一练 专栏

（2023.5.16~）更新中...

Golang每日一练 专栏

（2023.3.11~）更新中...

Python每日一练 专栏

（2023.2.18~2023.5.18）暂停更

C/C++每日一练 专栏

（2023.2.18~2023.5.18）暂停更

Java每日一练 专栏

（2023.3.11~2023.5.18）暂停更

LeetCode 0235.二叉搜索树的最近公共祖先【Go】
笔记|思路|总结
01-04 166
LeetCode 0235.二叉搜索树的最近公共祖先
LeetCode 0236.二叉树的最近公共祖先【Go】
笔记|思路|总结
01-04 469
LeetCode 0236.二叉树的最近公共祖先
【二叉树算法】golang-最近公共祖先问题
weixin_41198062的博客
05-10 356
二叉树最近公共祖先问题 一般二叉树 常规二叉树无序，故需使用回溯方式，自底向上遍历整棵树，找到符合条件的节点 // 二叉树的最近公共祖先 func findNearAncestor(node, p, q *TreeNode) *TreeNode { // 从叶子节点向上遍历整个二叉树 return checkInNode(node, p, q) } func checkInNode(node, p, q *TreeNode) *TreeNode { if node == p || node ==
二叉搜索树的最近公共祖先——递归/非递归
weixin_45594172的博客
10-02 1008
二叉搜索树的最近公共祖先——递归/非递归
二叉搜索树的最近公共祖先的golang实现
12-17 420
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。” 例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5] 输入: root =...
235. 二叉搜索树的最近公共祖先
WhiteGray的博客
09-27 158
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。” 例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5] 示例 1: 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点 2
【二叉树算法】golang--构造二叉树
weixin_41198062的博客
04-29 1236
构造二叉树 算法逻辑 从前序或后序数组中，找到根节点Val值，对应为第一个元素或最后一个元素 以根节点为切割点，分割中序数组、前/后序数组，注意先分割中序 递归方式，得到最终结果 疑问：为什么要递归 当将数组分为左子树Val和右子树Val值后，后面的步骤和之前是完全一致的。 均为找到根节点，分割左右子树 所以采用递归方式 通过前序遍历和中序遍历数组构造二叉树 // 通过前序遍历和中序遍历构造二叉树 func buildBinaryTreeII(preorder, inorder []int) *T
2024年Go最全【数据结构】平衡二叉树的插入、删除_平衡二叉树插入怎么插，Golang内存优化面试题
最新发布
2401_84911119的博客
05-14 1015
else if(key == t.value) //找到元素结点。else if(key == t.value) //找到元素结点。if(t.lchild == null) //左子树为空。if(t.lchild == null) //左子树为空。if(t.lchild.bf == EH) //注意这里，画图思考一下。
【go从入门到精通】Golang 中最常见的 5 个错误
热门推荐
网易搬砖头
04-18 4万+
本文重点介绍了 Golang 中最常见的五个错误，并提供了每个错误的示例以及如何纠正这些错误。继续编码，从错误中学习，并探索 Go 提供的丰富功能和便利。使用通道时，确保发送和接收正确平衡，并且它们并行发生，通常在不同的 Goroutines 中。一个常见的错误是手动处理资源清理，这可能会导致问题，尤其是在清理之前发生错误时。在 Go 中，当一个类型实现了接口所需的所有方法时，就满足了接口的要求。Go 中的一个常见错误是没有正确实现接口，这通常是由于对 Go 中如何隐式满足接口的误解所致。
【Go语言实战】(23)封装一个加密包，让敏感数据更易脱敏 【 Golang | Go语言】
面向生活编程
10-12 2133
提供 对称加密 AES、DES、3DES 以及非对称加密 RSA 的上层封装接口，让您的敏感数据更加容易脱敏并存储
LeetCode 236. 二叉树的最近公共祖先Golang版
菜到不敢run
03-22 426
LeetCode 236. 二叉树的最近公共祖先Golang版 1. 问题描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。” 2. 思路 确定递归函数参数和返回值 func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode 确定终止条件
NC102 在二叉树中找到两个节点的最近公共祖先（Golang）
Hello_Bye的博客
01-09 456
package main import . "nc_tools" /* * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ /** * * @param root TreeNode类 * @param o1 int整型 * @param o2 int整型 * @return int整型 */ func lowestCommonAncestor( root *Tre
236.二叉树的最近公共祖先
qq_40058686的博客
02-23 166
该题也是利用了后续遍历的思想，遍历顺序为左子树，右子树，根节点。假如该节点为公共祖先节点，那么p，q一定都是该节点的子节点。不过因为这里是最近公共祖先，有个最近，则不能是两个子节点的祖先的祖先，所以就用到了后序遍历，只有有左节点，则一直找下去，找不到再回溯到上一节点。如果满足条件了，则直接更新结果为这个节点，这样就能保证找到的都是最近公共祖先节点了。只需要判断当前节点，左节点，右节点中是否满足条件...
[leetcode]236. Lowest Common Ancestor of a Binary Tree树的最小公共祖先
weixin_30235225的博客
01-26 130
如果一个节点的左右子树上分别有两个节点，那么这棵树是祖先，但是不一定是最小的，但是从下边开始判断，找到后一直返回到上边就是最小的。 如果一个节点的左右子树上只有一个子树上遍历到了节点，那么那个子树可能是一个节点的祖先，也可能是两个节点的祖先，如果是一个节点的祖先，那么公共祖先还在上边，还需要返回结果进行判断，如果是两个节点的祖先，那么最小公共祖先就是这个或者在下边，总之，返回有结果的那...
LeetCode0236.二叉树的最近公共祖先 Go语言AC笔记
Hexa_H的博客
10-22 236
用后序遍历的方法通知父节点寻找最近公共祖先。
求两个树结点的最低公共祖先（Again）
Poem~
09-29 1184
题目：输入两个树结点，求它们的最低公共祖先。 事实上，这是一组题目， 情况一：此树为二叉树，且为二叉搜索树; 二叉搜索树是排过序的，位于左子树的结点都比父节点小；位于右子树的结点都比右子树大，我们只需要从树的根节点开始和两个输入的结点进行比较，如果当前结点的值比两个结点的值都要大，那么最低公共父节点一定在当前结点的左子树中，于是下一步遍历当前结点的左子树。如果当前结点的值比两个结点的值都小，
LeetCode 具有所有最深节点的最小子树（递归）
hestyle的博客
06-08 1062
给定一个根为 root 的二叉树，每个结点的深度是它到根的最短距离。 如果一个结点在整个树的任意结点之间具有最大的深度，则该结点是最深的。 一个结点的子树是该结点加上它的所有后代的集合。 返回能满足“以该结点为根的子树中包含所有最深的结点”这一条件的具有最大深度的结点。 示例： 输入：[3,5,1,6,2,0,8,null,null,7,4] 输出：[2,7,4] 解释： 我们返回值为 2 的...
求公共子树（后缀树法）
Bro_Bear的博客
03-29 1921
内容来自 晁晓菲,杨晓龙,李书琴,唐晶磊.两棵树的公共子树查找算法综述[J].陕西理工学院学报(自然科学版),2009,25(02):33-39. 求公共子树 后缀树法-Grossi 后缀树 BANANA的后缀 其中叶子节点的数字代表该后缀的在原字符串中的起始坐标 基本步骤 将树结构转化为编码，将两个编码拼接，根据拼接编码构造后缀树 查找公共后缀，找到公共子树 1 构造后缀树 1.1 前...
二叉搜索树的最近公共祖先
Learner_QUN的博客
05-08 576
因为是有序树，所有 如果 中间节点是 q 和 p 的公共祖先，那么 中节点的数组 一定是在 [p, q]区间的。如图，我们从根节点搜索，第一次遇到 cur节点是数值在[p, q]区间中，即 节点5，此时可以说明 p 和 q 一定分别存在于 节点 5的左子树，和右子树中。在搜索二叉树的公共祖先时，利用回溯从底向上搜索，遇到一个节点的左子树里有p，右子树里有q，那么当前节点就是最近公共祖先。所以当我们从上向下去递归遍历，第一次遇到 cur节点是数值在[p, q]区间中，那么cur就是 p和q的最近公共祖先。
golang 每日一库
07-28
Golang每日一库是一个系列的文章，旨在介绍Golang中的各种优秀的第三方库。其中一篇文章介绍了zap库和logrus库。\[1\]zap库是Golang中性能最高的日志库，而logrus库虽然已经不再维护和更新，但在使用的简易程度方面更好用一些。\[1\]除了这两个库，还有很多其他的日志库可以选择。另外，flag库也是Golang中常用的库之一，用于处理命令行参数。\[2\]\[3\]flag库提供了多种选项类型，包括自定义选项类型和时间间隔类型。自定义选项类型可以根据需求进行定义，而时间间隔类型支持多种格式，如"300ms"、"-1.5h"、"2h45m"等。\[2\]\[3\]这些库都是Golang开发中常用的工具，可以帮助开发者更高效地进行日志记录和命令行参数处理。 #### 引用[.reference_title] - *1* [Golang一日一库之logrus](https://blog.youkuaiyun.com/Zuko_chen/article/details/130212672)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip_chatgpt_common_search_pc_result","utm_medium":"distribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v91^insert_down28v1,239^v3^insert_chatgpt"}} ] [.reference_item] - *2* *3* [Go每日一库之Flag](https://blog.youkuaiyun.com/weixin_43999327/article/details/130701461)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip_chatgpt_common_search_pc_result","utm_medium":"distribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v91^insert_down28v1,239^v3^insert_chatgpt"}} ] [.reference_item] [ .reference_list ]
评论 4
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

Hann Yang

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值