Python 二叉树相关术语及力扣真题操练_python 树考试题-优快云博客

文章介绍了二叉树的基本概念，包括节点、度、叶子节点等术语，并阐述了二叉树的五种基本形态。通过LeetCode真题展示了如何判断两棵树是否相同以及如何翻转二叉树。此外，还讨论了平衡二叉树的判断方法，提供了解决相关问题的代码实现。

二叉树

Binarytree 是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分。
二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个节点。

二叉树（binarytree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。

二叉树是递归定义的，其节点有左右子树之分，逻辑上二叉树有五种基本形态：
1、空二叉树；2、只有一个根节点的二叉树；3、只有左子树；4、只有右子树；5、完全二叉树。

常用术语

①节点：包含一个数据元素及若干指向子树分支的信息。
②节点的度：一个节点拥有子树的数目称为节点的度。
③叶子节点：也称为终端节点，没有子树的节点或者度为零的节点。
④分支节点：也称为非终端节点，度不为零的节点称为非终端节点。
⑤树的度：树中所有节点的度的最大值。
⑥节点的层次：从根节点开始，假设根节点为第1层，根节点的子节点为第2层，依此类推，如果某一个节点位于第L层，则其子节点位于第L+1层。
⑦树的深度：也称为树的高度，树中所有节点的层次最大值称为树的深度。
⑧有序树：如果树中各棵子树的次序是有先后次序，则称该树为有序树。
⑨无序树：如果树中各棵子树的次序没有先后次序，则称该树为无序树。
⑩森林：由m（m≥0）棵互不相交的树构成一片森林。如果把一棵非空的树的根节点删除，则该树就变成了一片森林，森林中的树由原来根节点的各棵子树构成。

leetcode真题操练

相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

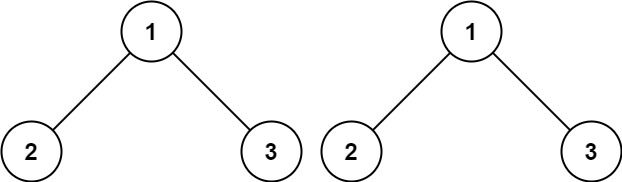
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

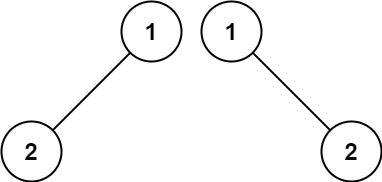
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

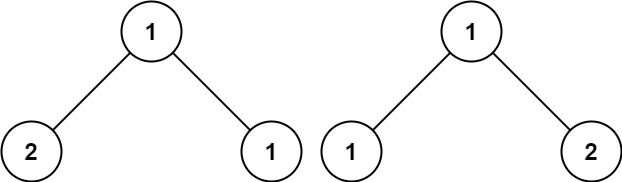
输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

两棵树上的节点数目都在范围 [0, 100] 内
-10^4 <= Node.val <= 10^4

代码：

class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution(object):
    def isSameTree(self, p, q):
        """
        :type p: TreeNode
        :type q: TreeNode
        :rtype: bool
        """
        if p == q:
            return True
        try:
            left = right = True
            if p.val == q.val:
                left = self.isSameTree(p.left, q.left)
                right = self.isSameTree(p.right, q.right)
                return (left and right)
        except:
            return False
        return False

# %%
s = Solution()
print(s.isSameTree(p = [1,2,3], q = [1,2,3]))

print(s.isSameTree(p = [1,2], q = [1,None,2]))
print(s.isSameTree(p = [1,2,1], q = [1,1,2]))

输出：

True
False
False

翻转二叉树

翻转一棵二叉树。

示例 1：

输入：

     4
   /   \
  2     7
 / \   / \
1   3 6   9

输出：

     4
   /   \
  7     2
 / \   / \
9   6 3   1

示例 2：

输入：

          1
        /   \
       2     3
      /     / \
     4     5   6
                \
                 7

输出：

          1
        /   \
       3     2
      / \     \
     6   5     4
    /
   7

代码：

class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

class Solution(object):
    def invertTree(self, root):
        """
        :type root: TreeNode
        :rtype: TreeNode
        """
        if not root:
            return None
        root.left, root.right = root.right, root.left
        self.invertTree(root.left)
        self.invertTree(root.right)
        return root

def listToTree(lst: list) -> TreeNode:
    if not lst:
        return None
    root = TreeNode(lst[0])
    queue = [root]
    i = 1
    while i < len(lst):
        node = queue.pop(0)
        if lst[i] is not None:
            node.left = TreeNode(lst[i])
            queue.append(node.left)
        i += 1
        if i < len(lst) and lst[i] is not None:
            node.right = TreeNode(lst[i])
            queue.append(node.right)
        i += 1
    return root

def inorderTraversal(root: TreeNode) -> list:
    if not root:
        return []
    res = []
    res += inorderTraversal(root.left)
    res.append(root.val)
    res += inorderTraversal(root.right)
    return res

# %%
s = Solution()

lst = [4, 2, 7, 1, 3, 6, 9]
root = listToTree(lst)
print(inorderTraversal(root))
root = s.invertTree(root)
print(inorderTraversal(root))

lst = [1, 2, 3, 4, None, 5, 6, None, None, None, None, None, 7]
root = listToTree(lst)
print(inorderTraversal(root))
root = s.invertTree(root)
print(inorderTraversal(root))

输出：

[1, 2, 3, 4, 6, 7, 9]
[9, 7, 6, 4, 3, 2, 1]
[4, 2, 1, 5, 3, 6, 7]
[7, 6, 3, 5, 1, 2, 4]

翻转二叉树的非递归实现：

def invertTree(root: TreeNode) -> TreeNode:
if not root:
return None
stack = [root]
while stack:
node = stack.pop()
if node:
node.left, node.right = node.right, node.left
stack.append(node.left)
stack.append(node.right)
return root

平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

树中的节点数在范围 [0, 5000] 内
-10^4 <= Node.val <= 10^4

出处：

https://edu.youkuaiyun.com/practice/26912046

代码：

# 定义二叉树节点
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution(object):
    def isBalanced(self, root):
        if not root:
            return True
        left_depth = self.get_depth(root.left)
        right_depth = self.get_depth(root.right)
        if abs(left_depth - right_depth) > 1:
            return False
        else:
            return self.isBalanced(root.left) and self.isBalanced(root.right)
    def get_depth(self, root):
        if root is None:
            return 0
        else:
            return max(self.get_depth(root.left), self.get_depth(root.right)) + 1

def listToTree(lst):
    if not lst:
        return None
    root = TreeNode(lst[0])
    queue = [root]
    i = 1
    while i < len(lst):
        node = queue.pop(0)
        if lst[i] is not None:
            node.left = TreeNode(lst[i])
            queue.append(node.left)
        i += 1
        if i < len(lst) and lst[i] is not None:
            node.right = TreeNode(lst[i])
            queue.append(node.right)
        i += 1
    return root

# %%
s = Solution()
null = None
nums = [3,9,20,null,null,15,7]
root = listToTree(nums)
print(s.isBalanced(root))
nums = [1,2,2,3,3,null,null,4,4]
root = listToTree(nums)
print(s.isBalanced(root))

输出：

True
False

二叉树的右视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2:

输入: [1,null,3]
输出: [1,3]

示例 3:

输入: []
输出: []

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

代码：

class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

def listToTree(lst: list) -> TreeNode:
    if not lst:
        return None
    root = TreeNode(lst[0])
    queue = [root]
    i = 1
    while i < len(lst):
        node = queue.pop(0)
        if lst[i] is not None:
            node.left = TreeNode(lst[i])
            queue.append(node.left)
        i += 1
        if i < len(lst) and lst[i] is not None:
            node.right = TreeNode(lst[i])
            queue.append(node.right)
        i += 1
    return root

def inorderTraversal(root: TreeNode) -> list:
    if not root:
        return []
    res = []
    res += inorderTraversal(root.left)
    res.append(root.val)
    res += inorderTraversal(root.right)
    return res
  
def rightSideView(root: TreeNode) -> list:
    if not root:
        return []

    result = []
    queue = [root]

    while queue:
        size = len(queue)
        for i in range(size):
            node = queue.pop(0)
            if i == size - 1:  # 最右边的节点
                result.append(node.val)

            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)

    return result
  

# %%
null = None
node = [1,2,3,null,5,null,4]
root = listToTree(node)  
print(rightSideView(root))

node = [1,null,3]
root = listToTree(node)  
print(rightSideView(root))

输出：
[1, 3, 4]
[1, 3]