Python 机器人魔鬼的步伐中居然隐藏着杨辉三角形

最新推荐文章于 2024-04-12 10:43:41 发布

原创最新推荐文章于 2024-04-12 10:43:41 发布 · 967 阅读

20 ·

CC 4.0 BY-SA版权

Python 专栏收录该内容

215 篇文章

订阅专栏

本文探讨了LeetCode第62题的解决方案，揭示了机器人移动路径与杨辉三角的关系，并提供了多种计算走法的算法，包括递归、组合公式和优化的动态规划方法。同时扩展到了有障碍物的地图，讨论了路径计数的变化。

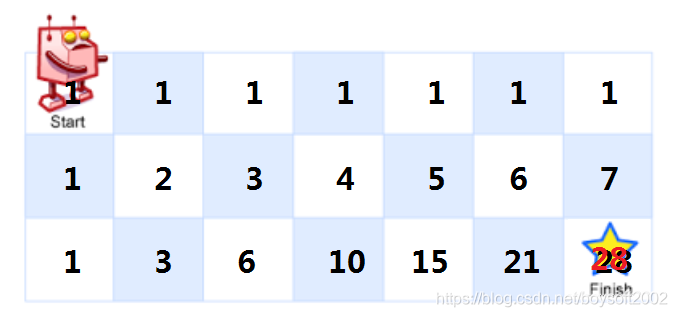
机器人位于如下图 m x n网格的左上角，通过移动到达网格的右下角。但它的每次移动只能是向下或者向右移动一格，请问从起点到终点共有多少种走法？

问题来自于leetcode第62号题目，经过深入地摸索发现，在这个机器人的魔性步伐里居然隐藏着一个“杨辉三角形”。先来看看，如何解决这个第62题：

方法一：很明显，机器人到达地图上第一行或者第一列的任一点，都只有1种走法；第2行竟然就是一个自然数数列 1,2,3,4,.... ；到第3行发现第二格开始每一格都是前一格与上一格的和。于是用数学归纳法推断出一个结论：任意点的走法数是 map[i][j] = map[i-1][j] + map[i][j-1] ，i>0,j>0；map[0][j]=map[i][0]=1。

代码如下：

>>> def paths(m,n):
	map = [[1 for _ in range(n)] for _ in range(m)]
	for i in range(1,m):
		for j in range(1,n):
			map[i][j] = map[i-1][j] + map[i][j-1]
	return map[m-1][n-1]

>>> m,n = 2,3
>>> paths(m,n)
3
>>> m,n = 3,3
>>> paths(m,n)
6
>>> m,n = 3,7
>>> paths(m,n)
28
>>>

改进代码：

def paths2(m,n):
	if m<n: m,n=n,m
	map = [[1]*m for _ in range(n)]
	map[1] = [i+1 for i in range(m)]
	for i in range(2,n):
		for j in range(1,m):
			map[i][j] = map[i][j-1]+map[i-1][j]
	return map[-1][-1]

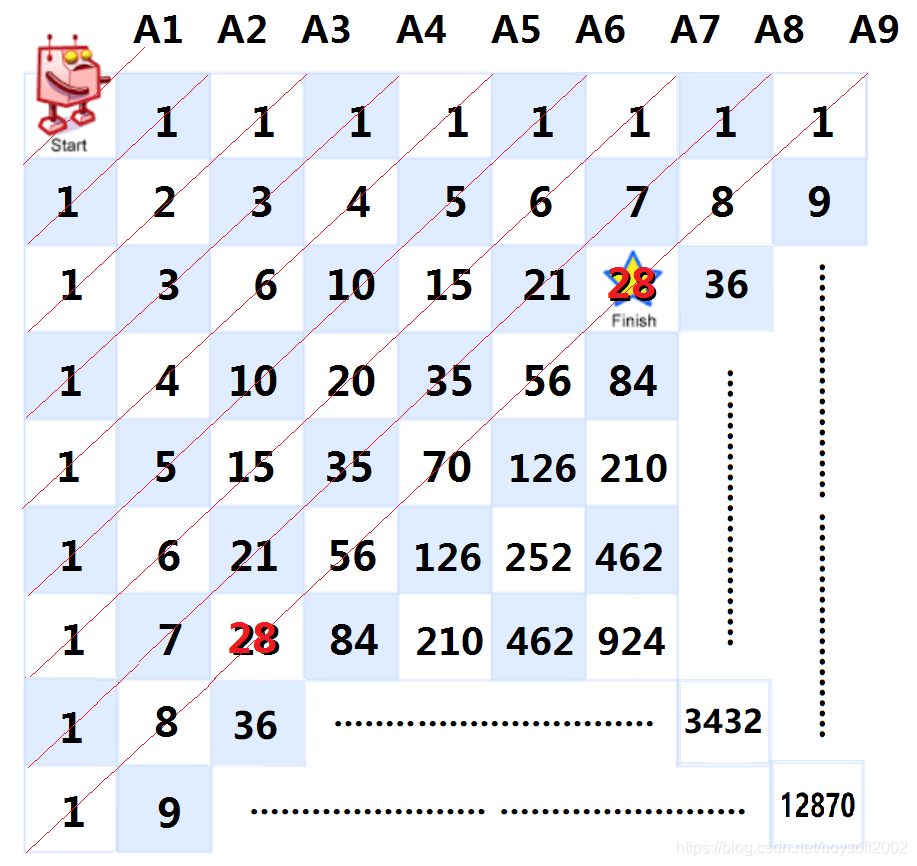
方法二：还是上面的思路，把地图扩展到正方形，如下图所示每条对角线串连的数字正好组成一个标准的杨辉三角形。如果杨辉三角形的每一行都用一个列表A表示，那么第m行第n列走法数值的所在位置就是列表 A[m+n-1] 的第m个数(或第n个，两者的值相等)。

代码如下：

>>> def YhPaths(m,n):
	i = m+n-1
	t = L = [1]
	while(i>1):
		i -= 1
		t = L+[t[n]+t[n+1] for n in range(len(t)-1)]+L
	return t[m-1]

>>> YhPaths(3,2)
3
>>> YhPaths(7,3)
28
>>> YhPaths(7,7)
924
>>> YhPaths(8,8)
3432
>>> YhPaths(9,9)
12870
>>>

杨辉三角形有很多种解法，稍作变形都可以成为本题的解法，所以方法二可以变化出一个系列的解法。比如，以下这个代码就比较精简：

>>> def YhPaths(m,n):
	L,n=[1],m+n-2
	for _ in range(n):L=[sum(_) for _ in zip([0]+L,L+[0])]
	return L[m-1]

方法三： 递归法，实用性不是不强，仅作一个递归实例学习。自己写了一个递归，当m、n的小者大于13时，因递归次数太多，用时有点过长了。递归法就是这个缺点：递归次数有限，耗时耗内存。看测试的规律在大于13阶后，阶数每增加1耗用的时间约为前一阶耗时的4倍左右。

>>> def recursion(m,n):
	if n>m: m,n=n,m  # 特别当m==n时如不交换多耗时50%，但交换错大小会更耗时
	if n<1: return 0
	if n==1:return 1
	if n==2:return m
	if n==3:return sum(range(m+1))
	if n==4:return sum([sum(range(i+1)) for i in range(m+1)])
	return sum([recursion(n-1,i) for i in range(m+1)])

>>> recursion(8,8)
3432
>>> recursion(9,9)
12870
>>> 
>>> # 时间测试
>>> from time import time
>>> t=time();recursion(14,14);time()-t
10400600
0.6708013248443604
>>> t=time();recursion(15,15);time()-t
40116600
2.4808049488067627
>>> t=time();recursion(16,16);time()-t
155117520
9.5400018148422241
>>> t=time();recursion(17,17);time()-t
601080390
36.812686896324158
>>> t=time();recursion(18,18);time()-t
2333606220
140.20606572151184
>>>

以下这个代码递归的更彻底，但耗时更厉害。递归法的本质是从终点把未知的答案用表达式往前递推；而前面的方法一、方法二是从起点用已知的结果向后递推；虽然方法不同，但实质用的表达式都是某一格的值等于前一格的值加上一格的值。

>>> def Recursion(m,n):
	if m==1 or n==1: return 1
	return Recursion(m,n-1)+Recursion(m-1,n)

>>> Recursion(3,7)
28
>>> Recursion(7,3)
28
>>> Recursion(9,9)
12870
>>> 
>>> from time import time
>>> t=time();Recursion(14,14);time()-t
10400600
2.5571463108062744
>>> t=time();Recursion(15,15);time()-t
40116600
9.740557193756104
>>> t=time();Recursion(16,16);time()-t
155117520
37.39713907241821
>>> t=time();Recursion(17,17);time()-t
601080390
145.44031858444214
>>>

方法四： 优化递归法。递归法的速度慢，是因为未知的值重复计算太多；稍加改进，把递归过程中已算过的中间结果存入一个全局变量中，这样已算过的就不再重复计算而是直接调用，可以大幅度提高效率。如下，设置一个列表data，作存储中间结果的全局变量，注意计算前一定要先设置好data的初值：

>>> init = lambda m,n:[[0]*(max(m,n)+1) for _ in range(max(m,n)+1)]
>>> def Recursion(m,n):
	global data
	if m==1 or n==1: return 1
	elif not data[m][n]:
		data[m][n]=Recursion(m-1,n)+Recursion(n-1,m)
	return data[m][n]

>>> m,n=3,7
>>> data=init(m,n);Recursion(m,n)
28
>>> m,n=7,3
>>> data=init(m,n);Recursion(m,n)
28
>>> m,n=9,9
>>> data=init(m,n);Recursion(m,n)
12870
>>> from time import time
>>> m,n=500,500
>>> t=time();data=init(m,n);Recursion(m,n);time()-t
676396999362954378167203938002941129870250271387758475994476664430994566
330135620366898107919175100513920435648202067329334859234361060854729465
014263059247806970681340720053443850010209554272633544980383181925937364
977441832552253540042528076643524441731372880722879385596666940182447106
60615920000
0.4687480926513672
>>> # 经过我的电脑测试，当m,n都大于513时就会超出最大递归深度而报错

方法五： 排列法。问题的本质：对m行n列的网格来说，就是n-1个Right和m-1个Down放到一起的排列问题，结果 result = (m-1+n-1)! / [(m-1)! * (n-1)!]。 排列公式也有很多种解法可用：

>>> def perm(n):
	s=1
	while n:
		s*=n
		n-=1
	return s

>>> def result(m,n):
	return perm(m+n-2)//perm(m-1)//perm(n-1)

>>> m,n = 3,2
>>> result(m,n)
3
>>> m,n = 7,3
>>> result(m,n)
28
>>> m,n = 3,7
>>> result(m,n)
28
>>>

方法六：组合法，来自于和杨辉三角有关联的二次项定理，其展开项通式： $T_{r+1} = C_{n}^{r} a^{n-r} b^{r}$ 。对于本题只需要它的系数部分，代入参数后实际的下标为m+n-2，上标为m-1或n-1；其实和方法四一样的，用公式计算的优点就是运行速度超快：

>>> def paths(m,n):
	ret = 1
	if n>m: m,n=n,m
	for i in range(1,n): ret=ret*(m+n-1-i)//i
	return ret

>>> paths(3,7)
28
>>> paths(7,3)
28
>>> paths(9,9)
12870
>>> 
>>> paths(1000,1000)
512294053774259558362972111801106814506359401696197357133662490663268680890966422168
317407249277190145438911035517264555381561230116189292650837306095363076178842645481
320822198226994485371813976409676367032381831285411152247284028125396742405627998638
503788368259307920236258027800099771751391617605088924033394630230806037178021722568
614945945597158227817488131642780881551702876651234929533423690387735417418121162690
198676382656195692212519230804188796272372873746380773141117366928488415626459630446
598074332450038402866155063023175006229242447751399777865500335793470023989772130248
615305440000
>>>

方法七：写成类class的形式，使用时有多种调用方法。注意直接使用 Yh(m,n)，它返回的值并不是一个整数，需要用int()强制转换；可以使用示例中的其他调用方法直接取得整数结果。

>>> class Yh():
	def __init__(self,m=1,n=1):
		self.data = 1
		if m!=1: self.data=Yh().N(m,n)
	def __repr__(self):
		return f'{self.data}'
	__str__ = __repr__
	def __int__(self):
		return self.value
	def N(self,m,n):
		self.data = [1]
		n=m+n-1
		while n>1:
			n-=1
			self.data.append(0)
			self.data=[sum(z) for z in zip(self.data,self.data[::-1])]
		return self.data[m-1]
	@property
	def value(self):
		return self.data

	
>>> Yh(3,7)
28
>>> Yh(7,3)
28
>>> Yh(9,9)
12870
>>> type(Yh(9,9))
<class '__main__.Yh'>
>>>
>>> int(Yh(7,7))
924
>>> int(Yh(8,8))
3432
>>> int(Yh(9,9))
12870
>>> 
>>> Yh(3,7).value
28
>>> Yh(9,9).value
12870
>>> type(Yh(9,9).value)
<class 'int'>
>>> 
>>> y = Yh()
>>> y.N(9,9)
12870
>>> y.N(3,7)
28
>>> type(y.N(7,3))
<class 'int'>
>>> 
>>> Yh().N(7,3)
28
>>> Yh().N(9,9)
12870
>>>

小结：上述几种方法中，用组合公式计算是最快的！

加强版第63题

当地图上的某一点出现障碍物，路径数有什么变化？？

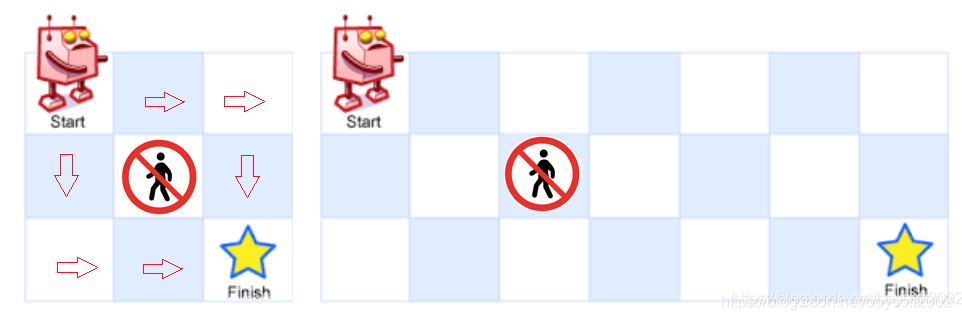
方法一：参照前一题方法一的思路，只是到有障碍的地方需要把走法数置为零。先来创建一个地图生成器：地图用来表示m行n列的网格，障碍位置x行y列，有障碍的位置为0，其余都为1（0和1的设置与原题目中的示例相反），如下：

>>> Map = lambda m,n,x,y:[[int((i,j)!=(x-1,y-1)) for j in range(n)] for i in range(m)]
>>> Map(3,3,2,2)
[[1, 1, 1], [1, 0, 1], [1, 1, 1]]
>>> Map(3,7,2,3)
[[1, 1, 1, 1, 1, 1, 1], [1, 1, 0, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1]]
>>>

然后在此地图的第二行第二列开始照前一题的样子“做加法”，但遇到0要跳过：

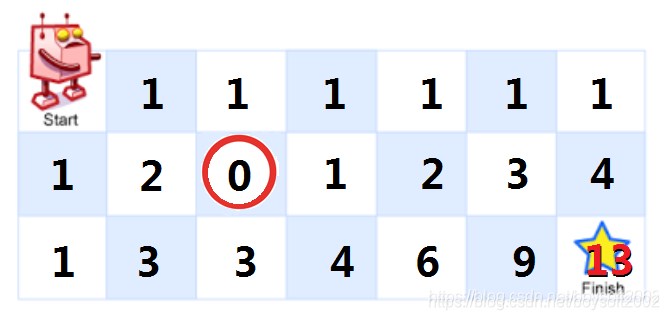
特例：当障碍出现在首行(或首列)时，障碍右边(或正下方)的格子都是机器人到不了的地方，所以障碍及其右侧(或下方)的格子都要置数为0，如下图所示：

代码如下：

>>> def Paths(m=3,n=3,x=2,y=2):
    '''有障碍走法，网格mxn障碍坐标(x,y)'''
	map = [[int((i,j)!=(x-1,y-1)) for j in range(n)] for i in range(m)]
	if x==1:map[0][y-1:]=[0]*(len(map[0])-y+1)
	if y==1:
		for i in range(x-1,len(map)):
			map[i][0]=0
	for i in range(1,m):
		for j in range(1,n):
			if map[i][j]!=0:
				map[i][j]=map[i-1][j]+map[i][j-1]
	return map[m-1][n-1]

>>> def paths(m,n):
    '''无障碍走法，网格mxn'''
	r = [[1 for _ in range(m)] for _ in range(n)]
	for i in range(1,n):
		for j in range(1,m):
			r[i][j] = r[i-1][j]+r[i][j-1]
	return r[n-1][m-1]
 
>>> Paths()
2
>>> Paths(3,7,2,3)
13
>>>
>>> # 障碍出现在首列
>>> Paths(4,7,2,1)
56
>>> paths(4,6)
56
>>> Paths(4,7,3,1)
77
>>> paths(3,6)
21
>>> paths(4,6)+paths(3,6)
77
>>> # 障碍出现在首行
>>> Paths(4,7,1,4)
64
>>> paths(3,7)
28
>>> paths(3,6)
21
>>> paths(3,5)
15
>>> paths(3,7)+paths(3,6)+paths(3,5)
64
>>> # 障碍出现在起点或终点，走法数都为0
>>> Paths(4,7,1,1)
0
>>> Paths(4,7,4,7)
0
>>>

方法二：解题思路是用无障碍时的走法总数减去经过障碍那一点的走法数；后者等于起点到障碍点的走法数与障碍点到终点的走法数的乘积。调用上一题的paths(m,n)，引入障碍坐标x,y表示x行y列有障碍。所求结果即等于： paths(m,n) - paths(x,y)*paths(m-x+1,n-y+1)

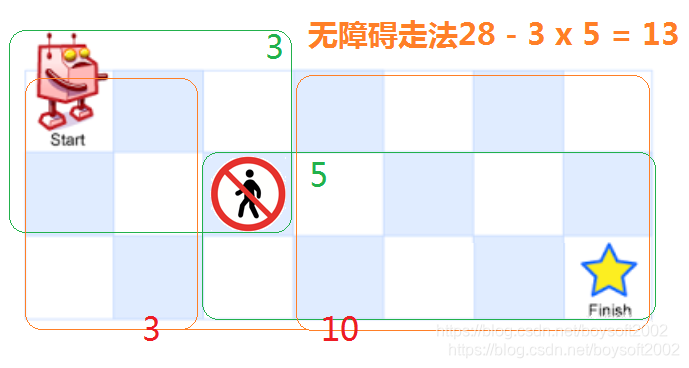
代码如下：

>>> def paths(m,n):
	r = [[1]*m for _ in range(n)]
	for i in range(1,n):
		for j in range(1,m):
			r[i][j] = r[i-1][j]+r[i][j-1]
	return r[n-1][m-1]

>>> def Paths(m,n,x,y):
	return paths(m,n) - paths(x,y)*paths(m-x+1,n-y+1)

>>> m,n=3,3; x,y=2,2
>>> Paths(m,n,x,y)
2
>>> m,n=3,7; x,y=2,3
>>> Paths(m,n,x,y)
13
>>>

当问题扩展到有多个障碍物时，凡是有障碍的格子就都置成0估计也能成立(没实测)！

————===== The End =====————