激活函数的作用

内容来自：
https://www.zhihu.com/question/22334626
http://blog.youkuaiyun.com/cyh_24/article/details/50593400

首先摆结论，因为线性模型的表达能力不够，引入激活函数是为了添加非线性因素。
接下来展开来说。

为什么要引入激活函数？

在神经网络中，每一层输出的都是上一层输入的线性函数，所以无论网络结构怎么搭，输出都是输入的线性组合。

单层的感知机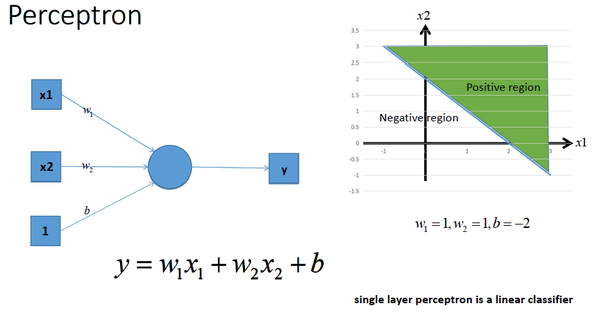

图片被知乎挂掉啦，可以去原文查看~

用多个感知机来进行组合, 获得更强的分类能力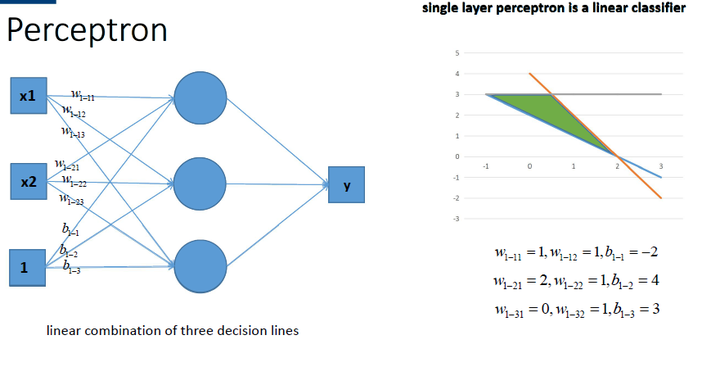

组合输出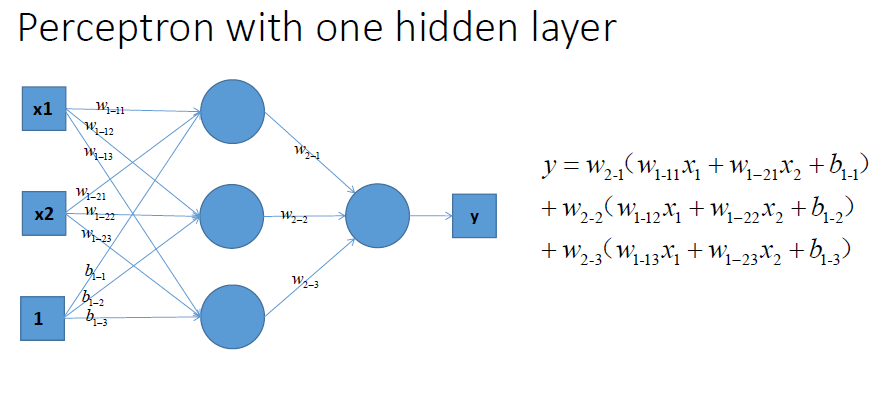

所以从上图可以看出，不论怎么组合，都是输出都是输入的线性变换，无法做到非线性分类。

下图采用step activation function（阶跃激活函数）获得的分类器，其实只能还是线性的, 最多不过是复杂的线性组合罢了~~~当然你可以说我们可以用无限条直线去逼近一条曲线啊......额,当然可以, 不过比起用non-linear的activation function来说就太傻了嘛....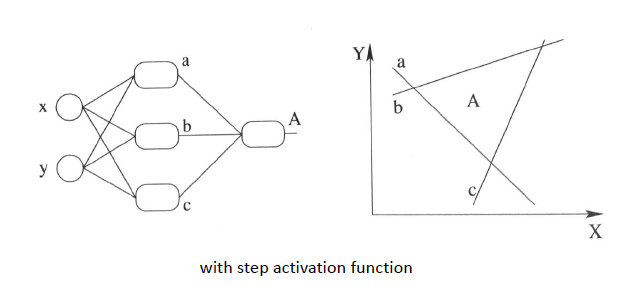

激活函数的作用？

引入非线性因素。

在我们面对线性可分的数据集的时候，简单的用线性分类器即可解决分类问题。但是现实生活中的数据往往不是线性可分的，面对这样的数据，一般有两个方法：引入非线性函数、线性变换。

线性变换

就是把当前特征空间通过一定的线性映射转换到另一个空间，让数据能够更好的被分类。

激活函数

激活函数是如何引入非线性因素的呢？在神经网络中，为了避免单纯的线性组合，我们在每一层的输出后面都添加一个激活函数（sigmoid、tanh、ReLu等等），这样的函数长这样：

Sigmoid & Tanh

ReLU

每一层的输出通过这些激活函数之后，就变得比以前复杂很多，从而提升了神经网络模型的表达能力。当然怎么选择这个激活函数，还是很需要一些trick的。

如果你使用 ReLU，那么一定要小心设置 learning rate，而且要注意不要让你的网络出现很多 “dead”
神经元，如果这个问题不好解决，那么可以试试 Leaky ReLU、PReLU 或者 Maxout.

友情提醒：最好不要用 sigmoid，你可以试试 tanh，不过可以预期它的效果会比不上 ReLU 和 Maxout.

还有，通常来说，很少会把各种激活函数串起来在一个网络中使用的。

一些常见的激活函数

Sigmoid

（左sigmoid右tanh）

Sigmoid 是常用的非线性的激活函数，它的数学形式如下：

$$f(x)=\frac{1}{1+e^{−x}}$$
它能够把输入的连续实值“压缩”到0和1之间。
特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1.
sigmoid 函数曾经被使用的很多，不过近年来，用它的人越来越少了。主要是因为它的一些 缺点：

• Sigmoids saturate and kill gradients. 这就是我们常常提到的梯度消失问题啦。sigmoid 有一个非常致命的缺点，当输入非常大或者非常小的时候（saturation），这些神经元的梯度是接近于0的，从图中可以看出梯度的趋势。所以，你需要尤其注意参数的初始值来尽量避免saturation的情况。如果你的初始值很大的话，大部分神经元可能都会处在saturation的状态而把gradient kill掉，这会导致网络变的很难学习。
• Sigmoid 的 output 不是0均值. 这是不可取的，因为这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。 产生的一个结果就是：如果数据进入神经元的时候是正的($e.g. x>0\space \ \ elementwise \ \ in\ \ f=w^Tx+b$)，那么 w 计算出的梯度也会始终都是正的。
  当然了，如果你是按batch去训练，那么那个batch可能得到不同的信号，所以这个问题还是可以缓解一下的。因此，非0均值这个问题虽然会产生一些不好的影响，不过跟上面提到的 kill gradients 问题相比还是要好很多的。

tanh

tanh 是sigmoid的变形：

$$tanh(x)=2sigmoid(2x)−1$$
与 sigmoid 不同的是，tanh 是0均值的。因此，实际应用中，tanh 会比 sigmoid 更好（毕竟去粗取精了嘛）。

ReLU

近年来，ReLU 变的越来越受欢迎。它的数学表达式如下：

$$f(x)=max(0,x)$$
很显然，从图左可以看出，输入信号<0时，输出都是0，>0 的情况下，输出等于输入。w 是二维的情况下，使用ReLU之后的效果如下：

优点：
Krizhevsky et al. 发现使用 ReLU 得到的SGD的收敛速度会比 sigmoid/tanh 快很多(看右图)。有人说这是因为它是linear，而且 non-saturating
相比于 sigmoid/tanh，ReLU 只需要一个阈值就可以得到激活值，而不用去算一大堆复杂的运算。
缺点：
当然 ReLU 也有缺点，就是训练的时候很”脆弱”，很容易就”die”了. 什么意思呢？

举个例子：一个非常大的梯度流过一个 ReLU 神经元，更新过参数之后，这个神经元再也不会对任何数据有激活现象了。
如果这个情况发生了，那么这个神经元的梯度就永远都会是0.

实际操作中，如果你的learning rate 很大，那么很有可能你网络中的40%的神经元都”dead”了。
当然，如果你设置了一个合适的较小的learning rate，这个问题发生的情况其实也不会太频繁。

Leaky ReLUs

就是用来解决这个 “dying ReLU” 的问题的。与 ReLU 不同的是：

$$f(x)=αx，(x<0)$$

$$f(x)=x，(x>=0)$$
这里的 $α$ 是一个很小的常数。这样，即修正了数据分布，又保留了一些负轴的值，使得负轴信息不会全部丢失。

关于Leaky ReLU 的效果，众说纷纭，没有清晰的定论。有些人做了实验发现 Leaky ReLU 表现的很好；有些实验则证明并不是这样。

Parametric ReLU

对于 Leaky ReLU 中的α，通常都是通过先验知识人工赋值的。
然而可以观察到，损失函数对α的导数我们是可以求得的，可不可以将它作为一个参数进行训练呢？
Kaiming He的论文《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》指出，不仅可以训练，而且效果更好。

公式非常简单，反向传播至未激活前的神经元的公式就不写了，很容易就能得到。对α的导数如下：

$$\frac{δy_i}{δα}=0，(if\ y_i>0)，else=y_i$$
原文说使用了Parametric ReLU后，最终效果比不用提高了1.03%.

Randomized ReLU：

Randomized Leaky ReLU 是 leaky ReLU 的random 版本 （α 是random的）.
它首次试在 kaggle 的NDSB 比赛中被提出的。

核心思想就是，在训练过程中，α 是从一个高斯分布 U(l,u) 中 随机出来的，然后再测试过程中进行修正（有点像dropout的用法）。
数学表示如下:

在测试阶段，把训练过程中所有的 $α_{ij}$ 取个平均值。NDSB 冠军的 $α$ 是从 $U(3,8)$ 中随机出来的。那么，在测试阶段，激活函数就是就是：

$$y_{ij} = \frac{x_{ij}}{\frac{l+u}{2}}$$

Maxout

Maxout出现在ICML2013上，作者Goodfellow将maxout和dropout结合后，号称在MNIST, CIFAR-10, CIFAR-100, SVHN这4个数据上都取得了start-of-art的识别率。
Maxout 公式如下：

$$f_i(x)=max_{j\in [1,k]}z_{ij}$$
假设 w 是2维，那么有：
$$f(x)=max(w_1^Tx+b_1,w_2^Tx+b_2)$$
可以注意到，ReLU 和 Leaky ReLU 都是它的一个变形（比如，w1,b1=0 的时候，就是 ReLU）.

Maxout的拟合能力是非常强的，它可以拟合任意的的凸函数。作者从数学的角度上也证明了这个结论，即只需2个maxout节点就可以拟合任意的凸函数了（相减），前提是”隐隐含层”节点的个数可以任意多.

所以，Maxout 具有 ReLU 的优点（如：计算简单，不会 saturation），同时又没有 ReLU 的一些缺点 （如：容易 go die）。不过呢，还是有一些缺点的嘛：就是把参数double了。

其他激活函数