poj 1170 shopping offers

 

Shopping Offers

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 2286		Accepted: 866

Description

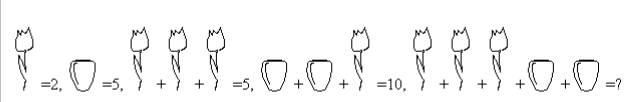
In a shop each kind of product has a price. For example, the price of a flower is 2 ICU (Informatics Currency Units) and the price of a vase is 5 ICU. In order to attract more customers, the shop introduces some special offers. 
A special offer consists of one or more product items for a reduced price. Examples: three flowers for 5 ICU instead of 6, or two vases together with one flower for 10 ICU instead of 12. 
Write a program that calculates the price a customer has to pay for certain items, making optimal use of the special offers. That is, the price should be as low as possible. You are not allowed to add items, even if that would lower the price. 
For the prices and offers given above, the (lowest) price for three flowers and two vases is 14 ICU: two vases and one flower for the reduced price of 10 ICU and two flowers for the regular price of 4 ICU. 

Input

Your program is to read from standard input. The first line contains the number b of different kinds of products in the basket (0 <= b <= 5). Each of the next b lines contains three values c, k, and p. The value c is the (unique) product code (1 <= c <= 999). The value k indicates how many items of this product are in the basket (1 <= k <= 5). The value p is the regular price per item (1 <= p <= 999). Notice that all together at most 5*5=25 items can be in the basket. The b+2nd line contains the number s of special offers (0 <= s <= 99). Each of the next s lines describes one offer by giving its structure and its reduced price. The first number n on such a line is the number of different kinds of products that are part of the offer (1 <= n <= 5). The next n pairs of numbers (c,k) indicate that k items (1 <= k <= 5) with product code c (1 <= c <= 999) are involved in the offer. The last number p on the line stands for the reduced price (1 <= p <= 9999). The reduced price of an offer is less than the sum of the regular prices.

Output

Your program is to write to standard output. Output one line with the lowest possible price to be paid.

Sample Input

2
7 3 2
8 2 5
2
1 7 3 5
2 7 1 8 2 10

Sample Output

14

Source

IOI 1995

 

/*

http://acm.pku.edu.cn/JudgeOnline/problem?id=1170
 状态压缩DP
 最多有5类产品,每类最多有5个,则可以将没个产品的数量用一个6进制位来表示,这样5类产品最多需要
 5个六进制位来表示整个状态,一个有6 ^ 5 - 1 = 7775 个状态,所有用一个大小是7775的数组来记录
 当前状态的最优价格

*/

#include <iostream> #include <cmath> #define MAX_S 7775 #define MAX_P 5 #define MAX_C 99 #define MAX_VAL 10000000 using namespace std; int minCost[MAX_S + 1]; //记录产品结构 struct product { int id; //id int num; //数量 int price; //价格 }products[MAX_P + 1]; int pNum; //产品的种类数 //记录组合方案的结构 struct combine { //记录各类产品所需的数量 int num[MAX_P + 1]; //优惠的总价格 int price; combine() { for(int i = 0; i <= MAX_P; i++) num[i] = 0; } }combines[MAX_C + 1]; //组合方案数以及当前总状态六进制的10进制形式 int cNum, state = 0; //返回id为id的商品的下标 int getIndex(int id) { for(int i = 0; i < pNum; i++) if(products[i].id == id) return i; return -1; //not found } //从当前状态中得到第index个商品的数量 void getNums(int curState, int nums[]) { for(int i = 0; i < pNum; i++) { nums[i] = curState % 6; curState /= 6; } } //从当前记录了各个产品数量的数组得到总状态六进制表示的10进制形式 int getState(int nums[]) { int state = 0; for(int i = 0; i < pNum; i++) state = state + nums[i] * pow(double(6), i); return state; } //当前各产品数量记录在nums中,此函数尝试使用组合方案combId //若可行则计算buyNum, remainNum数组并返回1,若不可行则返回0 int checkCombine(int nums[], int buyNum[], int remainNum[], int combId) { for(int i = 0; i < pNum; i++) { if(nums[i] >= combines[combId].num[i]) { buyNum[i] = combines[combId].num[i]; remainNum[i] = nums[i] - combines[combId].num[i]; } else return 0; } return 1; } int dpSolve(int curState) { //cout<<curState<<endl; if(minCost[curState] != MAX_VAL) return minCost[curState]; int nums[MAX_P + 1]; //从状态中得到各个product的数量 getNums(curState, nums); //存储购买的数量 int buyNum[MAX_P + 1], i; int remainNum[MAX_P + 1]; int minV = MAX_VAL, curV; //遍历组合方案 for(i = 0; i < cNum; i++) { if(checkCombine(nums, buyNum, remainNum, i)) { //尝试当前组合方案 curV = combines[i].price + dpSolve(getState(remainNum)); if(curV < minV) minV = curV; } } int res = 0; //若无组合优惠方案可用则只能全部按照正常模式逐一购买 if(minV == MAX_VAL) { for(i = 0; i < pNum; i++) res = res + products[i].price * nums[i]; } else res = minV; minCost[curState] = res; return res; } int main() { int i, j; cin>>pNum; for(i = 0; i < pNum; i++) { cin>>products[i].id>>products[i].num>>products[i].price; state = state + pow(double(6), i) * products[i].num; //转换成6进制进行状态压缩 } //初始化 for(i = 0; i <= state; i++) minCost[i] = MAX_VAL; minCost[0] = 0; cin>>cNum; int tempCNum, tempId, tempNum, tempIndex, tempType; for(i = 0; i < cNum; i++) { tempType = 0; cin>>tempCNum; for(j = 0; j < tempCNum; j++) { cin>>tempId>>tempNum; tempIndex = getIndex(tempId); //tempType = tempType + pow(double(6), j) * tempNum; combines[i].num[tempIndex] = tempNum; } cin>>combines[i].price; } dpSolve(state); cout<<minCost[state]<<endl; return 0; }