回归中的相关度和决定系数

最新推荐文章于 2024-11-08 13:43:29 发布

原创最新推荐文章于 2024-11-08 13:43:29 发布 · 3.4k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #Conv&R

机器学习同时被 2 个专栏收录

19 篇文章

订阅专栏

常见的机器学习方法

14 篇文章

订阅专栏

本文介绍了皮尔逊相关系数和决定系数的概念及其计算方法。皮尔逊相关系数用于衡量两个变量间的线性相关性，其值范围在-1到1之间。决定系数(R²)则反映了自变量能够解释因变量变异的比例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

训练集中可能是有若干维度的特征。但有时并不是所有特征都是有用的，有的特征其实和结果并没有关系。因此需要一个能衡量自变量和因变量之间的相关度。

皮尔逊相关系数

皮尔逊相关系数(Pearson correlation coefficient），是用于度量两个变量 X 和 Y 之间的相关（线性相关），其值介于[-1,1] 之间。有三种相关情况：

正向相关: >0
负向相关：<0
无相关性：=0

下图从左到右分别代表了正向相关、无相关性和负向相关：

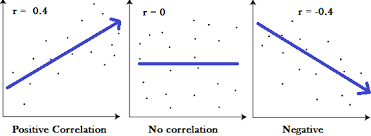
在介绍皮尔逊相关系数之前，要先理解协方差(Covariance ) ，协方差是一个反映两个随机变量相关程度的指标，如果一个变量跟随着另一个变量同时变大或者变小，那么这两个变量的协方差就是正值，反之相反，公式如下：
$\frac{\sum_{i=1}^{n}(X_i-\overline{X})(Y_i-\overline{Y})}{n-1}$
皮尔逊相关系数的公式如下：
$r_{xy} = \frac{Conv(X,Y)}{\sqrt{Var(X)Var(Y)}} = \frac{\sum(x-\overline{x})(y-\overline{y})}{\sqrt{\sum{(x-\overline{x})^2}\sum(y-\overline{y})^2}}$
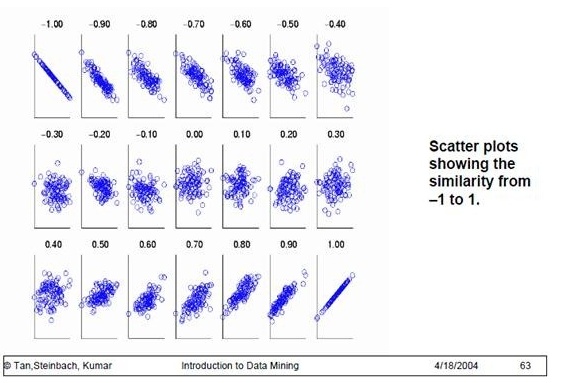
Var表示方差，相关度越高，皮尔逊相关系数其值趋于 1 或 -1 （趋于1表示它们呈正相关，趋于 -1 表示它们呈负相关）；如果相关系数等于0，表明它们之间不存在线性相关关系。

决定系数

决定系数即 R 平方值，反应因变量的全部变异能通过回归关系被自变量解释的比例。如R平方为0.8，则表示回归关系可以解释因变量80%的变异。换句话说，如果我们能控制自变量不变，则因变量的变异程度会减少 80%。在简单线性回归中，决定系数可以是 R^2 = r * r。而更通用的是：

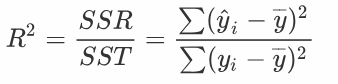
SST 其实是两部分组成的，一部分是模型可预测的SSR，一部分是变异的SSError无法用模型解释的。它们之间的计算公式是:

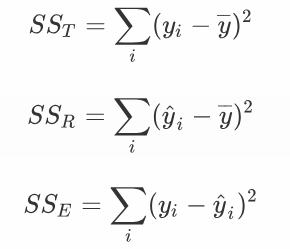
注意: R平方也有其局限性：R平方随着自变量的增加会变大，R平方和样本量是有关系的。因此，我们要到R平方进行修正。修正的方法：
$\overline{R^2} = 1-(1-R^2)\frac{n-1}{n-p-1}$
其中，n 表示样本大小，p 表示模型中解释变量的总数（不包括常数）。

代码实例

代码完全按照上述中的公式计算

import numpy as np
import math
from sklearn import linear_model

#计算皮尔逊相关系数( Pearson correlation coefficient）
def computer_conv(x,y):
    var_x = 0
    var_y = 0
    SSR = 0
    x_bar = np.mean(x) # x的方差
    y_bar = np.mean(y) # y的方差
    for i in range(len(x)):
        diff_xbar = x[i] - x_bar
        diff_ybar = y[i] - y_bar
        SSR += diff_xbar * diff_ybar
        var_x += diff_xbar**2
        var_y += diff_ybar**2
    SST = math.sqrt(var_x*var_y)
    return SSR/SST

#计算决定系数R平方值
def computer_r(x,y):
    SSR = 0
    SST = 0
    linear = linear_model.LinearRegression() # 创建线性模型
    linear.fit(x,y)
    y_hat = linear.predict(x)
    y_mean = np.mean(y)
    for i in range(len(x)):
        SSR += (y_hat[i] - y_mean)**2
        SST += (y[i] - y_mean)**2
    return SSR/SST

test_x = [1,3,8,7,9]
test_y = [10,12,24,21,34]
test_x2 = [[x] for x in test_x]

print("r: ",computer_conv(test_x,test_y))
print("r平方: ",computer_conv(test_x,test_y)**2)
print("R平方: ",computer_r(test_x2,test_y))

程序运行结果

r:  0.94031007654487
r平方:  0.8841830400518192
R平方:  0.8841830400518192

**我们发现：**在简单线性回归中，决定系数的确满足$ R^2 = r * r$