吴恩达机器学习笔记之支持向量机

本文链接：https://blog.youkuaiyun.com/blue_coffeei/article/details/87874255

本文深入探讨支持向量机（SVM）的优化目标、大间距分类的直观理解及其数学原理。SVM通过最大化间隔实现有效分类，而核函数则允许处理非线性问题。介绍了高斯核函数的工作原理及其在不同场景下的应用，并提供了选择逻辑回归还是SVM的指南。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

优化目标（Optimization Objective）：

Support Vector Machines（SVMs）支持向量机是一种非常强大的算法，在学习复杂的非线性方程时提供了一种更为清晰，更加强大的方式。我们首先从优化目标开始一步一步认识SVMs，首先从逻辑回归的优化目标开始：

下图是逻辑回归中的假设函数-sigmoid函数，

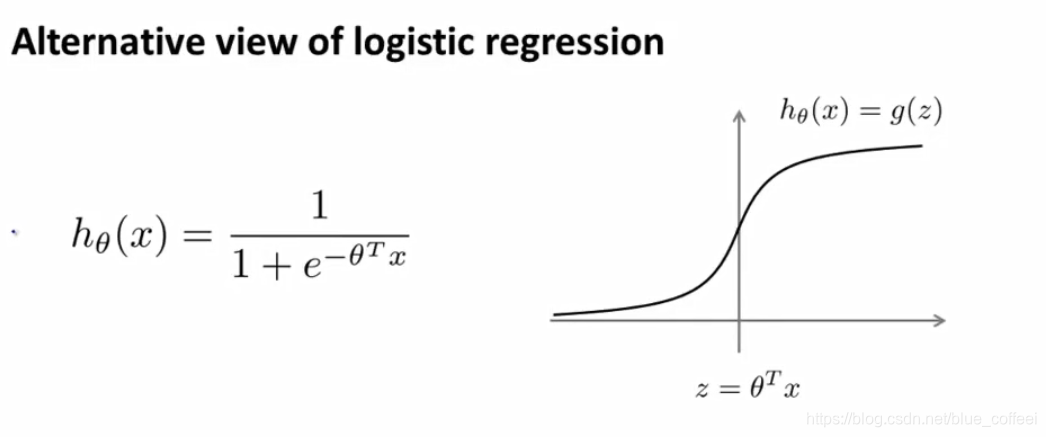
我们已经清楚的知道逻辑回归的优化目标，下图表示的为一个样本对于总体优化目标的贡献：

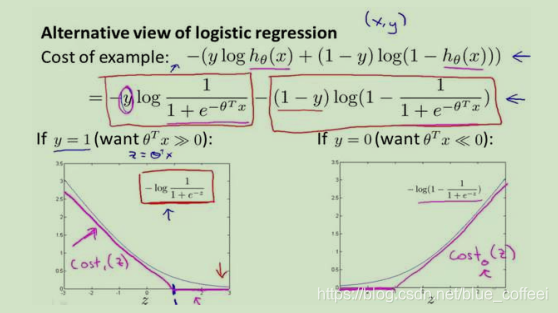
图中紫红色的线表示的SVMs的优化目标中对逻辑回归的一点修改，我们通过去除m，并且通过系数调整，让正则化项中的lambda变成1，在前面的代价函数中增加系数C，这样的目的只是为了换一种形式表达，其物理意义还是通过C的值来改变代价函数或者正则项在优化目标中的权重。得到的SVMs的优化目标如下所示：

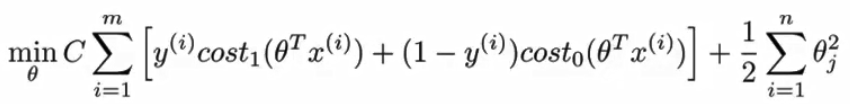
另外，值得注意的是SVMs输出的结果不像逻辑回归一样是概率，而是直接输出是0或者是1，学习参数theta就是SVMs的假设函数形式。

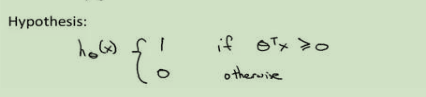
直观上对大间隔的理解（Large Margin Intuition）：

SVMs也被叫做大间距分类器，意思是SVMs会以最大的间隔来分离正负样本，如下图所示，绿色和粉红色的线虽然可以将样本分开，但是如果用大间距分类，得到的结果是中间那条黑色的线，可以看到与黑色的线平行的两条绿色的线，虽然也可以分离样本，但是不符合最大间距的思想。这也是为什么当C设置非常大的时候，把它叫做大间距分类器的原因。

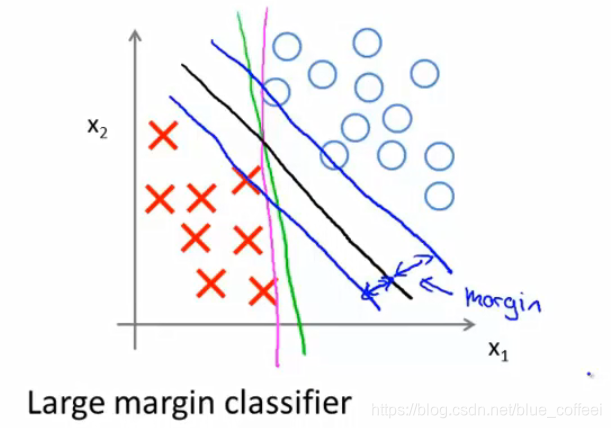
但是如果分类之后出现了一个异常的数据，比如下图左下角的红叉，那么如果我们还将C设置的非常大的话，即还是使用大间距分类的话，那么我们的决策边界就会由黑色的线变成粉红色的线，但是这不是一个好主意。那么有趣的是，SVMs做的其实远不止大间距分类，这个时候如果我们不在把C设置的很大，而是一个相对来说足够小的数，那么我们SVMs得到的决策边界就仍然是黑色的那条线。对于非线性可分的数据集，我们的SVMs也能将数据集进行很好的划分。

这只是为了让我们对大间距分类有一个更直观的印象和了解，这里的参数C我们可以将它的作用想象成1/lambda，当C很大时，对应的是lambda很小，C很小时，对应的是lambda很大。