C++中关于树的一些定义

概念

本文以一个简单的树为例，如下图，来记录树的一些概念。

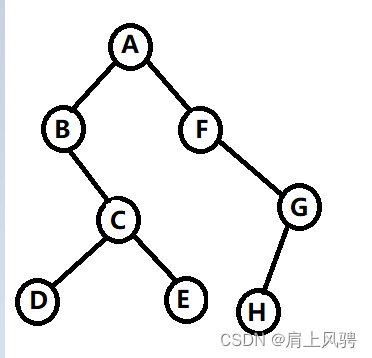
树

一种由n个节点组成的具有一定层次关系的有限数据集合。每个节点有0个或者n个子节点，有一个根节点（没有前驱只有后继），除根节点外每一个节点都有一个前驱，0个或多个后继。

树的叶子节点

只有一个前驱，没有后继的节点，为最外层的节点。叶子节点的度为0。

节点的度

节点拥有的子树的数目。

分支结点

度不为0的结点。

树的度

树中结点的最大的度。

树的高度

任意叶子节点距离根节点的最大深度。此文中树的叶子节点为D、E、H，距离根节点的深度都为4，故高度为4。

树的深度

即从根节点到叶子节点的行数。此文中树的深度为4。

注意

树的层次，深度和高度值得是同一个值，可记为行数。树的度为树中所有节点中节点的度最大的值。

二叉树

二叉树是每个节点最多有两个子树的树结构。
它有五种基本形态：
二叉树可以是空集；
根可以有空的左子树或右子树；
或者左、右子树皆为空。

二叉树的特点

二叉树第i层上的结点数目最多为2^(i-1）(i>=1)
深度为k的二叉树至多有2^k-1个结点（k>=1）
包含n个结点的二叉树的高度至少为(log2n)+1

满二叉树

高度为h，并且由2^h-1个节点组成的二叉树。

完全二叉树

• 若设二叉树的深度为h，除第h层外，其它各层（1~h-1）的结点数都达到最大个数，第h层所有的结点都连续集中在最左边。
• 对一颗具有n个结点的二叉树按层编号，如果编号为i（1≤i≤n）的结点与同样深度的满二叉树中编号为i的结点在二叉树中的位置完全相同，则这棵二叉树称为完全二叉树。

完全二叉树的特点包括：

• 叶子结点只能出现在最下层和次下层。
• 最下层的叶子结点集中在树的左部。
• 倒数第二层若存在叶子结点，一定在右部连续位置。
• 如果结点度为1，则该结点只有左孩子，即没有右子树。
• 同样结点数目的二叉树，完全二叉树深度最小。
  此外，满二叉树一定是完全二叉树，但反过来不一定成立。对于深度为K的、有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时，称之为完全二叉树。

二叉查找树

二叉查找树又被称为二叉搜索树。设x为二叉查找树中的一个结点，x结点包含关键字key，结点x的key值计为key[x]。如果y是x的左子树中的一个结点，则key[y]<=key[x]；如果y是x的右子树的一个结点，则key[y]>=key[x]。
特点：
1.若任意结点的左子树不空，则左子树上所有结点的值均小于它的根结点的值。
2.任意结点的右子树不空，则右子树上所有结点的值均大于它的根结点的值。
3.任意结点的左、右子树也分别为二叉查找树。
4.没有键值相等的结点。

示例

下面直接上代码，一个简单的树的创建、遍历输出，叶子节点数，高度。

代码实现

Tree.h

#pragma once

typedef struct MYTREE {
	char data;
	struct MYTREE* lChild;
	struct MYTREE* rChild;
}MyTree;

class Tree
{
public:
	Tree();
	~Tree();

	void CreateTree();
	void TraverseTree(MyTree *root);
	void GetLeafNode(MyTree *root,int &num);
	int GetTreeDepth(MyTree *root);
	void GetTreeNode(MyTree *root, int &num);
};

Tree.cpp

#include "Tree.h"
#include <iostream>
#include<algorithm>//max,min
using namespace std;

Tree::Tree()
{

}

Tree::~Tree()
{

}

void Tree::CreateTree()
{
	MyTree t1 = {'A',nullptr,nullptr};
	MyTree t2 = { 'B',nullptr,nullptr };
	MyTree t3 = { 'C',nullptr,nullptr };
	MyTree t4 = { 'D',nullptr,nullptr };
	MyTree t5 = { 'E',nullptr,nullptr };
	MyTree t6 = { 'F',nullptr,nullptr };
	MyTree t7 = { 'G',nullptr,nullptr };
	MyTree t8 = { 'H',nullptr,nullptr };

	t1.lChild = &t2;
	t1.rChild = &t6;
	t2.rChild = &t3;
	t3.lChild = &t4;
	t3.rChild = &t5;
	t6.rChild = &t7;
	t7.lChild = &t8;

	TraverseTree(&t1);
	cout << endl;
	int leafNum = 0;
	GetLeafNode(&t1,leafNum);
	cout << "leaf num: " << leafNum << endl;
	int treeDepth = GetTreeDepth(&t1);
	cout << "depth:" << treeDepth << endl;
	int nodeNum = 0;
	GetTreeNode(&t1,nodeNum);
	cout << "node num; " << nodeNum << endl;
}

void Tree::TraverseTree(MyTree *root)
{
	if (root == nullptr)
	{
		return;
	}
	

	TraverseTree(root->lChild);
	cout << root->data;
	TraverseTree(root->rChild);

}

void Tree::GetLeafNode(MyTree *root,int &num)
{
	if (root == nullptr)
	{
		return ;
	}
	if (root->lChild == nullptr && root->rChild == nullptr)
	{
		num++;
	}

	GetLeafNode(root->lChild,num);
	GetLeafNode(root->rChild,num);
}

int Tree::GetTreeDepth(MyTree * root)
{
	int num = 0;
	if (root == nullptr)
	{
		return num;
	}

	int lNum = GetTreeDepth(root->lChild);
	int rNum = GetTreeDepth(root->rChild);

	return max(lNum,rNum)+1;
}

void Tree::GetTreeNode(MyTree * root, int & num)
{
	if (root == nullptr)
	{
		return;
	}
	++num;
	GetTreeNode(root->lChild,num);
	GetTreeNode(root->rChild,num);
}

main.cpp

#include <iostream>
#include "Tree.h"
using namespace std;

void test() {
	Tree t;
	t.CreateTree();
}

int main()
{
	test();

	return 0;
}

开发环境

vs2017控制台输出程序。

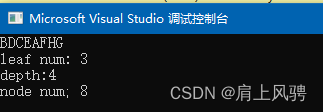
运行结果