【矩阵论笔记】诱导范数

从矩阵范数的定义中，多了一个相容性。因为抽象空间中的向量是不能乘的，但是矩阵是可以乘的。直接定义满足这四个条件的范数很难，直接定义非常麻烦。
为了定义相容的矩阵范数，引出一个方法：诱导范数。

诱导范数的定义

给矩阵A乘一个单位向量，相当于对单位向量做了一次变换，假设变换是下面图中所示的。$||Ax||$就有一个长度，就是一个范数。我们把矩阵$A$的范数称为$||A||$.

定理

证明

证两个方向

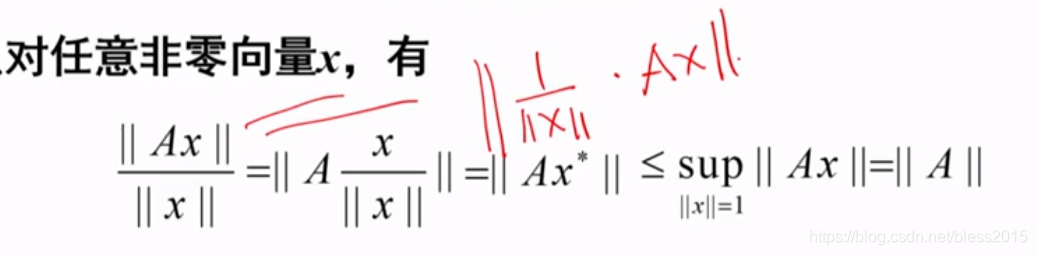
诱导范数和向量范数的相容性

常用诱导范数

如果按定义去计算$||Ax||$的范数会很麻烦，首先要计算$Ax$，最后是一个向量，然后如果计算1范数的话，就在把每一列绝对值加和。
有种简单的计算方式：

上面的公式解决了由向量1范数、2范数、无穷范数诱导出来的矩阵范数的计算。
对一式进行证明：

$x$是一个单位向量。注意诱导范数都是由单位向量诱导出来的。由于向量$x$的1范数满足三角不等式，也就是$A_1{x}_1+A_2{x}_2+A_3{x}_3...$满足三角不等式，所以可以写成下面的形式。
先证小于等于：

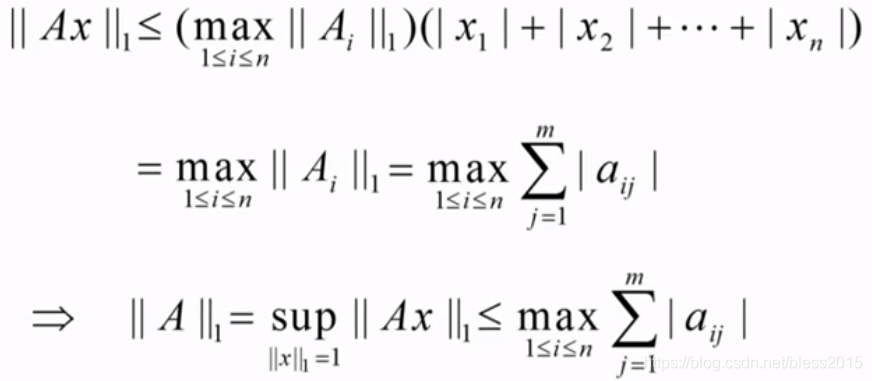
取了个特殊的向量证大于等于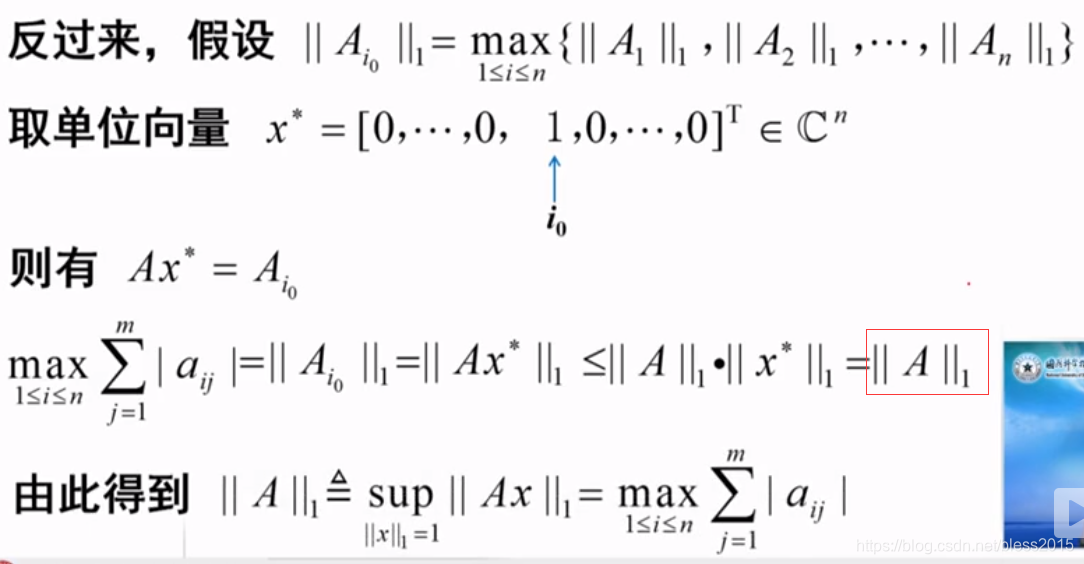
从而只能相等。

范数例题

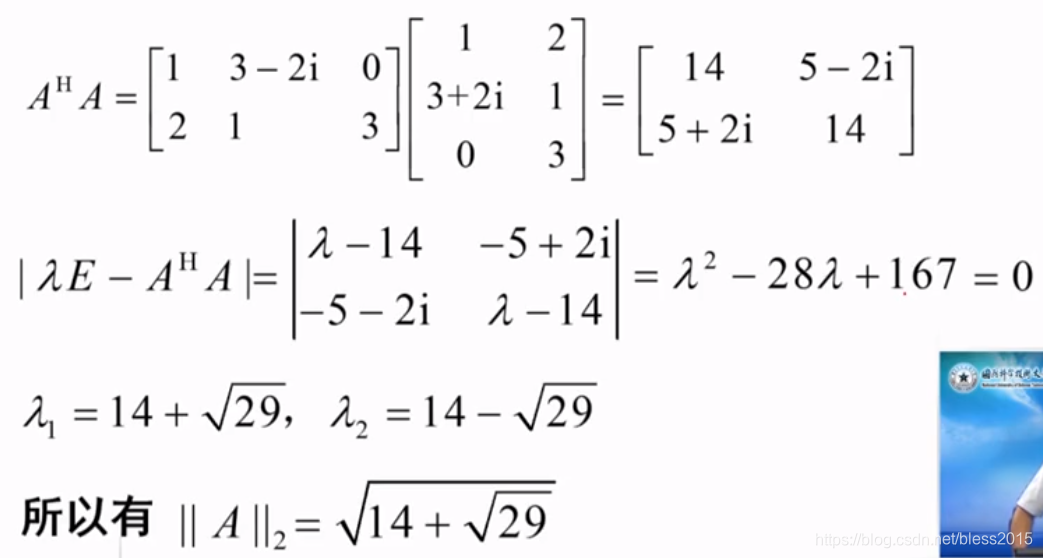
注意是共轭转置，有复数的话，要变符号。