图像增强

图像增强方法分为两大类：

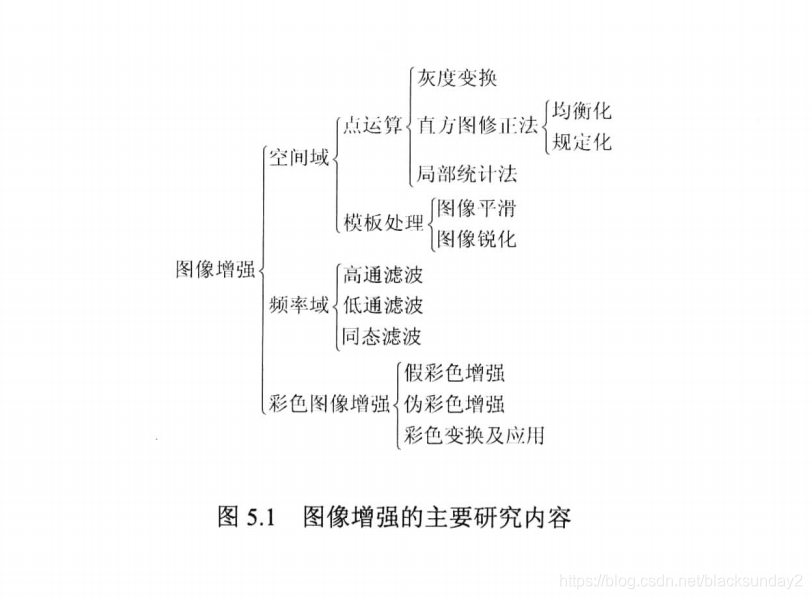
空间域方法：空间域是指图像平面自身，这类方法是以对图像的象素直接处理为基础的。

• 空间域处理：点处理，模板处理即邻域处理。

点处理是作用于单个像素的空间域处理方法，包括图像灰度变换、直方图处理、伪彩色处理等技术；

	·灰度线性变换：将曝光不足的图像中每一个像素灰度做线性拉伸
    ·分段线性变换：突出关注目标所在的灰度区间，相对抑制那些不受关注的灰度区间        
    ·反转变换：适用于增强嵌入于图像暗色区域的白色或灰色细节,特别是当黑色面积占主导地位时。        
    ·对数变换： 扩张数值较小的灰度范围，压缩数值较大的灰度范围 
    ·幂次变换：幂次变换通过幂次曲线中的值把输入的窄带值映射到宽带输出值。当时，把输入的窄带暗值映射到宽带输出亮值；当时，把输入的窄带高值映射为宽带输出亮值。        

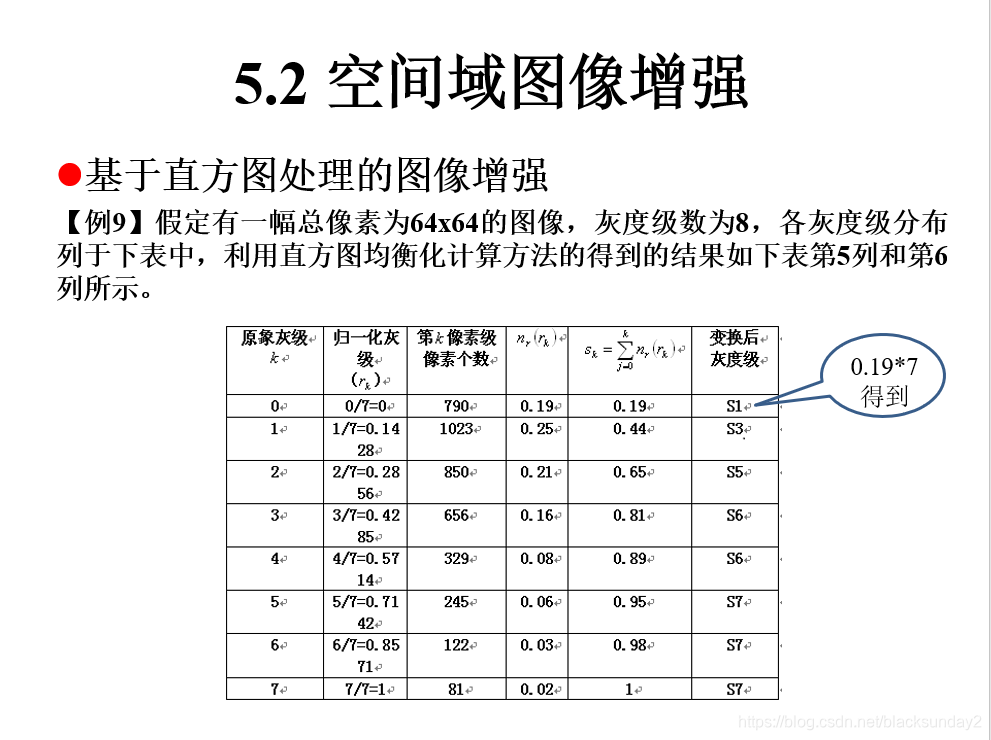
• 基于直方图处理的图像增强(可作为预处理)

灰度级直方图是图像的一种统计表达，它反映了该图中不同灰度级出现的统计概率。
直方图均衡化的目的就是寻找一个灰度变换函数T，使变化后的灰度值满足s=T®，其中0≤s ≤ 1，建立r与s之间的映射关系，要求处理后图像灰度分布的概率密度函数ps(s)=1，即变换后概率密度为[0,1]上的均匀分布，期望所有灰度级出现概率相同。


模板处理是作用于像素邻域的处理方法，包括空域平滑、空域锐化等技术。

空间域滤波要点：

·空间滤波器由（1）一个邻域（典型地是一个较小的矩形），（2）对该邻域包围的图像像素执行的预定义操作组成。
·滤波产生一个新像素，新像素的坐标等于邻域中心的坐标，像素的值是滤波操作的结果。滤波器的中心访问输入图像的每个像素，就产生了处理（滤波）后的图像.
·如果在图像像素上执行的是线性操作，则该滤波器称为线性空间滤波器。否则，滤波器就成为非线性空间滤波器。

边界处理：
·除了给定值部分，其他部分的像素值都是0
·没有指定的部分用图像边界的值进行拓展
·认为图像是周期性的
·边界不计算，输出会比原图像要小

空间域滤波增强：
要点：

·空间域滤波增强采用模板处理方法对图像进行滤波，以去除图像噪声或增强图像的细节。
·空间域滤波增强时，模板的中心从一个像素向另一个像素移动，通过模板运算得到该点的输出，常用模板是一个3x3的二维阵列，模板的系数值决定了处理的性质，如图像平滑或锐化等。

为了抑制噪声改善图像质量所进行的处理称图像平滑或去噪。
平滑滤波主要包括：局部平滑法；空间低通滤波法。
局部平滑法原理 (通过积分过程使得图像边缘模糊)：用邻域内各像素的灰度平均值代替该像素原来的灰度值；
特点：邻域越大，去噪能力越强，同时模糊程度越严重。(会使图像边缘和细节更模糊)
空间低通滤波法原理：
* 掩模不同，中心点或邻域的重要程度也不相同，因此，应根据问题的需要选取合适的掩模。
* 但不管什么样的掩模，必须保证全部权系数之和为单位值，这样可保证输出图像灰度值在许可范围内，不会出现“溢出”现象。

利用掩模卷积运算，主要步骤为：

	* 将模板在图像中沿着x方向或y方向滑动，并将模板中心与图中某个象素位置重合
	* 将模板上系数与模板下对应象素相乘
	* 将所有乘积相加求和
	* 将和（模板的输出响应）赋给图中对应模板中心位置的象素

图像锐化( 通过微分增强图像的边缘或轮廓)：
一阶导：Prewiit算子、Sobel算子
二阶导：拉普拉斯算子
·频率域方法：频率域处理技术是以修改图像的傅里叶变换为基础的。
基本思想：通过傅里叶变换，把空间域混叠的成分在频率域中分离开来，从而提取或滤去相应的图像。

频率域处理：高、低通滤波，同态滤波等。

这里，先介绍一下傅里叶，傅里叶变换可以看作是数学上的棱镜，将函数基于频率分解为不同的成分。从纯粹的数学意义上看，傅立叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看，傅立叶变换是将图像从空间域转换到频率域。

傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数

傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。思考：由于空间是三维的，图像是二维的，因此空间中物体在另一个维度上的关系就由梯度来表示，这样我们可以通过观察图像得知物体在三维空间中的对应关系。为什么要用梯度？因为实际上对图像进行二维傅立叶变换得到频谱图，就是图像梯度的分布图。