【算法基础】高精度加减乘除法

目录

高精度加法

高精度减法

高精度乘法

高精度除法

总结 

---

高精度加法

题目链接：P1601 A+B Problem（高精） - 洛谷

总的思想就是模拟列竖式的加法运算。

1）字符串的形式读入两个数据。

2）分别把这两个数据的每一位拆分，然后逆序存到数组中。

3）数组中的对应位相加然后将结果存到结果数组中的相应位置上，同时处理进位。

4）逆序输出结果数组中的值。

这里顺带说明一下数组要开多大，也就是下面代码中N要定为多大的值。高精度加减乘除法都是一样的道理。

比如高精度加法中，数据大小不超过10^500，那么开501个长度就够用了。个位为10^0，十位为10^1，百位为10^2，长度为三的数组可以表示到999，所以3位长度已经足以表示不超过10^2的数了，进而501个长度也足以表示不超过10^500的数了。当然，我们也可以开大一点，N = 1e6 + 10，这样就绝对完全够用了。

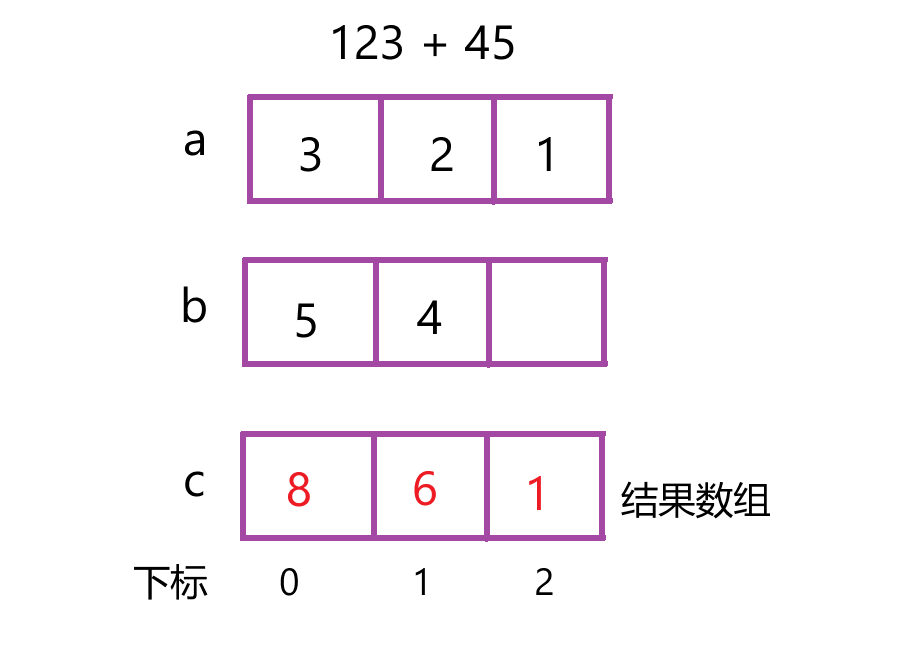
逆序存入数组的方法：假设数组a的长度为la，那么字符串s“123”中 i 位置对应存放到的数组a中位置是 a[ la - i - 1] = s[ i ] - '0'；其他的字符串逆序存放入数组的方法也是这样。

#include <iostream>
#include <string>

using namespace std;

const int N = 510;
int a[N], b[N], c[N];//a、b数组用来存输入的数据，c数组存储结果
int la, lb, lc;//分别为a、b、c数组的长度

void Add()
{
    for (int i = 0; i < lc; i++)
    {
        c[i] += a[i] + b[i];//避免覆盖原来的值
        c[i + 1] += c[i] / 10;
        c[i] %= 10;
    }
    if (c[lc] != 0) lc++;//可能多一位，而且也只可能多一位：两个个位数相加得到一个两位数的情况
}
int main()
{
    string s1, s2;
    cin >> s1 >> s2;

    la = s1.size(), lb = s2.size(), lc = max(la, lb);
    //逆序存放到数组中
    for (int i = 0; i < la; i++) a[la - 1 - i] = s1[i] - '0';
    for (int i = 0; i < lb; i++) b[lb - 1 - i] = s2[i] - '0';

    Add();

    for (int i = lc - 1; i >= 0; i--) cout << c[i];

    return 0;
}

高精度减法

题目链接：P2142 高精度减法 - 洛谷

高精度减法和加法很类似，也是去模拟。不同点就在于相减可能有负数，需要特殊处理。

1）以字符串的形式读入两个数据，字符串为s1,s2。

2）如果被减数s1 < 减数s2，那么交换s1和s2(swap），然后输出一个负号。总之确保是大的减小的。

3）将字符串的每一位拆分，然后逆序存放到数组中。方法和高精度加法用到的一样。

4）对应位置相减，然后将结果存放到结果数组的相应位置上。

5）判断是否需要借位。因为对应位相减的结果可能为负，也就是说要借位。

6）处理前导零。

7）逆序输出结果数组中的元素。

不要补充的一点是：如何比较两个字符串转化为数字后的大小。

1）如果长度不相等，长度长的字符串对应的数字大。

2）如果长度相等，直接可以用strcmp的方法来比，即相同位置，谁大，谁对应的字符串就大。

#include <iostream>
#include <string>

using namespace std;

const int N = 1e6 + 10;
int a[N], b[N], c[N];//数组c存放结果
int la, lb, lc;//数组a、b、c的长度

bool Cmp(const string &s1, const string &s2)
{
    if(s1.size() != s2.size()) return s1.size() < s2.size();
    return s1 < s2;
}

void Sub()
{
    for(int i = 0; i < lc; i++)
    {
        c[i] += a[i] - b[i];
        //判断是否需要借位
        if(c[i] < 0)
        {
            c[i + 1]--;
            c[i] += 10;
        }
    }
    //处理前导零
    while(lc > 1 && c[lc - 1] == 0) lc--;
}

int main()
{
    string s1, s2;
    cin >> s1 >> s2;
    if(Cmp(s1, s2))
    {
        swap(s1, s2);
        cout << "-";
    }

    //将每一位逆序存放到数组中
    la = s1.size(), lb = s2.size(), lc = max(la, lb);
    for(int i = 0; i < la; i++) a[la - i - 1] = s1[i] - '0';
    for(int i = 0; i < lb; i++) b[lb - i - 1] = s2[i] - '0';

    Sub();

    //逆序输出结果
    for(int i = lc - 1; i >= 0; i--) cout << c[i];
    
    return 0;
}

高精度乘法

题目链接：P1303 A*B Problem - 洛谷

无进位相乘，最后再处理进位。

1）以字符串的形式读入两个字符串。

2）分别将这两个字符串中的每一位逆序存放在数组中，逆序的方法和高精度加减法一样。

3）分别将每一位进行相乘，然后直接将结果放到相应的位置上，这个相应的位置下面会解释哈。

4）处理进位。

5）处理前导零。

6）逆序输出结果数组中的元素。

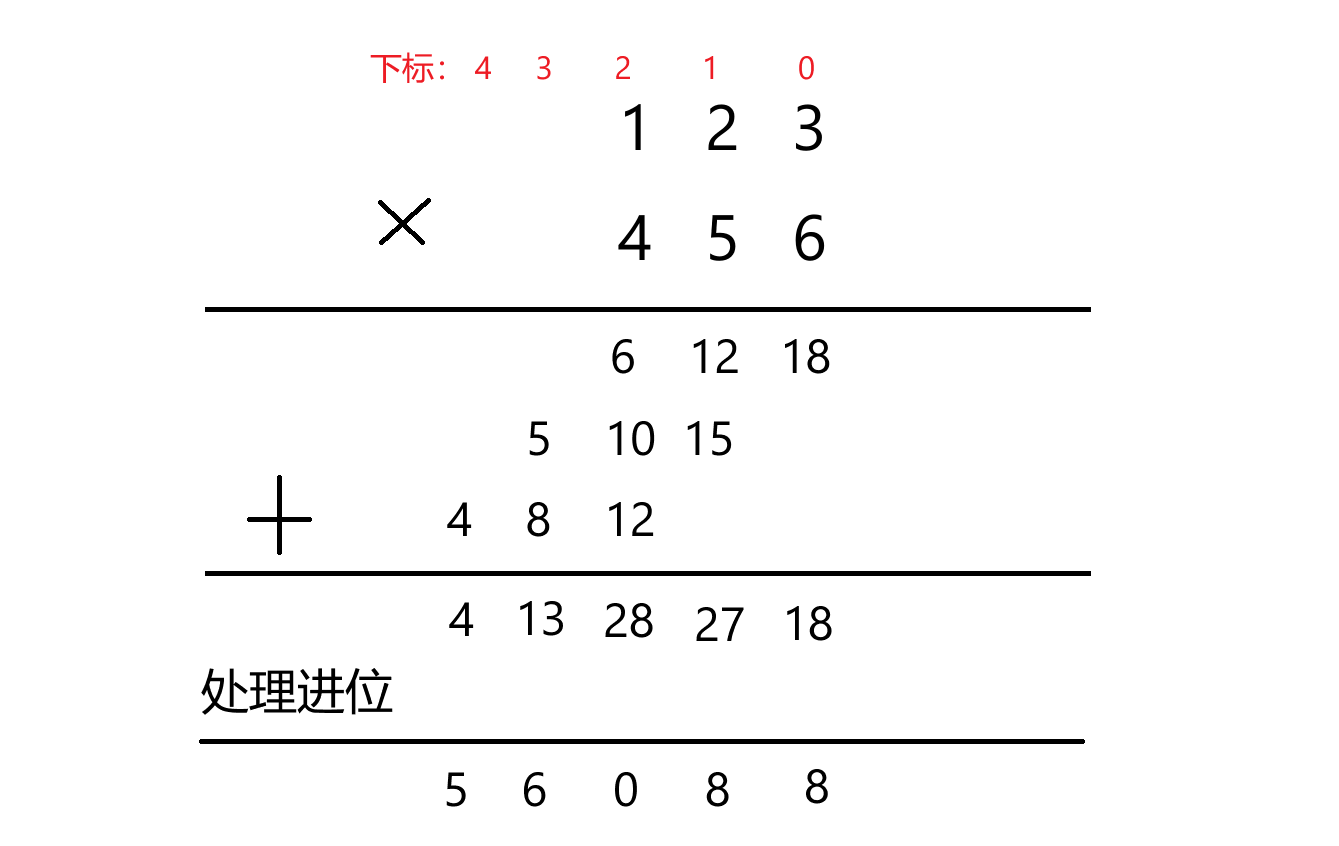
假设第一个字符串“123”的下标用 i 表示，第二个字符串“456”的下标用 j 表示，那么s1[ i ] * s2[ j ] 的结果应该存放到结果数组中下标为 i + j 的位置上。比如上图中的 4 * 1，4和1对应的下标都是2，那么它们相乘的结果就存放到结果数组中下标为4的位置。顺便说一下，为什么上图中的下标是递减的。因为我们是将这两个字符串的每一位拆分后逆序存放到数组中的，高位的1就跑到了数组的尾部。 

#include <iostream>
#include <string>

using namespace std;

const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;

//无进位相乘在相加，最后处理进位和前导零
void Mul()
{
    //无进位相乘然后相加
    for(int i = 0; i < la; i++)
    {
        for(int j = 0; j < lb; j++)
        {
            c[i + j] += a[i] * b[j];//+=避免覆盖原数字
        }
    }
    //处理进位
    for(int i = 0; i < lc; i++)
    {
        c[i + 1] += c[i] / 10;
        c[i] %= 10;
    }
    //处理前导零
    while(lc > 1 && c[lc - 1] == 0) lc--;
}
int main()
{
    string s1, s2;
    cin >> s1 >> s2;
    la = s1.size(), lb = s2.size(), lc = la + lb;//乘积的位数最多为两个乘数的位数相加
    //把字符串的每一位拆分后逆序存放到数组中
    for(int i = 0; i < la; i++) a[la - i - 1] = s1[i] - '0';
    for(int i = 0; i < lb; i++) b[lb - i - 1] = s2[i] - '0';

    Mul();

    //逆序输出结果数组
    for(int i = lc - 1; i >= 0; i--) cout << c[i];
    
    return 0;
}

高精度除法

题目链接：P1480 A/B Problem - 洛谷

高精度除法和上面的加法减法乘法有一点点不一样，但是归根结底还是在模拟。

这里的高精度除法是高精度除以低精度的，也就是说第二个数（除数）不用转为字符串，因为除数不会很大。高精度除以高进度的除法比较少见。

1）以字符串的形式读入被除数（第一个数），除数正常以整形读入。

2）将字符串中的每一位拆分然后逆序存放到数组中。方法和前面几种高精度一样。

3）模拟除法过程。

4）处理前导零。

5）逆序输出结果数组中的元素。

 看上面的红色式子，求得余数后用余数去除除数，然后把除得的商加入到结果中，除得的余数继续和下一位组合，然后再除除数。这样循环就可以求得结果。假设一开始余数t = 0。每次除完后余数和下一位组合的和的公式位 t * 10 + 下一位。比如上面的1 * 10 + 2（下一位） = 12，然后在用这个数去除。

可以看到除法是从最高位开始一一试除的，和加减乘法不一样。这是需要注意的点。

#include <iostream>
#include <string>

using namespace std;

const int N = 1e6 + 10;
int a[N], b, c[N];
int la, lc;

void div()
{
    long long t = 0;
    //除法是从高位开始试除的，与前面的加减乘法不一样
    for(int i = la - 1; i >= 0; i--)
    {
        t = t * 10 + a[i];//求余数
        c[i] = t / b;//求商然后加入答案
        t %= b;//更新余数为商后的余数
    }
    while(lc > 1 && c[lc - 1] == 0) lc--;//处理前导零
}
int main()
{
    string s;
    cin >> s >> b;
    la = s.size();
    lc = la;
    //拆分每一位逆序存放到数组中
    for(int i = 0; i < la; i++) a[la - 1 - i] = s[i] - '0';
    
    div();
    
    //逆序输出结果
    for(int i = lc - 1; i >= 0; i--) cout << c[i];
    
    return 0;
}

总结 

通过上述的代码，我们可以看到高精度的做法都是在模拟，而且代码也极为相似或者说逻辑上很相似。但高精度的解法肯定不止上面的，比如高精度加法，还有好几种解法，这里就不提啦。最后，感谢支持！