PTA----字母子集合

最近刷题遇见一个不错的题，分享一下！

 

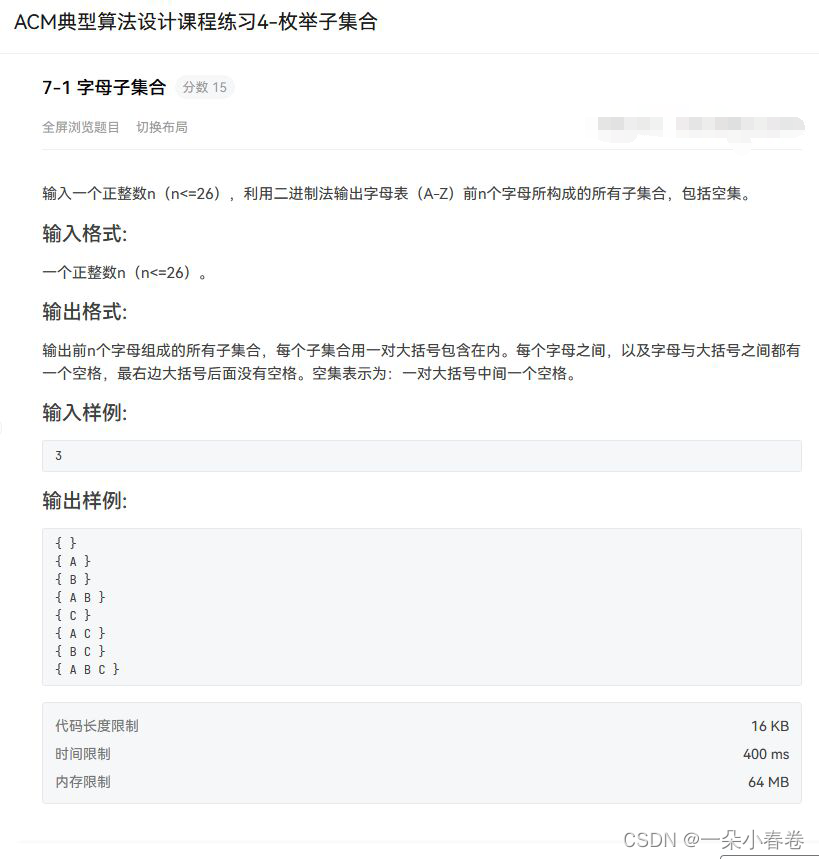
这题啥意思呢？先写一个数组存A-Z，输入一个数，输出它的所有子集（包括空集）如果输入3，代表A, B, C的所有子集，并用他们三个表示。

#define _CRT_SECURE_NO_WARNINGS 1

#include <stdio.h>
void my_print(char a1[], int count)

{
    int i, j, tmp;
    int Sum = 1 << count;          // 子集合的个数
    for (i = 0; i < Sum; i++)
    {
        j = i;
        tmp = 0;
        printf("{");
        while (j)
        {
            if (j & 1)   //按位与运算
            {
                printf(" %c", a1[tmp]);   //打印字母
            }
            j >>= 1;
            tmp++;
        }

        printf(" }\n");
    }
}
int main()
{
    char a[26] = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
    int num;
    scanf("%d", &num);
    my_print(a, num);

    return 0;

}

咱来具体看一下-------

输入2，那他的子集有 0（代表空集） ，A,  B,  AB四个对吧。

Sum代表子集个数，Sum=1<<2(1左移2)变成4，所以运行4次

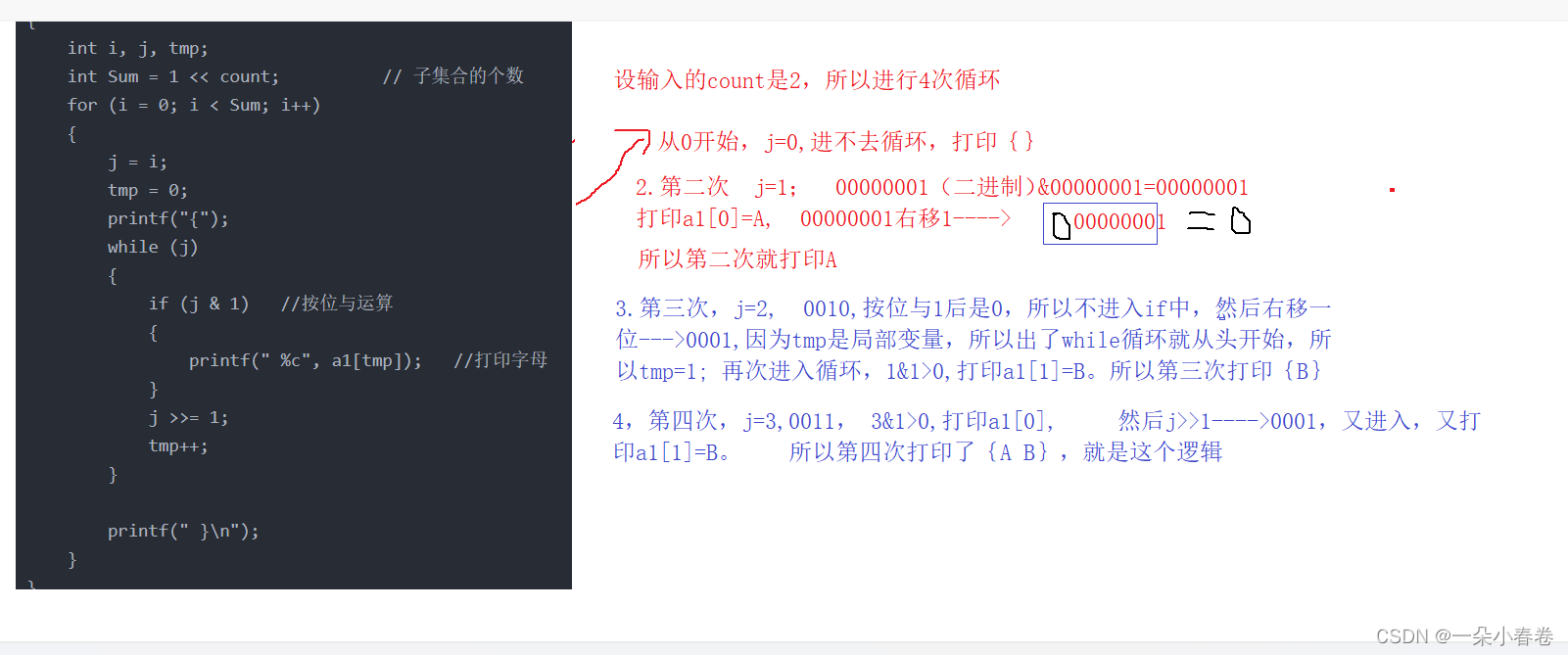
同理，输入3和2的逻辑一模一样。