动态数组基础

许多程序需要存储和处理相同类型的元素序列，例如数字、字符串，甚至是更复杂的对象。数组是一种广泛使用的结构，用于表示此类数据序列，因为可以通过索引在常数时间内访问元素。然而，普通数组有一个显著的限制——它们的大小是固定的。这使得在元素数量事先未知的情况下无法创建数组。在这种情况下，使用动态数组是一个可行的解决方案。

核心概念

动态数组是一种线性数据结构，能够在其大小变化时增长，有时甚至缩小。通常，它内部有一个实际存储数据的常规数组，并在此基础上提供一些额外的操作。

动态数组有两个重要属性：

• 大小 (size)：指已经存储在其中的元素数量；
• 容量 (capacity)：指可能存储的元素数量，对应于内部常规数组的大小。

通常有两种方式：要么为新的动态数组指定一个容量，要么设置一个常量默认值（例如10）。与基本数组不同，动态数组提供了在任意位置添加/删除元素的操作。这样，我们可以在创建动态数组后逐个添加和删除元素。

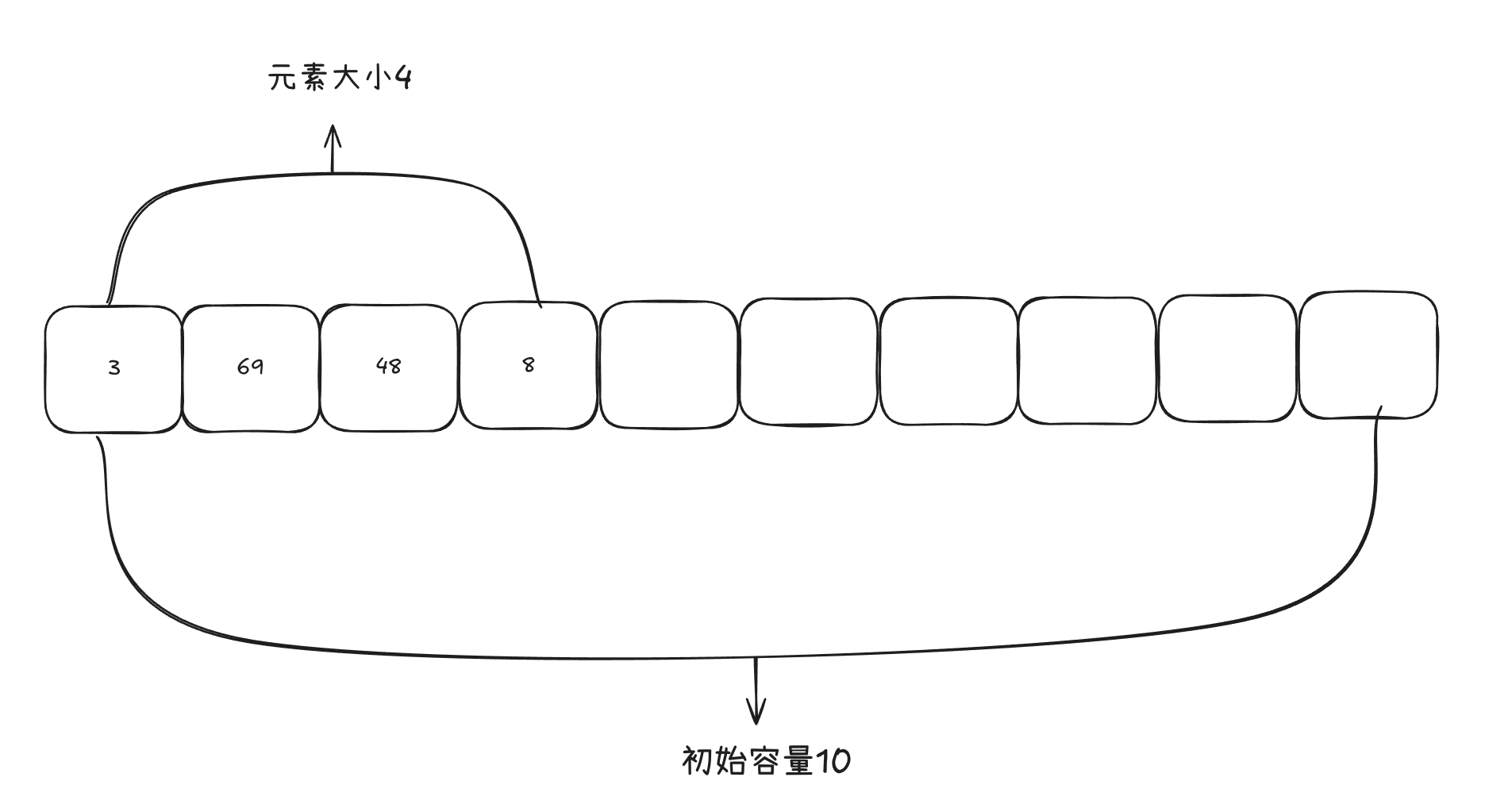
下图展示了一个添加了四个数字的动态数组。实际大小为4，容量为10（初始状态）：

动态数组：大小与容量

扩展因子 (Scaling factor)

如果元素数量超过容量，所有元素将被复制到一个更大的新内部数组中。对于新数组的大小，有多种不同的扩展策略。最常见的策略是将初始容量乘以1.5（Java）或2（C++，GCC STL实现）。还有一些更独特的情况，例如Go语言的动态数组（“切片”），在元素数量达到1024之前会将大小翻倍，之后比例变为5/4。

这在时间和空间复杂度之间是一种权衡。使用更大的增长因子，我们可以在需要扩展数组之前进行更多的插入操作，从而降低时间复杂度。

但什么是最佳的扩展因子呢？即，哪个值能同时实现最优的时间和空间复杂度？事实证明，这个值应该等于黄金比例，1.61803。如你所见，1.5已经非常接近这个值了。

当删除元素时，也可能需要支持内部数组的缩小，以减少所需的内存大小。

常见操作

• 在数组末尾添加元素：如上所述，在一般情况下，当我们只需将元素添加到数组末尾（不指定索引）时，其复杂度如下：

  • O(1)：在平均情况下，因为我们只是将元素插入到已分配的内存中（元素数量小于容量）；
  • O(n)：在最坏情况下，当我们耗尽空间，需要分配一个新数组并将所有元素复制进去。 在数组末尾添加元素的平均估计值称为摊销 (amortized)。由于很难一眼看出它是O(1)，我们需要使用一种特殊的分析方法。

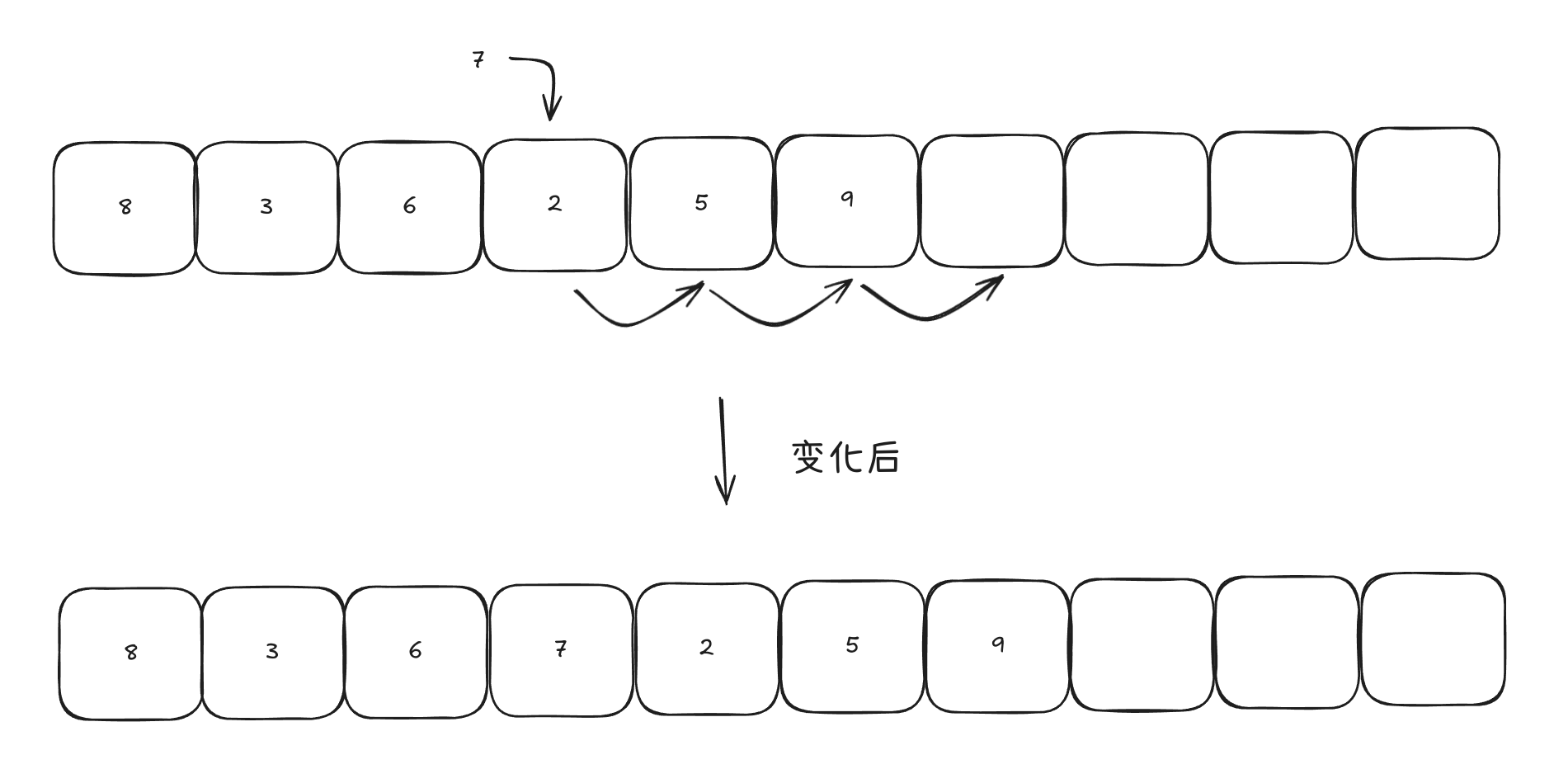
• 在指定索引处添加元素：此操作用于在已放置的元素之间插入一个新元素。其复杂度（平均和最坏情况）均为O(n)，因为每次插入时，我们必须将目标索引处的元素以及之后的所有元素向右移动一个位置。
  

• 在指定索引处更新值：此操作用另一个元素替换指定索引处的元素。这一切都在常数时间内完成，因为它就像基本数组中的赋值操作，因此其复杂度均为O(1)。

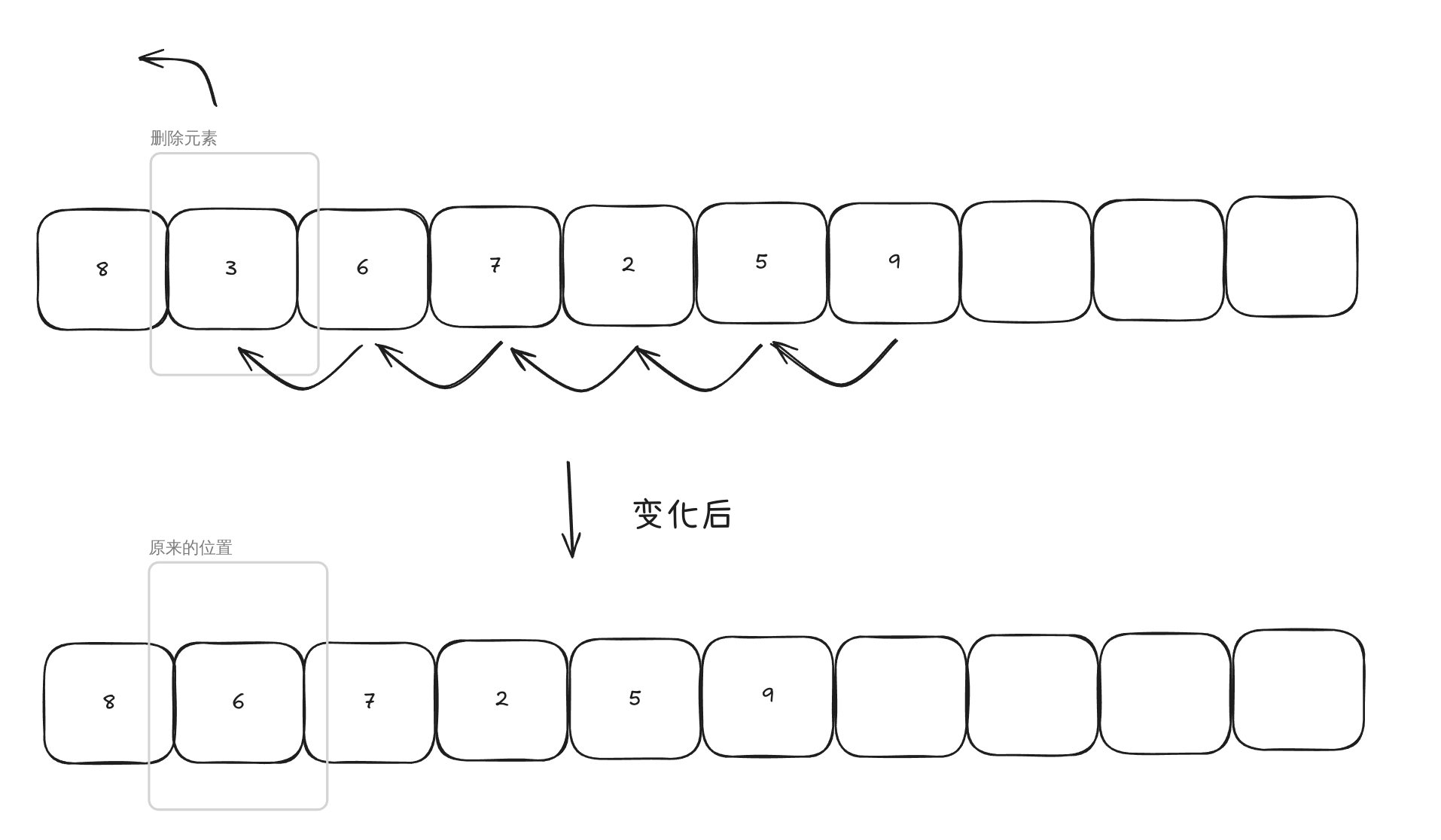
• 按值/索引删除元素：这些方法要么删除指定的第一个元素，要么删除指定索引处的元素。它们与在指定索引处添加元素类似，因为我们需要将剩余的一些（或全部）元素向左移动一个位置；因此，它们的复杂度也为O(n)。
  

• 清空 (Clear)：这里我们只想删除数组中的所有元素。由于插入是通过计算当前数组大小来完成的，我们可以直接将大小重置为零，并在后续插入时覆盖旧元素。这会使旧元素在内存中“悬挂”（因此垃圾回收器无法立即回收它们），直到它们被覆盖。最简单的实现复杂度为O(1)，但正确的实现应为O(n)。

• 按索引获取元素：由于动态数组本质上只是一个普通数组，我们可以以常数时间通过索引访问元素，因此其复杂度为O(1)。

结论

动态数组就像一个常规数组，但存储的元素数量可以改变。如果添加操作导致没有足够的空间存储元素，就会分配一个新的更大的数组，并将旧数组的每个元素复制到新数组中。扩展因子是时间（速度）和空间之间的一种权衡。使用更大的因子，我们会有更少的分配和复制操作，但浪费内存的可能性更高。最常见的因子是1.5和2。在某些实现中，动态数组可以支持缩小，以在删除元素后减少使用的内存。

---

外部链接

摊销分析