算法与数据结构

最新推荐文章于 2025-01-12 18:46:37 发布

Elon0

最新推荐文章于 2025-01-12 18:46:37 发布

阅读量149

点赞数

CC 4.0 BY-SA版权

分类专栏：算法

本文链接：https://blog.youkuaiyun.com/biggoodloong/article/details/88388957

算法专栏收录该内容

10 篇文章

订阅专栏

选择排序

假设排序从小到大，每次从未排序的子序列中找出最小的值，与这个子序列第一个值交换，i++；

template<typename T>
void selectionSort(T arr[], int n){

    for(int i = 0 ; i < n ; i ++){

        int minIndex = i;
        for( int j = i + 1 ; j < n ; j ++ )
            if( arr[j] < arr[minIndex] )
                minIndex = j;

        swap( arr[i] , arr[minIndex] );
    }
}

插入排序

每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子序列中，直到全部记录插入完成。

插入排序包括：直接插入排序，折半插入排序和希尔排序。

template<typename T>
void insertionSort(T arr[], int n){

    for( int i = 1 ; i < n ; i ++ ) {

        // 寻找元素arr[i]合适的插入位置
        // 写法1
//        for( int j = i ; j > 0 ; j-- )
//            if( arr[j] < arr[j-1] )
//                swap( arr[j] , arr[j-1] );
//            else
//                break;

        // 写法2
//        for( int j = i ; j > 0 && arr[j] < arr[j-1] ; j -- )
//            swap( arr[j] , arr[j-1] );

        // 写法3
        T e = arr[i];
        int j; // j保存元素e应该插入的位置
        for (j = i; j > 0 && arr[j-1] > e; j--)
            arr[j] = arr[j-1];
        arr[j] = e;
    }

    return;
}

归并排序

// 将arr[l...mid]和arr[mid+1...r]两部分进行归并
template<typename  T>
void __merge(T arr[], int l, int mid, int r){

    //* VS不支持动态长度数组, 即不能使用 T aux[r-l+1]的方式申请aux的空间
    //* 使用VS的同学, 请使用new的方式申请aux空间
    //* 使用new申请空间, 不要忘了在__merge函数的最后, delete掉申请的空间:)
    T aux[r-l+1];
    //T *aux = new T[r-l+1];

    for( int i = l ; i <= r; i ++ )
        aux[i-l] = arr[i];

    // 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
    int i = l, j = mid+1;
    for( int k = l ; k <= r; k ++ ){

        if( i > mid ){  // 如果左半部分元素已经全部处理完毕
            arr[k] = aux[j-l]; j ++;
        }
        else if( j > r ){  // 如果右半部分元素已经全部处理完毕
            arr[k] = aux[i-l]; i ++;
        }
        else if( aux[i-l] < aux[j-l] ) {  // 左半部分所指元素 < 右半部分所指元素
            arr[k] = aux[i-l]; i ++;
        }
        else{  // 左半部分所指元素 >= 右半部分所指元素
            arr[k] = aux[j-l]; j ++;
        }
    }

    //delete[] aux;
}

// 递归使用归并排序,对arr[l...r]的范围进行排序
template<typename T>
void __mergeSort(T arr[], int l, int r){

    if( l >= r )
        return;

    int mid = (l+r)/2;
    __mergeSort(arr, l, mid);
    __mergeSort(arr, mid+1, r);
    __merge(arr, l, mid, r);
}

template<typename T>
void mergeSort(T arr[], int n){

    __mergeSort( arr , 0 , n-1 );
}

归并排序优化

// 使用优化的归并排序算法, 对arr[l...r]的范围进行排序
template<typename T>
void __mergeSort2(T arr[], int l, int r){

    // 优化2: 对于小规模数组, 使用插入排序
    if( r - l <= 15 ){
        insertionSort(arr, l, r);
        return;
    }

    int mid = (l+r)/2;
    __mergeSort2(arr, l, mid);
    __mergeSort2(arr, mid+1, r);

    // 优化1: 对于arr[mid] <= arr[mid+1]的情况,不进行merge
    // 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失
    if( arr[mid] > arr[mid+1] )
        __merge(arr, l, mid, r);
}

template<typename T>
void mergeSort2(T arr[], int n){

    __mergeSort2( arr , 0 , n-1 );
}

快速排序

// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template <typename T>
int __partition(T arr[], int l, int r){

    T v = arr[l];

    int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v
    for( int i = l + 1 ; i <= r ; i ++ )
        if( arr[i] < v ){
            j ++;
            swap( arr[j] , arr[i] );
        }

    swap( arr[l] , arr[j]);

    return j;
}

// 对arr[l...r]部分进行快速排序
template <typename T>
void __quickSort(T arr[], int l, int r){

    if( l >= r )
        return;

    int p = __partition(arr, l, r);
    __quickSort(arr, l, p-1 );
    __quickSort(arr, p+1, r);
}

template <typename T>
void quickSort(T arr[], int n){

    __quickSort(arr, 0, n-1);
}

优化1

对近乎有序的数组

// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template <typename T>
int _partition(T arr[], int l, int r){

    // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
    swap( arr[l] , arr[rand()%(r-l+1)+l] );

    T v = arr[l];
    int j = l;
    for( int i = l + 1 ; i <= r ; i ++ )
        if( arr[i] < v ){
            j ++;
            swap( arr[j] , arr[i] );
        }

    swap( arr[l] , arr[j]);

    return j;
}

// 对arr[l...r]部分进行快速排序
template <typename T>
void _quickSort(T arr[], int l, int r){

    // 对于小规模数组, 使用插入排序进行优化
    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;
    }

    int p = _partition(arr, l, r);
    _quickSort(arr, l, p-1 );
    _quickSort(arr, p+1, r);
}

template <typename T>
void quickSort(T arr[], int n){

    srand(time(NULL));
    _quickSort(arr, 0, n-1);
}

优化2

避免包含大量重复值，双路快排

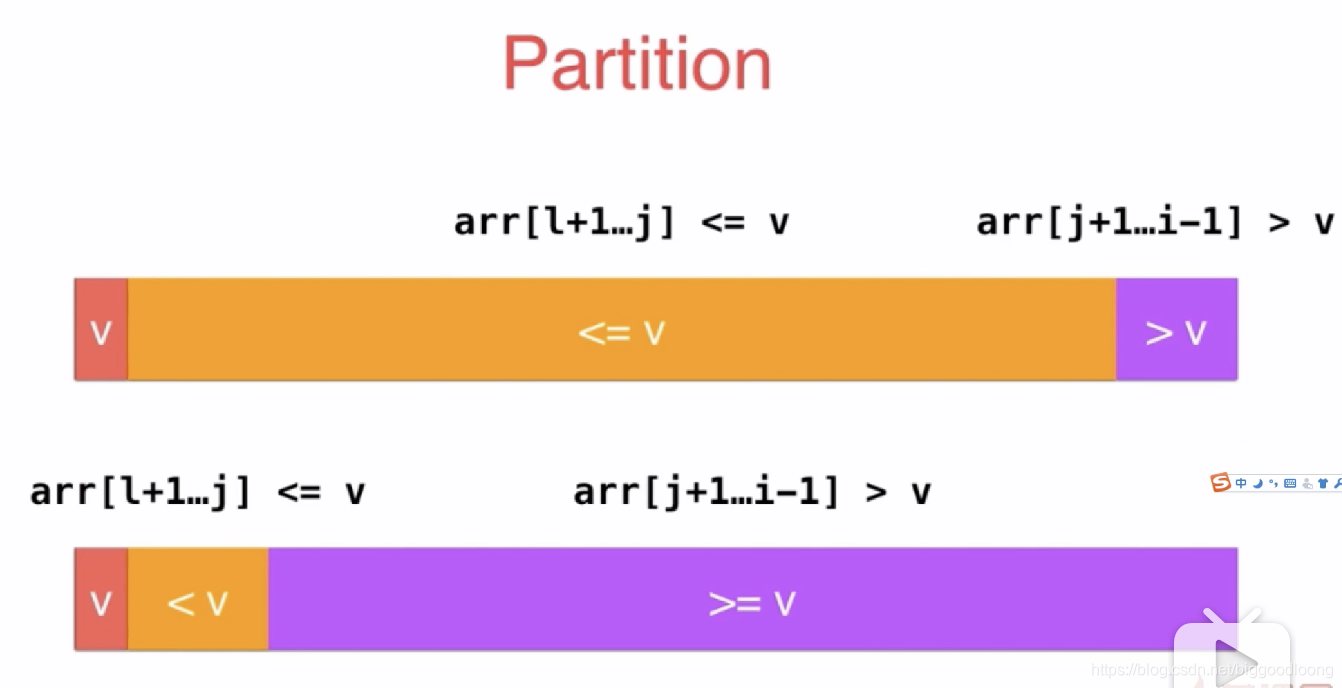
// 双路快速排序的partition
// 返回p, 使得arr[l...p-1] <= arr[p] ; arr[p+1...r] >= arr[p]
// 双路快排处理的元素正好等于arr[p]的时候要注意，详见下面的注释：）
template <typename T>
int _partition2(T arr[], int l, int r){

    // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
    swap( arr[l] , arr[rand()%(r-l+1)+l] );
    T v = arr[l];

    // arr[l+1...i) <= v; arr(j...r] >= v
    int i = l+1, j = r;
    while( true ){
        // 注意这里的边界, arr[i] < v, 不能是arr[i] <= v
        // 思考一下为什么?
        while( i <= r && arr[i] < v )
            i ++;

        // 注意这里的边界, arr[j] > v, 不能是arr[j] >= v
        // 思考一下为什么?
        while( j >= l+1 && arr[j] > v )
            j --;

        // 对于上面的两个边界的设定, 有的同学在课程的问答区有很好的回答:)
        // 大家可以参考: http://coding.imooc.com/learn/questiondetail/4920.html

        if( i > j )
            break;

        swap( arr[i] , arr[j] );
        i ++;
        j --;
    }

    swap( arr[l] , arr[j]);

    return j;
}

// 对arr[l...r]部分进行快速排序
template <typename T>
void _quickSort(T arr[], int l, int r){

    // 对于小规模数组, 使用插入排序进行优化
    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;
    }

    // 调用双路快速排序的partition
    int p = _partition2(arr, l, r);
    _quickSort(arr, l, p-1 );
    _quickSort(arr, p+1, r);
}

template <typename T>
void quickSort(T arr[], int n){

    srand(time(NULL));
    _quickSort(arr, 0, n-1);
}

求逆序对（归并排序）

// 将arr[l...mid]和arr[mid+1...r]两部分进行归并
long long __merge(int arr[], int l, int mid, int r){
//    T aux[r-l+1];

    int *aux = new int[r-l+1];
    for(int i=l;i<=r;i++){
        aux[i-l]=arr[i];
    }
    long long res=0;

    int i=l, j=mid+1;
    for(int k=l;k<=r;k++){
        if(i>mid){
            arr[k]=aux[j-l];j++;
        }
        else if(j>r){
            arr[k]=aux[i-1];i++;
        }
        else if(aux[i-l]<aux[j-l]){
            arr[k]=aux[i-l];
            i++;
        }else{
            arr[k]=aux[j-l];
            j++;
            res+=(long long)(mid-i+1);
        }
    }

    delete[] aux;
    return res;

}

// 求arr[l..r]范围的逆序数对个数
// 思考: 归并排序的优化可否用于求逆序数对的算法? :)
long long __inversionCount(int arr[], int l, int r){

    if( l >= r )
        return 0;

    int mid = l + (r-l)/2;

    // 求出 arr[l...mid] 范围的逆序数
    long long res1 = __inversionCount( arr, l, mid);
    // 求出 arr[mid+1...r] 范围的逆序数
    long long res2 = __inversionCount( arr, mid+1, r);

    return res1 + res2 + __merge( arr, l, mid, r);
}

// 递归求arr的逆序数对个数
long long inversionCount(int arr[], int n){

    return __inversionCount(arr, 0, n-1);
}

求第K小的数

// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template <typename T>
int __partition(T arr[], int l, int r){

    // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
    swap( arr[l] , arr[rand()%(r-l+1)+l] );

    T v = arr[l];
    int j = l;
    for( int i = l + 1 ; i <= r ; i ++ )
        if( arr[i] < v ){
            j ++;
            swap( arr[j] , arr[i] );
        }

    swap( arr[l] , arr[j]);

    return j;
}

// 对arr[l...r]部分进行快速排序
template <typename T>
int _quickSort(T arr[], int l, int r, int k){

    if(r==l)
        return arr[l];

    int p = __partition(arr, l, r);
    if(k<p){
        return _quickSort(arr, l, p-1 ,k);
    }else if(k>p){
        return _quickSort(arr, p+1, r,k);
    }else
        return arr[p];
}

//找第k小
template <typename T>
int quickSort(T arr[], int n,int k){

    srand(time(NULL));
    return _quickSort(arr, 0, n-1, k);
}