打开题目 Constructing Roads In JGShining's Kingdom
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 23264 Accepted Submission(s): 6655
Problem Description
JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.
Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.
With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.
Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.
The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.
But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.
For example, the roads in Figure I are forbidden.
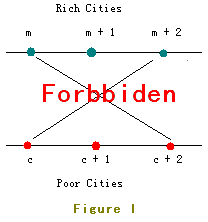
In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^
Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.
With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.
Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.
The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.
But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.
For example, the roads in Figure I are forbidden.

In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^
Input
Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to the end of file.
Output
For each test case, output the result in the form of sample.
You should tell JGShining what's the maximal number of road(s) can be built.
You should tell JGShining what's the maximal number of road(s) can be built.
Sample Input
2 1 2 2 1 3 1 2 2 3 3 1
Sample Output
Case 1: My king, at most 1 road can be built. Case 2: My king, at most 2 roads can be built.HintHuge input, scanf is recommended.
Author
JGShining(极光炫影)
Recommend
最长不减子序列,n*logn复杂度:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
const int N = 5*1e5+10;
int dp[N],a[N];
struct node {
int a,b;
} s[N];
bool cmp(node A,node B) {
if(A.a==B.a)
return A.b<B.b;
return A.a<B.a;
}
int find(int l,int r,int x) { //二分的时候不要用递归,容易超时,
while(l<=r) { //任何时候递归都是耗时间的,能不用就不用
int mid=l+r>>1;
if(dp[mid]<x)
l=mid+1;
else if(dp[mid]>x)
r=mid-1;
else {
l=mid;
break;
}
}
// printf("--\n");
return l;
}
int main() {
int n,p=0;
while(scanf("%d",&n)!=EOF) {
for(int i=0; i<n; i++) {
scanf("%d%d",&s[i].a,&s[i].b);
}
sort(s,s+n,cmp);
// for(int i=0; i<n; i++) //这段不要的,能省时间就省时间,记住
// a[i]=s[i].b;
int len=0,j;
dp[0]=-1;
for(int i=0; i<n; i++) {
if(s[i].b>=dp[len])
dp[++len]=s[i].b;
// printf("--\n");
else {
j=find(1,len,s[i].b);
dp[j]=s[i].b;
}
}
printf("Case %d:\n",++p);
if(len==1)
printf("My king, at most %d road can be built.\n\n",len);
else
printf("My king, at most %d roads can be built.\n\n",len);
}
return 0;
}






 解决在一个包含资源丰富和资源匮乏城市的王国中,如何最大化建设不交叉的道路数量的问题。采用最长不减子序列算法,确保道路连接资源互补的城市且不会相交。
解决在一个包含资源丰富和资源匮乏城市的王国中,如何最大化建设不交叉的道路数量的问题。采用最长不减子序列算法,确保道路连接资源互补的城市且不会相交。
















 1067
1067

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








