Flip Game
Time Limit : 2000/1000ms (Java/Other) Memory Limit : 131072/65536K (Java/Other)
Total Submission(s) : 7 Accepted Submission(s) : 4
Problem Description
Flip game is played on a rectangular 4x4 field with two-sided pieces placed on each of its 16 squares. One side of each piece is white and the other one is black and each piece is lying either it's black or white side up. Each round you flip 3 to 5 pieces,
thus changing the color of their upper side from black to white and vice versa. The pieces to be flipped are chosen every round according to the following rules:
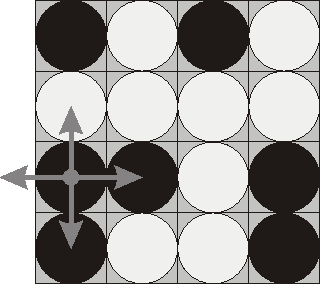 Consider the following position as an example:
Consider the following position as an example:
bwbw
wwww
bbwb
bwwb
Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.
- Choose any one of the 16 pieces.
- Flip the chosen piece and also all adjacent pieces to the left, to the right, to the top, and to the bottom of the chosen piece (if there are any).
 Consider the following position as an example:
Consider the following position as an example: bwbw
wwww
bbwb
bwwb
Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.
Input
The input consists of 4 lines with 4 characters "w" or "b" each that denote game field position.
Output
Write to the output file a single integer number - the minimum number of rounds needed to achieve the goal of the game from the given position. If the goal is initially achieved, then write 0. If it's impossible to achieve the goal, then write the word "Impossible"
(without quotes).
Sample Input
bwwb bbwb bwwb bwww
Sample Output
4
Source
PKU
题目大意:给定一棋局状态,通过规定操作(翻转某一棋子以及它四个方向的棋子)是全部棋子为白棋或黑棋,要求最小步数.
分析:简单BFS.注意状态存储是将棋局编码成一个整数(有效位为16位).
此题其实可以剪枝(每次访问一个棋局都将它对应所有的等效棋局标记,即旋转旋转旋转,延任一对角线或边平分线翻转,再旋转旋转旋转),但由于数据弱,或数据只有一组,或游戏性质的原因,此题没有剪枝也AC了.
另外,由于可以将棋局编码成一个整数,搜索时对棋局的操作也可以用对整数的操作代替.
用操作整数代替操作棋局:
#include<iostream>
#include<map>
#include<string>
#include<queue>
#include<cstdio>
#include<cstring>
using namespace std;
#define maxn 1<<16
struct NODE
{
int m;
int step;
}Q[maxn], u, t;
bool mark[maxn];
char m[4][5];
int flag;
int head, tail;
int connect[16][5] = { { 16, 15, 12, 0, 0 }, { 15, 16, 14, 11, 0 }, { 14, 15, 13, 10, 0 }, { 13, 14, 9, 0, 0 }, { 12, 16, 11, 8, 0 }, { 11, 15, 12, 10, 7 }, { 10, 14, 11, 9, 6 }, { 9, 13, 10, 5, 0 }, { 8, 12, 7, 4, 0 }, { 7, 11, 8, 6, 3 }, { 6, 10, 7, 5, 2 }, { 5, 9, 6, 1, 0 }, { 4, 8, 3, 0, 0 }, { 3, 7, 4, 2, 0 }, { 2, 6, 3, 1, 0 }, { 1, 5, 2, 0, 0 } };
int Exchange()
{
int z = 0;
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
{
z = z << 1;
if (m[i][j] == 'b')
z += 1;
}
return z;
}
int flip(int z, int j)
{
return z ^ (1 << (j - 1));
}
int Flip(struct NODE &u, int i)
{
int z = u.m;
for (int j = 0; j < 5; j++)
{
if (connect[i][j])
z = flip(z, connect[i][j]);
}
return z;
}
void BFS()
{
head = tail = 0;
t.m = Exchange(); t.step = 0;
Q[tail++] = t;
if (t.m == (1 << 16) - 1 || t.m == 0)
{
flag = 1;
return;
}
mark[t.m] = true;
while (head < tail)
{
u = Q[head++];
for (int i = 0; i < 16; i++)
{
t.m = Flip(u, i); t.step = u.step + 1;
if (mark[t.m] == false)
{
Q[tail++] = t;
if (t.m == (1 << 16) - 1 || t.m == 0)
{
flag = 1;
return;
}
mark[t.m] = true;
}
}
}
}
int main()
{
//freopen("f:\\input.txt", "r", stdin);
int i;
for (i = 0; i < 4; i++)
scanf("%s", m[i]);
memset(mark, false, sizeof(mark));
flag = 0;
BFS();
if (flag)
printf("%d\n", Q[tail - 1].step);
else
printf("Impossible\n");
return 0;
}
常规方法:
#include<iostream>
#include<map>
#include<string>
#include<queue>
#include<cstdio>
#include<cstring>
using namespace std;
#define maxn 1<<16
struct NODE
{
char m[4][4];
int step;
}Q[maxn], u, t;
bool mark[maxn];
int dx[5] = { 0, 0, -1, 0, 1 }, dy[5] = { 0, -1, 0, 1, 0 };
int flag;
int head, tail;
int z;
int Exchange(struct NODE &a)
{
int z = 0;
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
{
z = z << 1;
if (a.m[i][j] == 'b')
z += 1;
}
return z;
}
void Visit(struct NODE &a)
{
int jud = Exchange(a);
Q[tail++] = a;
if (jud == (1 << 16) - 1 || jud == 0)
{
flag = 1;
return;
}
mark[jud] = true;
}
void Update(struct NODE &u,struct NODE &a, int i, int j)
{
a = u;
for (int k = 0; k < 5; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if (0 <= x&&x < 4 && 0 <= y&&y < 4)
a.m[x][y] = (u.m[x][y] == 'b' ? 'w' : 'b');
}
a.step = u.step + 1;
}
void BFS()
{
head = tail = 0;
t.step = 0;
Q[tail++] = t;
int jud = Exchange(t);
if (jud == (1 << 16) - 1 || jud == 0)
{
flag = 1;
return;
}
mark[jud] = true;
while (head < tail)
{
u = Q[head++];
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4;j++)
{
Update(u,t, i,j);
int jud = Exchange(t);
if (mark[jud] == false)
{
Q[tail++] = t;
if (jud == (1 << 16) - 1 || jud == 0)
{
flag = 1;
return;
}
mark[jud] = true;
}
}
}
}
int main()
{
freopen("f:\\input.txt", "r", stdin);
int i, j;
for (i = 0; i < 4; i++)
scanf("%s", &t.m[i]);
memset(mark, false, sizeof(mark));
flag = 0;
BFS();
if (flag)
printf("%d\n", Q[tail - 1].step);
else
printf("Impossible\n");
return 0;
}





 本文介绍了一种使用广度优先搜索(BFS)算法解决FlipGame问题的方法,目标是在最少的步骤内使所有棋子颜色统一。文章提供了两种实现思路:一种是通过整数操作简化搜索过程;另一种则是直接操作棋盘状态。
本文介绍了一种使用广度优先搜索(BFS)算法解决FlipGame问题的方法,目标是在最少的步骤内使所有棋子颜色统一。文章提供了两种实现思路:一种是通过整数操作简化搜索过程;另一种则是直接操作棋盘状态。
















 488
488

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








