一些简单的算法

几种基础的排序算法

一、冒泡排序BubbleSort

	static void bubbleSort(int[] arr){
        for(int i = 0;i<arr.length-1;i++){
            for(int j = 0;j <arr.length-i-1;j++){
                if(arr[j]>arr[j+1]){
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
        }
    }

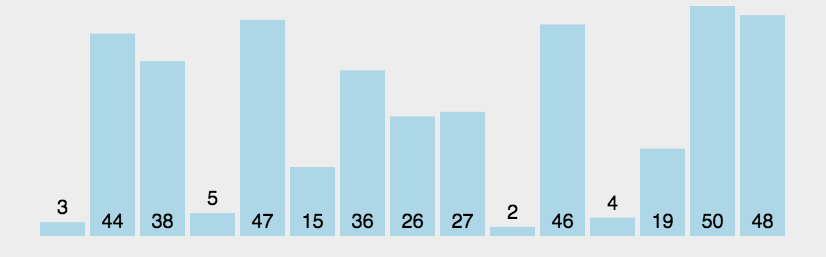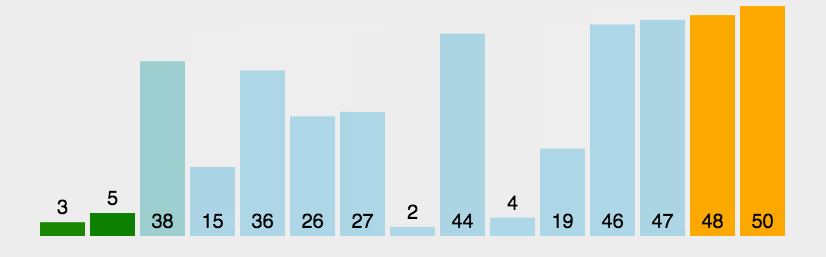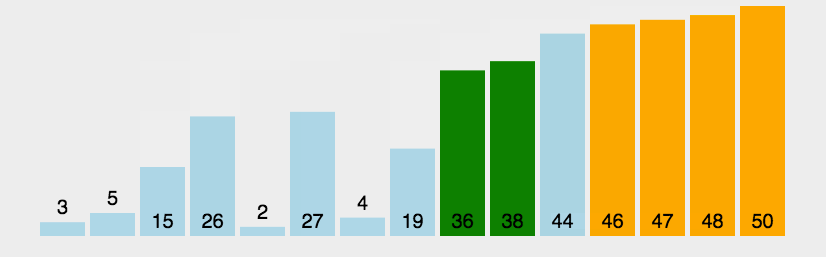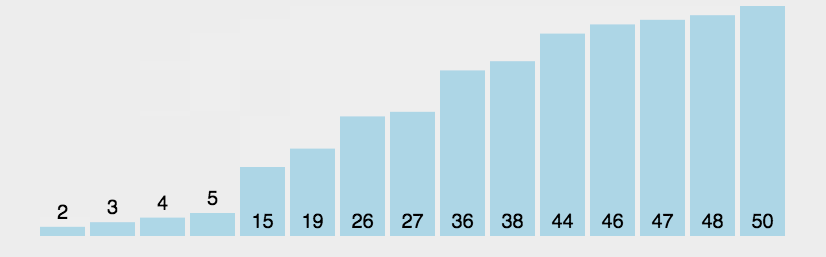
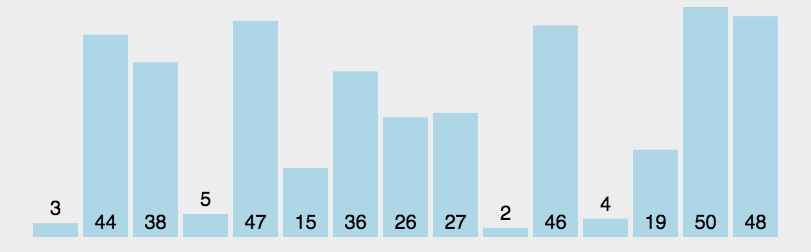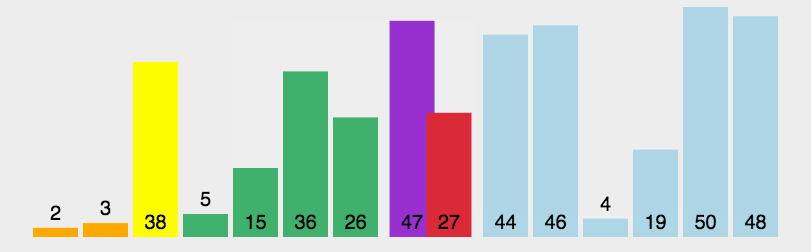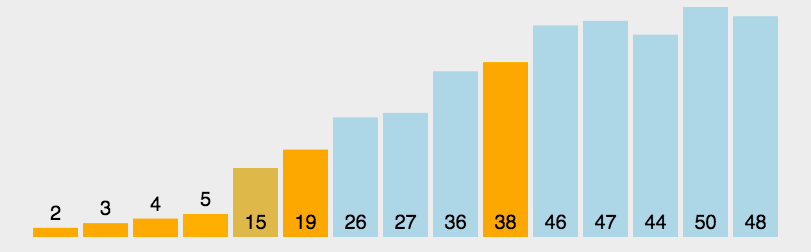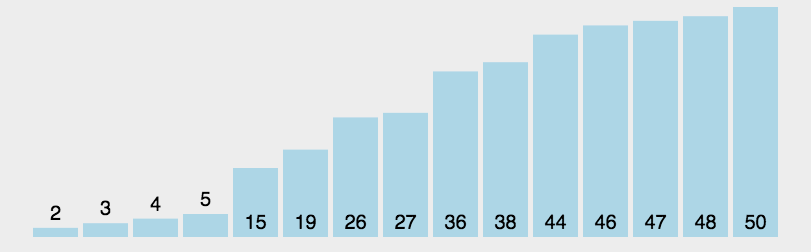
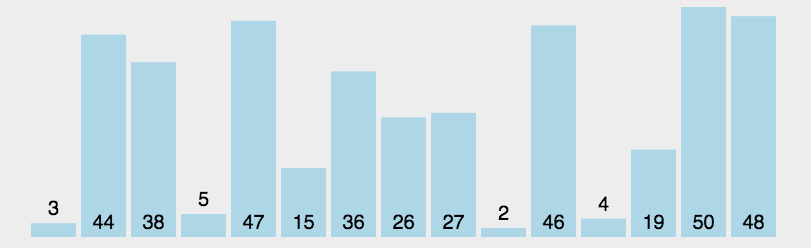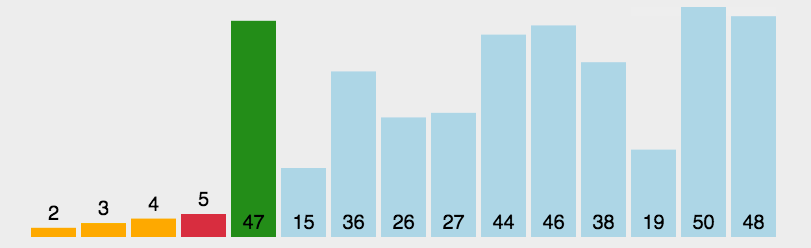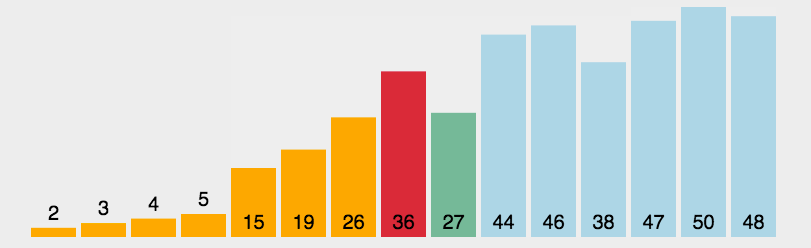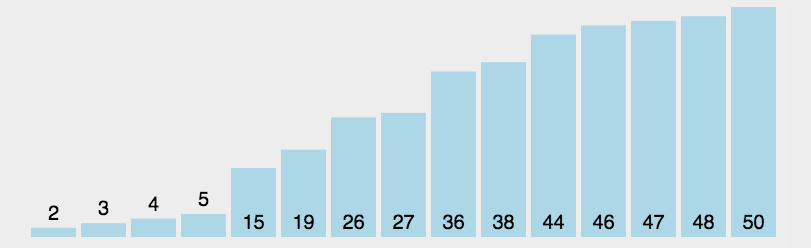
二、快速排序QuickSort

基本思路：

• 将数组划分为两个子数组A[start,end-1] A[start+1,end]，使得A[start]为大小居中的数，左侧都小于A[start]，右侧都大于A[end],通过递归调用快速排序对子数组进行排序。

• 1.需要形参有开头start和结尾end

• 2.如果start < end就递归自己
• 3.把下标为0（也可以是其他下标）的值设为标准值
• 把开头和结束分别设置为低位（low）和高位（high）
• 4.当low<high时循环执行
• 1.（low<high时)高位的值大于标准值，把高位减一位，直到小于时把当前高位的值赋值给低位
• 2.（low<high时)低位的值小于标准值，把低位减一位，直到大于时把当前低位的值赋值给高位
• 5.执行完后此时的高位和低位相等，把标准值赋值给低位or高位的值
• （low<high时)保证高位一定等于低位出循环
• 6.此时的数组分为（low右边）大于标准值和（low左边）小于标准值
• 然后分两边递归调用自己
• 7.直到start >= end（low >= high）不会递归下去

具体实现：

static void QuickSort(int[] arr,int start,int end){
    if(start < end){
        int low = start;
        int high = end;
        int standard = arr[low];
        while(low < high){
            while(low < high && standard < arr[high])high--;
            if(low < high)arr[low++] = arr[high];
            while(low < high && standard > arr[low])low++;
            if(low < high)arr[high--] = arr[low];
        }
        arr[low] = standard;
        QuickSort(arr, start, low-1);
        QuickSort(arr, low + 1,end);
    }
}

三、基础版插入排序InsertSort

static void insertSort(int[] arr){
    for(int i = 1;i<arr.length;i++){
    int target = arr[i];
    int j = i-1;
    while(j>-1&&target<arr[j]){
        arr[j+1] = arr[j];
        j--;
    }
    arr[j+1] = target;
}
}

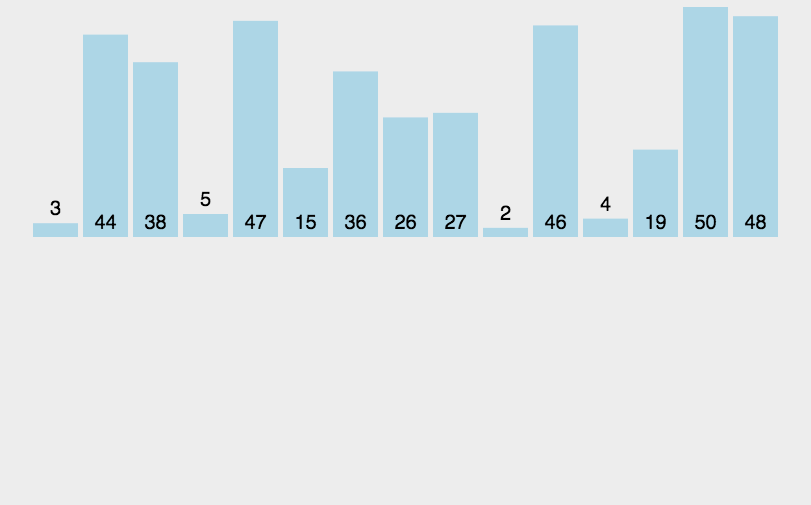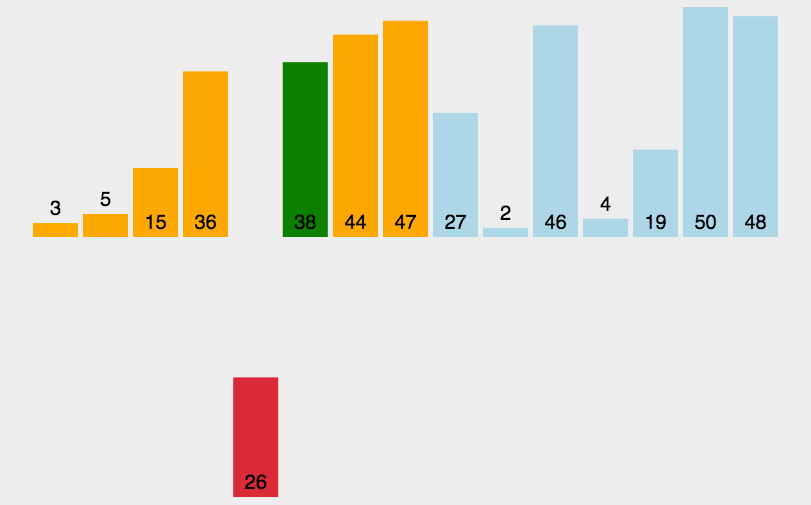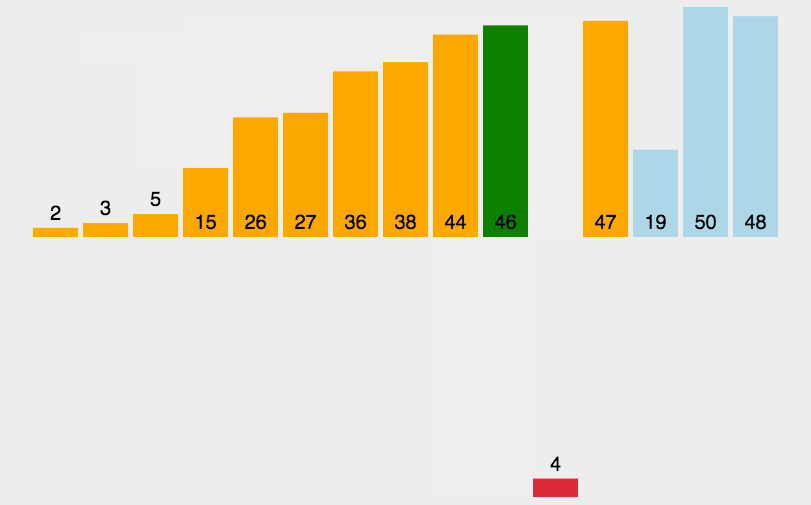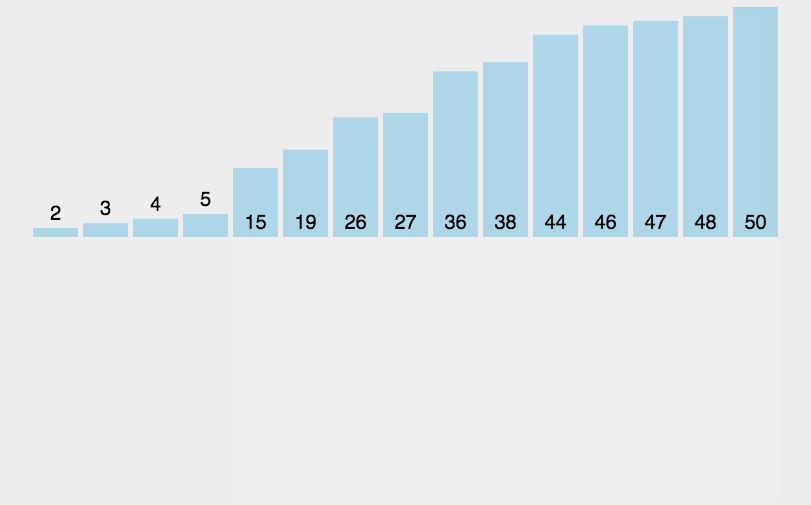
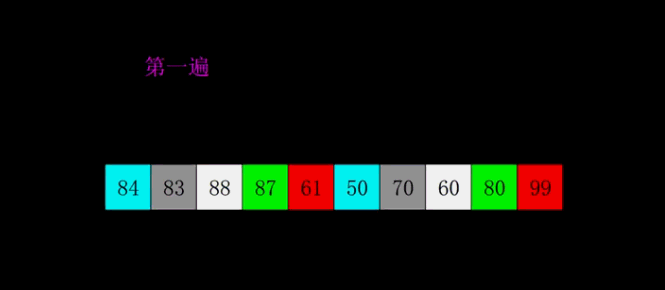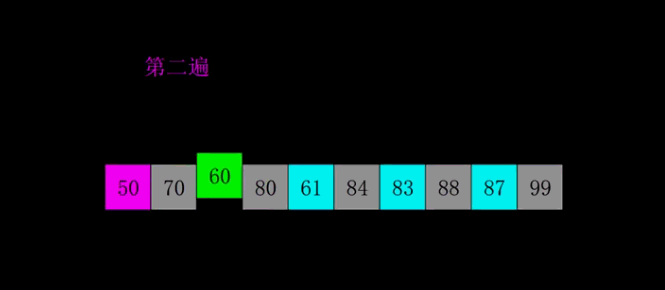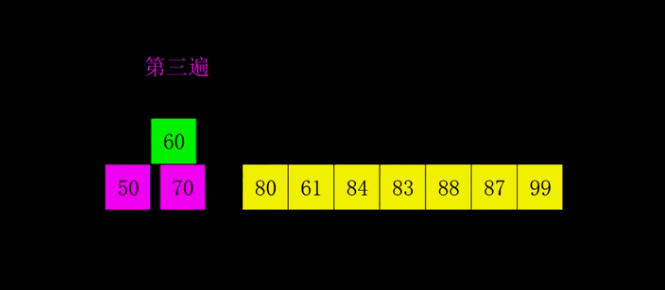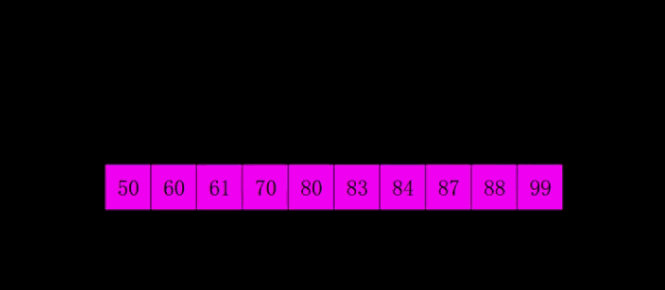
四、希尔排序ShellSort

基本思路：设定一个间隔值，分成一个个小的插入排序

static void ShellSort(int[] arr){
    for(int interval = arr.length/2;interval>0;interval/=2){
    for(int i = interval;i<arr.length;i++){
        int target = arr[i];
        int j = i-interval;
        while(j>-1&&target<arr[j]){
            arr[j+interval] = arr[j];
            j -= interval;
        }
        arr[j+interval] = target;
    }
}
}

五、选择排序SelectSort

static void selectSort(int[] arr){
    int min = 0;
    int count = 0;
    for(int i = 0;i<arr.length;i++){
        min = arr[i];
        count = 0;
        for(int j = i;j<arr.length-1;j++){
            if(min>arr[j+1]){
                min = arr[j+1];
                count = j+1;
                
            }
        }
        if(min == arr[i])continue;
        int temp = arr[count];
        arr[count] = arr[i];
        arr[i] = temp;
    }
}

并查集

#include <bits\stdc++.h>
using namespace std;
int pa[1000005];
int find(int x) {
int x_root = x;
while(x_root != pa[x_root]) {
//在find查询中嵌入一个路径压缩操作
pa[x_root]=pa[pa[x_root]];
//p元素不再选择原来的父亲节点，而是直接选择父亲节点的父亲节点来做为自己新的一个父亲节点
//这样的操作使得树的层数被压缩了
x_root=pa[x_root];//p压缩完毕后且p并不是根节点，p变成p新的父节点继续进行查找和压缩的同时操作
}
return x_root;
}

void merge(int x,int y)//推断x,y是否连通。若不连通。则使其连通。

{
int fx,fy;
fx=find(x);
fy=find(y);
if(fx!=fy)
pa[fx]=fy;
}
set<int> s;
int main() {
for(int i = 0; i < 100000; i++) {
pa[i] = i;
}
int n;
cin >> n;
int zong = 0;
while(n--) {
int t, x;
cin >> t;
cin >> x;
s.insert(x);
for(int i = 0; i < t - 1; i++) {
int k;
cin >> k;
s.insert(k);
merge(x, k);
}
}
int buluo = 0;
for(int i = 1; i <= s.size(); i++) {
if(pa[i] == i) {
buluo++;
}
}
cout << s.size() <<" " << buluo <<endl;
int q;
cin >> q;
while(q--) {
int xx, yy;
cin >> xx >> yy;
if(find(xx) == find(yy)) {
cout << "Y" << endl;
} else {
cout <<"N" <<endl;
}
}

二分查找

import java.util.Arrays;
public class Main{
    static int BinarySearch(int a[],int x, int left, int right) {
        while(left <= right) {
            int mid = (left - right) / 2 + right;
            if(a[mid] < x) {
                left = mid + 1;
            } else if (a[mid] > x) {
                right = mid - 1;
            } else {
                return mid;
            }
        }
        return -1;
    }
    public static void main(String[] args){
        int[] arr = new int[10000];
        for (int i = 0; i < 10000; i++) {
            arr[i] = i;
        }
        System.out.println(BinarySearch(arr,9,1,10));
        System.out.println(Arrays.binarySearch(arr,9));
    }

}

快速幂

public class Main{
    static long fastpow(int a, int b) {
        // 求 a 的 b 次方
        long ans = 1;
        while(b>=1) {
            if((b & 1)>=1) ans *= a;
            a *= a;
            b >>= 1;
        }
        return ans;
    }
    public static void main(String[] args){
        int[] arr = new int[10000];
        for (int i = 0; i < 10000; i++) {
            arr[i] = i;
        }
        System.out.println(fastpow(3,70));
    }

}

全排列

public void Permutation(char chs[],int start )
    {
        if(start==chs.length-1)
        {
            Arrays.toString(chs);
            //如果已经到了数组的最后一个元素，前面的元素已经排好，输出。
        }
        for(int i=start;i<=chs.length-1;i++)
        {
        //把第一个元素分别与后面的元素进行交换，递归的调用其子数组进行排序
                Swap(chs,i,start);
                Permutation(chs,start+1);
                Swap(chs,i,start);
        //子数组排序返回后要将第一个元素交换回来。  
        //如果不交换回来会出错，比如说第一次1、2交换，第一个位置为2，子数组排序返回后如果不将1、2
        //交换回来第二次交换的时候就会将2、3交换，因此必须将1、2交换使1还是在第一个位置 
        }
    }
    public void Swap(char chs[],int i,int j)
    {
        char temp;
        temp=chs[i];
        chs[i]=chs[j];
        chs[j]=temp;
    }

DFS

全排列：

import java.util.Scanner;

public class Main{
    static int n;
    static boolean used[] = new boolean[10];
    static int ans[] = new int[10];
    static void dfs(int u){
        if(u == n+1){
            for (int i = 1; i <=n ; i++) {
                System.out.print(ans[i]);
            }
            System.out.println();
            return;
        }
        for (int i = 1; i <=n; i++) {
            if(!used[i]){
                ans[u] = i;
                used[i] = true;
                dfs(u+1);
                used[i] = false;//回溯
            }
        }
        return;
    }
    public static void main(String[] args){
        Scanner input = new Scanner(System.in);
        n = input.nextInt();
        dfs(1);
    }
}

模板：

void dfs()//参数用来表示状态  
{  
    if(到达终点状态)  
    {  
        ...//根据题意添加  
        return;  
    }  
    if(越界或者是不合法状态)  
        return;  
    if(特殊状态)//剪枝
        return ;
    for(扩展方式)  
    {  
        if(扩展方式所达到状态合法)  
        {  
            修改操作;//根据题意来添加  
            标记；  
            dfs（）；  
            (还原标记)；  
            //是否还原标记根据题意  
            //如果加上（还原标记）就是 回溯法  
        }  
 
    }  
}

n;
}
if(越界或者是不合法状态)
return;
if(特殊状态)//剪枝
return ;
for(扩展方式)
{
if(扩展方式所达到状态合法)
{
修改操作;//根据题意来添加
标记；
dfs（）；
(还原标记)；
//是否还原标记根据题意
//如果加上（还原标记）就是 回溯法
}

}  

}