数据结构-树系列之二叉搜索树（二）

最新推荐文章于 2021-03-25 14:17:03 发布

原创最新推荐文章于 2021-03-25 14:17:03 发布 · 475 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#二叉树 #树 #数据结构 #二叉搜索树

学习之路同时被 2 个专栏收录

24 篇文章

订阅专栏

技术基础

15 篇文章

订阅专栏

本文着重介绍二叉搜索树，包括其定义、性质，还阐述了创建、查找、插入和删除操作。创建时按序列规则构建，查找通过递归，插入需检测元素是否存在，删除分四种情况处理，使用二叉搜索树可提高查找效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

二叉树的基本概念与定义在前文中已经介绍过了，那么此后的几篇文章开始着重于二叉树的实际运用，现在先介绍一篇二叉搜索树，见名知意，此树肯定是用在搜索查找的场景啦。

文章目录

- - 二叉搜索树

二叉搜索树

定义

二叉搜索树又称二叉查找树，亦称为二叉排序树。设x为二叉查找树中的一个节点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个节点，则key[y] <= key[x]；如果y是x的右子树的一个节点，则key[y] >= key[x]。

性质

（1）若左子树不空，则左子树上所有节点的值均小于它的根节点的值；
（2）若右子树不空，则右子树上所有节点的值均大于它的根节点的值；
（3）左、右子树也分别为二叉搜索树；

例如：
图示为一棵二叉搜索树
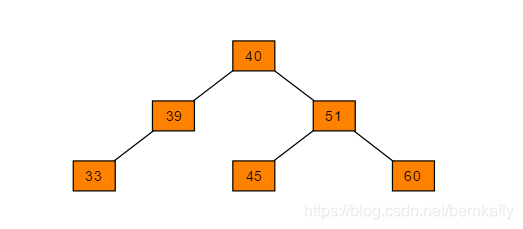
在这里插入图片描述

图示不是一棵二叉搜索树，因为节点40的左孩子节点值为44，不满足二叉搜索树的定义。
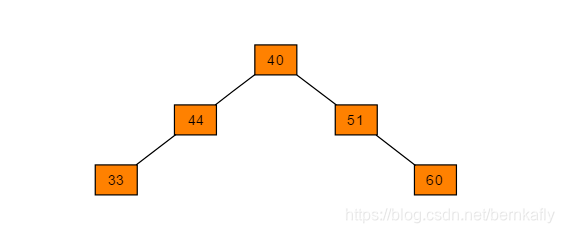
在这里插入图片描述

创建二叉搜索树

现有序列：A = {61, 87, 59, 47, 35, 73, 51, 98, 37, 93}。根据此序列构造二叉搜索树过程如下：

（1）i = 0，A[0] = 61，节点61作为根节点；
（2）i = 1，A[1] = 87，87 > 61，且节点61右孩子为空，故81为61节点的右孩子；
（3）i = 2，A[2] = 59，59 < 61，且节点61左孩子为空，故59为61节点的左孩子；
（4）i = 3，A[3] = 47，47 < 59，且节点59左孩子为空，故47为59节点的左孩子；
（5）i = 4，A[4] = 35，35 < 47，且节点47左孩子为空，故35为47节点的左孩子；
（6）i = 5，A[5] = 73，73 < 87，且节点87左孩子为空，故73为87节点的左孩子；
（7）i = 6，A[6] = 51，47 < 51，且节点47右孩子为空，故51为47节点的右孩子；
（8）i = 7，A[7] = 98，98 < 87，且节点87右孩子为空，故98为87节点的右孩子；
（9）i = 8，A[8] = 93，93 < 98，且节点98左孩子为空，故93为98节点的左孩子；

创建完毕后如图：

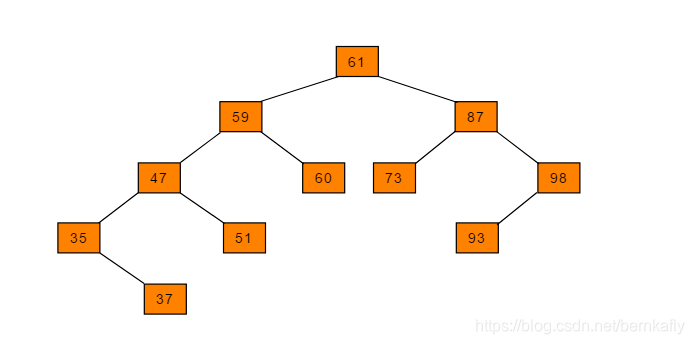
图2.4图2.4

查找

查找过程

（1）如果树是空的，则查找结束，无匹配。
（2）如果被查找的值和节点的值相等，查找成功。
（3）如果被查找的值小于节点的值，递归查找左子树，
（4）如果被查找的值大于节点的值，递归查找右子树，
2.5.2 代码实现

    /* 递归查找二叉排序树T中是否存在key, */
    /* 指针f指向T的双亲，其初始调用值为NULL */
    /* 若查找成功，则指针p指向该数据元素节点，并返回TRUE */
    /* 否则指针p指向查找路径上访问的最后一个节点并返回FALSE */

    bool searchBST(BSTNode* T, int key, BSTNode* f, BSTNode **p)
    {  
        if (!T) /*  查找不成功 */
        { 
            *p = f;  
            return false; 
        }
        else if (key == T->key) /*  查找成功 */
        { 
            *p = T;  
            return true; 
        } 
        else if (key < T->key) 
            return searchBST(T->lchild, key, T, p);  /*  在左子树中继续查找 */
        else  
            return searchBST(T->rchild, key, T, p);  /*  在右子树中继续查找 */
    }

使用二叉搜索树可以提高查找效率，其平均时间复杂度为O(log2n)。
最好的情况为二叉搜索树完全平衡，这样查找可以看作是一个二分查找；
最坏的情况是二叉搜索树为一颗斜树，即根节点为max或者min值，这样最坏情况会遍历整棵树！

插入

插入过程

（1）先检测该元素是否在树中已经存在。如果已经存在，则不进行插入；
（2）若元素不存在，则进行查找过程，并将元素插入在查找结束的位置。

图解过程

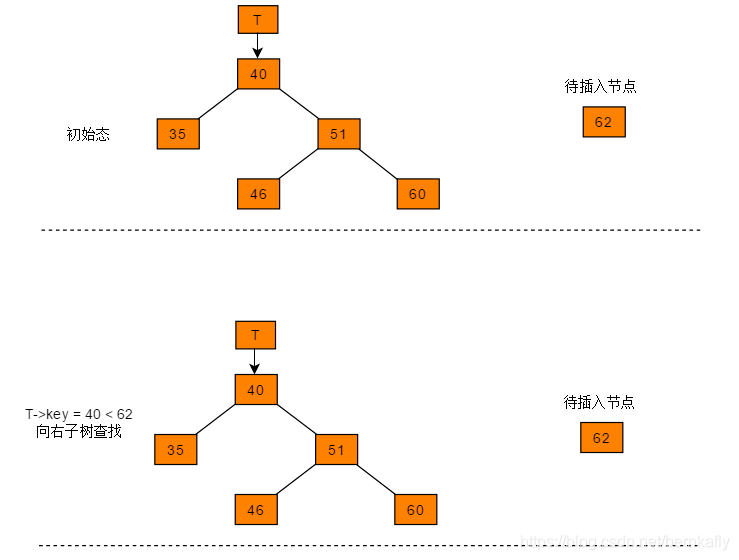
在这里插入图片描述

代码实现

    void insertBST(BSTNode **T,int key) //此处使用二重指针是因为要修改指针的指针
    {
        BSTNode *s;
        if(*T==NULL) //到达查找结束位置，再次位置插入元素
        {
            s = (BSTNode*)malloc(sizeof(BSTNode));
            s->key = key;
            s->lchild = NULL;
            s->rchild = NULL;
            *T=s;
        }
        else if(key<(*T)->key)//要插入的值大于当前节点，往左子树搜
        {
            insertBST(&((*T)->lchild),key);
        }
        else if(key>(*T)->key)//大于当前节点，往右子树搜
        {
            insertBST(&((*T)->rchild),key);
        }
    }

删除

删除的情况比插入要复杂一些，主要分四种情况：
1）删除节点为叶子节点
2）3）删除的节点只有左子树或右子树
4）删除的节点既有左子树又有右子树

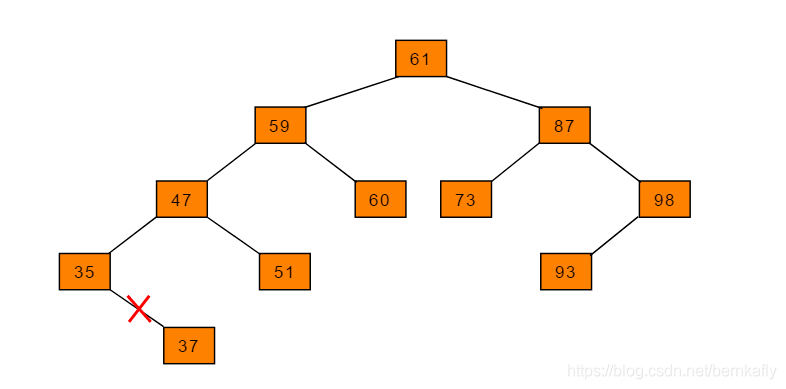
删除节点为叶子节点

删除叶子节点的方式最为简单，只需查找到该节点，直接删除即可。例如删除图2.4中的叶子节点37、节点51、节点60、节点73和节点93的方式是相同的。
在这里插入图片描述

删除的节点只有左子树

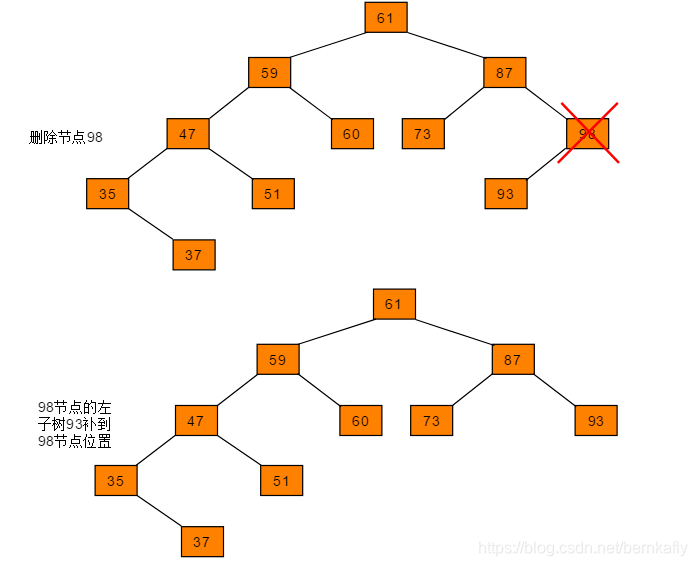
删除的节点若只有左子树，将节点的左子树替代该节点位置。例如删除图中的98节点：
在这里插入图片描述

删除的节点只有右子树

删除的节点若只有右子树，将节点的右子树替代该节点位置。这种情况与删除左子树处理方式类似，不再赘述。

删除的节点既有左子树又有右子树

若删除的节点既有左子树又有右子树，这种节点删除过程相对复杂。其流程如下：
（1）遍历待删除节点的左子树，找到其左子树中的最大节点，即删除节点的前驱节点；
（2）将最大节点代替被删除节点；
（3）删除左子树中的最大节点；
（4）删除最大节点的情况仍然有两种情况（想想看为什么），则递归执行删除。
因为最大节点要么是叶子节点，要么只有左子树，因为要是它有右子树的话，它就不是最大节点了啊。

注：同样可以使用删除节点的右子树中最小节点，即后继节点代替删除节点，此流程与使用前驱节点类似。

也就是说，当我们删除的节点既有左子树又有右子树的情况下，我们有两种删除策略，一种是删除节点，然后把左子树的最大节点置于删除节点所在的位置，一种是删除节点，把右子树的最小节点置于删除节点所在的位置。

代码实现：

    //若二叉排序树T中存在关键字等于key的数据元素时，则删除该数据元素节点
    //并返回TRUE；否则返回FALSE。
    bool deleteBST(BSTNode* T,int key)
    { 
        if(!*T) /* 不存在关键字等于key的数据元素 */ 
            return false;
        else
        {
            if (key == (*T)->key) /* 找到关键字等于key的数据元素 */ 
                return deleteBSTNode(T);
            else if (key<(*T)->key)
                return deleteBST(&(*T)->lchild,key);
            else
                return deleteBST(&(*T)->rchild,key);

        }
    }
    /* 从二叉排序树中删除节点p，并重接它的左或右子树。 */
    bool deleteBSTNode(BSTNode* p)
    {
        BSTNode* q,s;
        if((*p)->rchild==NULL) //右子树空则只需重接它的左子树（待删节点是叶子也走此分支) 
        {
            q=*p;
            *p=(*p)->lchild; 
            free(q);
        }
        else if((*p)->lchild==NULL) //左子树为空，只需重接它的右子树
        {
            q=*p; 
            *p=(*p)->rchild; 
            free(q);
        }
        else //左右子树均不空
        {
            q=*p; 
            s=(*p)->lchild;
            while(s->rchild) // 转到左子树，然后向右到尽头（找待删节点的前驱） */
            {
                q=s;
                s=s->rchild;
            }
            (*p)->key=s->key; //s指向被删节点的直接前驱（将被删节点前驱的值取代被删节点的值）
            if(q!=*p)
                q->rchild=s->lchild; //重接q的右子树
            else
                q->lchild=s->lchild; //重接q的左子树
            free(s);
        }
        return TRUE;
    }

本文部分参考：https://xiaozhuanlan.com/topic/5036471892 同学们可以移步去看一看