【算法题】在一个长度为n的数组里的所有数字都在1到n-1的范围内。 有一个数字重复若干次，找出这个数字。

一般的方法还是见一个字典保存已经出现的数字，然后判断后面的数字是否出现在字典中。
 

def get_dup(lst):
    cnt={}
    for i in lst:
        if i in cnt:
            return i
        else:
            cnt[i]=1

节省空间复杂度的方法，利用保存着1～N-1这个条件。具一个特例，重复的数字出现两次，那么1～N-1都至少出现一次，当这些数字在自己的位置即a[n]=n,此时出现a[0]的数字就是重复的。

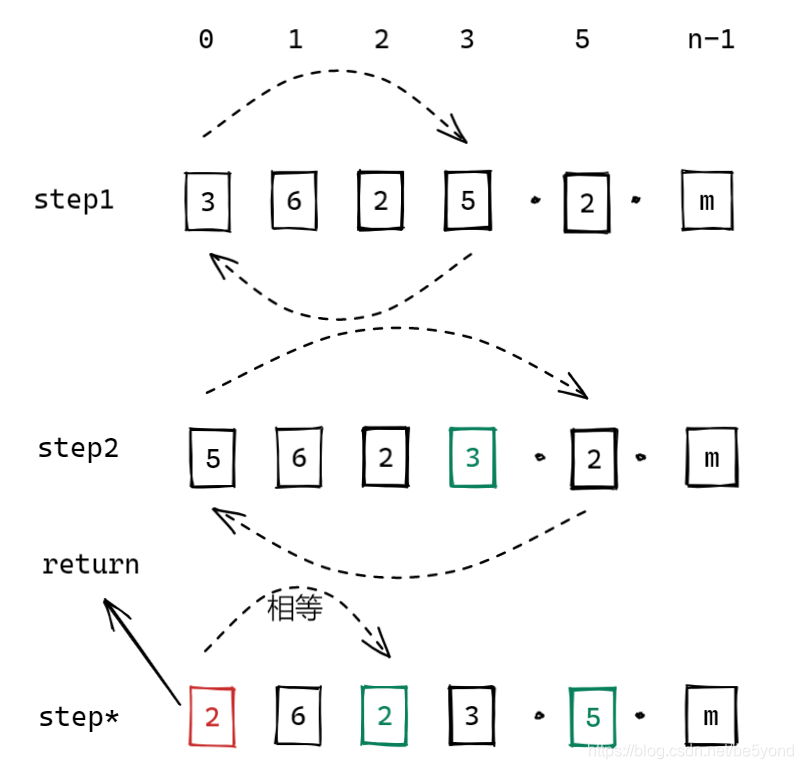
a[0]保存的肯定不是0，

① 假设a[0]=3, a[3]=5, 将a[0]与a[3]交换，a[3]=3

② 现在a[0]=5,  再将a[0]与a[5]交换，a[5]=5

③ a[0] = x, 再将a[0] 与 a[x]交换   a[x] = x

直到交换到, 该位置中的数与我想换进去的数相等则跳出。

代码如下: 

def get_dup(lst):
    key = lst[0]
    while not key==lst[key]:
        key, lst[key] = lst[key], key
    return key