北邮22信通：（7）实验1 题目四：一元多项式（节省内存版）

原创 已于 2023-08-05 23:31:31 修改 · 695 阅读 · 5 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#链表 #数据结构 #算法 #c++

于 2023-03-25 16:43:34 首次发布
本文介绍了北邮22信通学生基于数据结构与算法课程，使用线性表（链表和顺序表）实现一元多项式的输入、输出、加减乘法及求导和求值等功能。文章详细分析了存储结构、关键算法和代码实现，特别讨论了节省内存的优化策略。并提供了C++代码示例和程序运行结果。

北邮22信通一枚~   

跟随课程进度每周更新数据结构与算法的代码和文章 

持续关注作者  解锁更多邮苑信通专属代码~

获取更多文章  请访问专栏：

北邮22信通_青山如墨雨如画的博客-优快云博客

目录

1.实验要求：

2.程序分析：

2.1存储结构

2.2关键算法分析

2.2.1关键算法：

2.2.2代码详细分析：

3.完整代码

  4.程序运行结果：

1.实验要求：

 利用线性表实现一个一元多项式，可以用链表实现，也可以用顺序表实现。

要求：

能够实现一元多项式的输入和输出

能够实现一元多项式的相加；

能够实现一元多项式的相减；

能够计算一元多项式在x处的值；

能够计算一元多项式的导数；

能够进行一元多项式的相乘；

编写测试main（）函数测试线性表的正确性；

2.程序分析：

***声明***

1.为什么有节省内存与否的区分：

        有些友友这样处理问题：链表按顺序依次为x的0次方，x的1次方，x的2次方……这样写不是更加方便简单吗？

        这样写起来确实会方便很多，但是有没有考虑过一个问题：如果我要实现x^10000+1和x^1000000+1相乘，不仅储存起来会非常占内存，而且程序运行时间也很长！

        面向几个多项式的加减乘法，似乎没有什么区别，但是如果应用于工程实践，这个方法可能就不是最优解了，所以，本代码实现的是“节省内存版”，使用这个代码，让你最大程度利用内存空间！

2.一点选择：

        由于操作方便性的问题，本代码将数据类型定义为类，并在类中实现了一些函数方法，便于书写模板类时直接调用。

        同时，由于虚拟函数类型写成了类，因为操作数个数的要求，有些函数必须声明为友元函数，所以本代码中友元函数众多。如果将虚拟数据类型定义为结构体，那么直接使用普通的成员函数就可以实现功能，不需要友元函数。所以还是上面那个问题，要想实现模板类的时候简单点，就将虚拟数据类型定义为类，缺点是友元函数太多；如果不太想写这么多友元函数，那就将虚拟数据类型定义为结构体，缺点是书写模板类函数成员的时候会麻烦一些。

***声明完毕***

2.1存储结构

单链表 虚拟数据类型：类

2.2关键算法分析

2.2.1关键算法：

按顺序插入函数，求导函数，求值函数，实现多项式乘法的函数，实现多项式加减法的函数。

2.2.2代码详细分析：

        2.2.2.1insert函数：重点函数！！！（后面所有的函数几乎都用上了它！！！）

                定义指向链表首结点的指针p

                首先对结果链表的情况分类：链表中有数据、链表中没有数据。

                如果链表中没有数据，那么新建立结点，直接将结点插入到链表中；

                如果链表中有数据：

                建立新结点，传入数据；

                遍历链表；

        如果遍历到某个结点，这个节点的数据域中的指数小于新建结点数据域中的指数，并且该结点的下一个节点的数据域中的指数小于新建结点数据中的指数，那么指针p向后移动一位；

        如果遍历到某个结点，这个节点的数据域中的指数小于新建结点数据域中的指数，并且该结点的下一个结点的数据域中的指数大于新建结点数据域中的指数，那么将新建结点插入到这个位置，停止遍历；

        如果遍历到某个结点，这个节点的数据域中的指数等于新建结点数据域中的指数，那么调用单项式相加的函数，将两个结点的数据域相加，停止遍历；

        如果指针p循环到最后还没有执行break语句，那说明新建结点数据域中的指数大于该链表中任一结点数据域中的指数，直接插入到尾部即可；

template<class temp>
void linklist<temp>::insert(temp x)
{
	int flag = 0;
	node<temp>* p = this->front->next;
	if (p == NULL)
	{
		node<temp>* s = new node<temp>;
		s->data = x;
		s->next = NULL;
		p = s;
	}
	while (p->next != NULL)
	{
		if (p->data.getzhishu() < x.getzhishu() &&
			p->next->data.getzhishu() < x.getzhishu())
			p = p->next;
		else if (p->data.getzhishu() < x.getzhishu() &&
			p->next->data.getzhishu() > x.getzhishu())
		{
			node<temp>* s = new node<temp>;
			s->data = x;
			s->next = p->next;
			p->next = s;
			flag = 1;
			break;
		}
		else if (p->data.getzhishu() < x.getzhishu() &&
			p->next->data.getzhishu() == x.getzhishu())
		{
			p->next->data = p->next->data + x;
			flag = 1;
			break;
		}
	}
	if (flag == 0)
	{
		node<temp>* s = new node<temp>;
		s->data = x;
		s->next = NULL;
		p->next = s;
	}
}

        2.2.2.2求导函数：

                   时间复杂度O(n)

                先在存储数据的类中定义友元函数形式的单项式求导函数：

                如果指数为0，那么返回的对象的指数和系数都为0；

                如果指数不为0并且系数也不为0，那么返回的对象中，

                系数变为原对象系数和指数的乘积，返回对象的系数执行自减；

                在模板类中，定义指向链表首结点的指针；

                遍历链表，对每个节点的数据域，调用上文提到的友元函数形式的单项式求导函数；

//虚拟数据类型中定义的单项式求导
friend danxiangshi danxiangshiqiudao(danxiangshi& a)
	{
		if (a.zhishu == 0)
		{
			a.xishu = 0;
			a.zhishu = 0;
		}
		else if (a.xishu != 0 && a.zhishu != 0)
		{
			a.xishu = a.xishu * a.zhishu;
			a.zhishu--;
		}
		return a;
	}
//模板类中定义的多项式求导
template<class temp>
inline void linklist<temp>::qiudao()
{
	cout << "求导后的结果为:" << endl;
	node<temp>* p = this->front->next;
	while (p != NULL)
	{
		p->data = danxiangshiqiudao(p->data);
		p = p->next;
	}

}

        2.2.2.3求值函数：

                   时间复杂度O(n)

                方法与上面的求导函数的方法相似，这里不做赘述；

        2.2.2.4多项式加法函数：

                   时间复杂度O(n)

                在模板类中定义友元函数形式的多项式加法函数；

                调用2.2.2.1的插入函数，依次将每个链表的每个结点插入到结果链表中，即可实现；

	friend void duoxiangshijiafa(linklist<temp>& list0, linklist<temp>& list1, linklist<temp>& list2)
	{
		node<temp>* p = list1.front->next;
		node<temp>* q = list2.front->next;
		while (p != NULL)
		{
			list0.insert(p->data);
			p = p->next;
		}
		while (q != NULL)
		{
			list0.insert(q->data);
			q = q->next;
		}
	}

        2.2.2.5多项式减法函数：        

                时间复杂度O(n)

                在模板类中定义友元函数形式的多项式减法函数；

                多项式减法函数与上面的多项式加法函数实现方法类似，唯一不同的是，

                减法相当于加上负的，这个过程需要通过至少一个函数来完成，

                这些个函数共同完成的事情只有一件：

                将减数的所有项变成相反数；

                在虚拟数据类型中定义turntoxiangfanshu函数，将系数变成相反数吗，指数不变；

                在模板类实现减法的过程中，遍历减数多项式的时候，

                对每一个数据域，都将数据域传入到这个turntoxiangfanshu函数中做一次变换，

                再调用多项式加法相似的方法，就解决了问题；

                所以这里有两种思路：

                1.单独遍历减数多项式链表，对每个数据域做变换，

                之后调用insert函数将减数被减数插入到结果多项式链表中；

                2.单独遍历减数多项式链表，对每个数据域做变换，

                之后直接调用多项式相加函数，返回值；

                本代码采用的是第一种思路；

	friend void duoxiangshijianfa(linklist<temp>& list0, linklist<temp>& list1, linklist<temp>& list2)
	{
		node<temp>* p = list1.front->next;
		node<temp>* q = list2.front->next;
		while (p != NULL)
		{
			list0.insert(p->data);
			p = p->next;
		}
		while (q != NULL)
		{
			list0.insert(turntoxiangfanshu(q->data));
			turntoxiangfanshu(q->data);
			q = q->next;
		}
	}

        2.2.2.6多项式乘法函数：

                时间复杂度O(n^2)

                在模板类中定义友元函数形式的多形式乘法函数；

                在数据域的类中重载乘法运算符号，在多项式乘法函数中：

                定义指向参与运算的链表1首结点的指针p1；

                定义指针p2；

                依次取链表1中的一个结点，对每次取到一个结点：

                让p2重新指向链表2的首结点；

                遍历链表2，对链表2的每个结点，分别与链表1中取到的结点相乘，

                并将结果插入到结果链表中；

                链表1取下一个结点；

	friend void duoxiangshichengfa(linklist<temp>& list0, linklist<temp>& list1, linklist<temp>& list2)
	{
		node<temp>* p = list1.front->next;
		node<temp>* q = NULL;
		while (p != NULL)
		{
			q = list2.front->next;
			while (q != NULL)
			{
				list0.insert(p->data * q->data);
				q = q->next;
			}
			p = p->next;
		}
	}

3.完整代码

#include<iostream>
#include <iomanip>
#include <cmath>

using namespace std;

class danxiangshi
{
private:
	double xishu;
	int zhishu;
public:
	danxiangshi()
	{
		this->xishu = 0;
		this->zhishu = 0;
	}
	danxiangshi(double, int);
	void getinfo(double, int);
	int getzhishu();
	double getxishu();

	void print();

	//friend void operator = (danxiangshi&,danxiangshi&);
	danxiangshi operator+(danxiangshi&);
	danxiangshi operator *(danxiangshi&);

	friend danxiangshi turntoxiangfanshu(danxiangshi& a)
	{
		a.xishu = -a.xishu;
		a.zhishu = a.zhishu;
		return a;
	}

	friend double danxiangshiqiuzhi(double x, danxiangshi& a)
	{
		return a.xishu * pow(x * 1.0, a.zhishu);
	}

	friend danxiangshi danxiangshiqiudao(danxiangshi& a)
	{
		if (a.zhishu == 0)
		{
			a.xishu = 0;
			a.zhishu = 0;
		}
		else if (a.xishu != 0 && a.zhishu != 0)
		{
			a.xishu = a.xishu * a.zhishu;
			a.zhishu--;
		}
		return a;
	}
};

danxiangshi::danxiangshi(double xishu, int zhishu)
{
	this->xishu = xishu;
	this->zhishu = zhishu;
}

inline void danxiangshi::getinfo(double xishu, int zhishu)
{
	this->xishu = xishu;
	this->zhishu = zhishu;
}

inline int danxiangshi::getzhishu()
{
	return this->zhishu;
}

inline double danxiangshi::getxishu()
{
	return this->xishu;
}

inline void danxiangshi::print()
{
	if (this->xishu == 0)
		return;
	else if (this->xishu != 0 && this->zhishu == 0)
		cout << showpos << this->xishu;
	else if (this->xishu != 0 && this->zhishu != 0)
		cout << showpos << this->xishu << "x^" << noshowpos << this->zhishu;
}

inline danxiangshi danxiangshi::operator+(danxiangshi& a)
{
	danxiangshi c;
	c.xishu += (this->xishu + a.xishu);
	c.zhishu = this->zhishu;
	return c;
}

inline danxiangshi danxiangshi::operator*(danxiangshi& a)
{
	danxiangshi c;
	c.xishu = this->xishu * a.xishu;
	c.zhishu = this->zhishu + a.zhishu;
	return c;
}

template<class temp>
struct node
{
	temp data;
	node<temp>* next;
};

template<class temp>
class linklist
{
private:
	node<temp>* front;
public:
	linklist()
	{
		this->front = new node<temp>;
		this->front->next = NULL;
	}
	linklist(temp a[], int x);
	~linklist();
	node<temp>* get(int i);
	void insert(temp x);
	void printlist();
	void qiudao();
	void qiuzhi(double x);

	friend void duoxiangshichengfa(linklist<temp>& list0, 
		linklist<temp>& list1, linklist<temp>& list2)
	{
		node<temp>* p = list1.front->next;
		node<temp>* q = NULL;
		while (p != NULL)
		{
			q = list2.front->next;
			while (q != NULL)
			{
				list0.insert(p->data * q->data);
				q = q->next;
			}
			p = p->next;
		}
	}

	friend void duoxiangshijiafa(linklist<temp>& list0, 
		linklist<temp>& list1, linklist<temp>& list2)
	{
		node<temp>* p = list1.front->next;
		node<temp>* q = list2.front->next;
		while (p != NULL)
		{
			list0.insert(p->data);
			p = p->next;
		}
		while (q != NULL)
		{
			list0.insert(q->data);
			q = q->next;
		}
	}

	friend void duoxiangshijianfa(linklist<temp>& list0, 
		linklist<temp>& list1, linklist<temp>& list2)
	{
		node<temp>* p = list1.front->next;
		node<temp>* q = list2.front->next;
		while (p != NULL)
		{
			list0.insert(p->data);
			p = p->next;
		}
		while (q != NULL)
		{
			list0.insert(turntoxiangfanshu(q->data));
			turntoxiangfanshu(q->data);
			q = q->next;
		}
	}

};

template<class temp>
linklist<temp>::linklist(temp a[], int n)
{
	this->front = new node<temp>;
	this->front->next = NULL;
	for (int i = n - 1; i >= 0; i--)
	{
		node<temp>* s = new node<temp>;
		s->data = a[i];
		s->next = this->front->next;
		this->front->next = s;
	}
}

template<class temp>
linklist<temp>:: ~linklist()
{
	node<temp>* p = this->front;
	while (p != NULL)
	{
		this->front = p;
		p = p->next;
		delete this->front;
	}
}

template<class temp>
node<temp>* linklist<temp>::get(int i)
{
	node<temp>* p = this->front->next;
	int j = 1;
	while (p != NULL && j != i)
	{
		p = p->next;
		j++;
	}
	return p;
}

template<class temp>
void linklist<temp>::insert(temp x)
{
	int flag = 0;
	node<temp>* p = this->front->next;
	if (p == NULL)
	{
		node<temp>* s = new node<temp>;
		s->data = x;
		s->next = NULL;
		p = s;
	}
	while (p->next != NULL)
	{
		if (p->data.getzhishu() < x.getzhishu() &&
			p->next->data.getzhishu() < x.getzhishu())
			p = p->next;
		else if (p->data.getzhishu() < x.getzhishu() &&
			p->next->data.getzhishu() > x.getzhishu())
		{
			node<temp>* s = new node<temp>;
			s->data = x;
			s->next = p->next;
			p->next = s;
			flag = 1;
			break;
		}
		else if (p->data.getzhishu() < x.getzhishu() &&
			p->next->data.getzhishu() == x.getzhishu())
		{
			p->next->data = p->next->data + x;
			flag = 1;
			break;
		}
	}
	if (flag == 0)
	{
		node<temp>* s = new node<temp>;
		s->data = x;
		s->next = NULL;
		p->next = s;
	}
}

template<class temp>
inline void linklist<temp>::printlist()
{
	node<temp>* p = this->front->next;
	while (p != NULL)
	{
		p->data.print();
		p = p->next;
	}
	cout << endl;
	return;
}

template<class temp>
inline void linklist<temp>::qiudao()
{
	cout << "求导后的结果为:" << endl;
	node<temp>* p = this->front->next;
	while (p != NULL)
	{
		p->data = danxiangshiqiudao(p->data);
		p = p->next;
	}

}

template<class temp>
inline void linklist<temp>::qiuzhi(double x)
{
	node<temp>* p = this->front->next;
	double sum = 0;
	while (p != NULL)
	{
		sum += danxiangshiqiuzhi(x, p->data);
		p = p->next;
	}
	cout << "带入x=" << x << "后，多项式的值为：" << sum << endl;
}

int main()
{
	system("color 0A");
	//测试同指数单项式相加函数是否书写正确
	//danxiangshi a(5, 5);
	//danxiangshi b(4, 5);
	//a.operateplus(b);
	//a.print();

	//测试insert函数是否正确
	//danxiangshi x[5] =
	//{
	//	{1,1},{2,2},{3,3},{4,4},{5,5}
	//};
	//danxiangshi record(4,4);
	//linklist<danxiangshi>list(x, 5);
	//list.insert(record);
	//list.printlist();

	//检测求值和求导函数
	danxiangshi x[3] = { {1,1},{2,2},{3,3} };
	danxiangshi y[2] = { {1,1},{2,2} };
	danxiangshi z[100];
	linklist<danxiangshi>list1(x, 3);
	linklist<danxiangshi>list2(y, 2);

	cout << "1.测试多项式加法函数:" << endl;
	linklist<danxiangshi>lista(z, 100);
	duoxiangshijiafa(lista, list1, list2);
	cout << "lista:";
	lista.printlist();

	cout << endl << "2.测试多项式减法函数:" << endl;
	linklist<danxiangshi>listb(z, 100);
	duoxiangshijianfa(listb, list1, list2);
	cout << "listb:";
	listb.printlist();


	cout << endl << "3.测试多项式乘法函数:" << endl;
	linklist<danxiangshi>listc(z, 100);
	duoxiangshichengfa(listc, list1, list2);
	list1.printlist();
	list2.printlist();
	cout << "listc:";
	listc.printlist();

	cout << endl << "4.测试多项式求值函数:" << endl;
	lista.printlist();
	lista.qiuzhi(2);

	cout << endl << "5.测试多项式求导函数:" << endl;
	cout << "以对listc:";
	listc.printlist();
	cout << "求导为例;";
	listc.qiudao();
	listc.printlist();
	return 0;
}

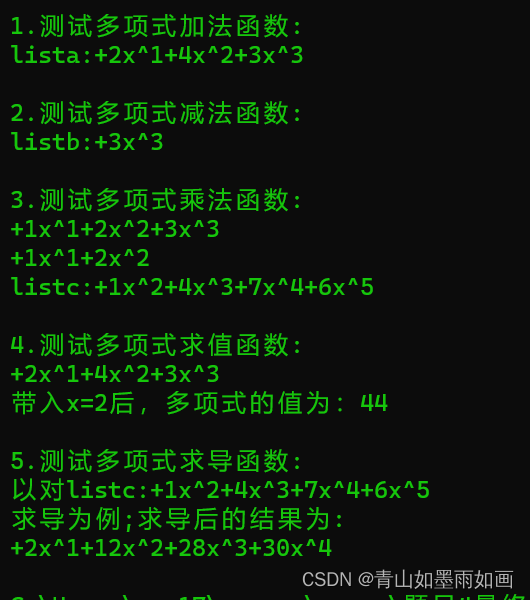
  4.程序运行结果：

代码效果图：

程序运行结果：

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

青山入墨雨如画

你的鼓励将是我创作的动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值