找出一个二维数组中的鞍点与写出一个五阶魔方阵

鞍点：

鞍点就是该元素在这个二维数组中，是它所在行的最大值，并且是它所在列的最小值。
所以找鞍点可以转化为找极值问题。
代码：

int main()
{
	int a[3][3] = {
		10,11,12,
		9,8,7,
		15,14,20};
	int i=0,j = 0,k=0;
		int len1 = sizeof(a) / sizeof(a[0]);
		int len2 = sizeof(a[0]) / sizeof(a[0][0]);
		int max,xb,flag ;
		for (i = 0; i < len1; i++)
		{
			flag = 0;
			max = a[i][0];
			xb = 0;
			for (j = 0; j < len2; j++)
			{
				if (max < a[i][j])
				{
					max = a[i][j];
					xb = j;
				}
			}
			for (k = 0; k < len1; k++)
			{
				if (a[k][xb] < max) {  flag = 1; }
			}
			if (flag == 0) { printf("%d是鞍点", max); break; }
		
		}
		if(i>=len1)printf("没有鞍点");
	
	return 0;
}

主要思想是，先从行遍历，找出这行的最大值，然后确定该值的列下标，然后列下标不变，对每一行进行遍历，如果有小于该数的数，则它就不是鞍点，如果没有就是鞍点。
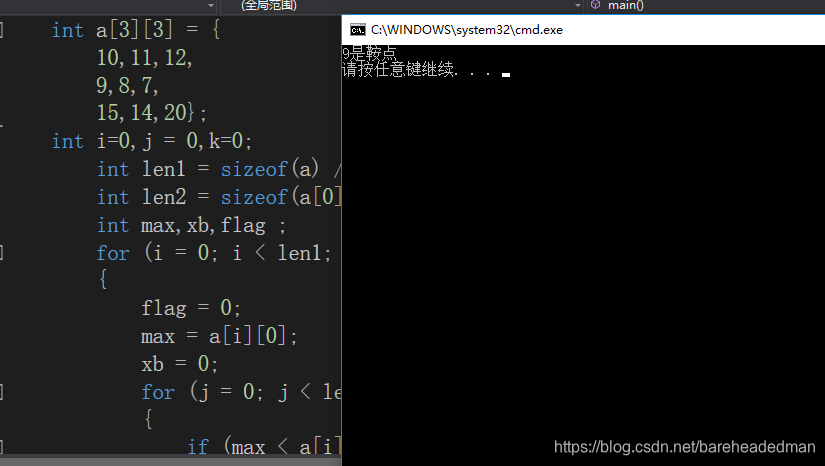
我给定的二维数组的鞍点是9。如图所示：

五阶魔方阵

代码：

int main()
{
	const int n = 5;
	int a[5][5] = { 0 };
	int i = 0;
	int j = n / 2;
	int i1, j1;
	for (int k = 1; k <= n*n; k++)
	{
		a[i][j] = k;
		i1 = i-1;
		j1 = j+1;
		if (i - 1 < 0) { i1 += n; }
		if (j + 1 >= n) { j1 -= n; }
		if (a[i1][j1] != 0)
		{
			i1 = i + 1;
			j1 = j;
		}
		i = i1;
		j = j1;
	}
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			printf("%-3d ",a[i][j]);
		}
		puts("");
	}

	return 0;
}

思想是从第一行的最中间开始，给第一行最中间的位置赋1，给其右上方的位置赋2，如果下标越界了分两种情况，（1）i-1越界，则令i=i-1+n(n为魔方阶数)；（2）j+1越界，则令j=j+1-n；如果下标并没有越界，而是其右上角的位置被占了，那么下一个数就放在上一个数的下方，这样就可以把25个位置全部放满。
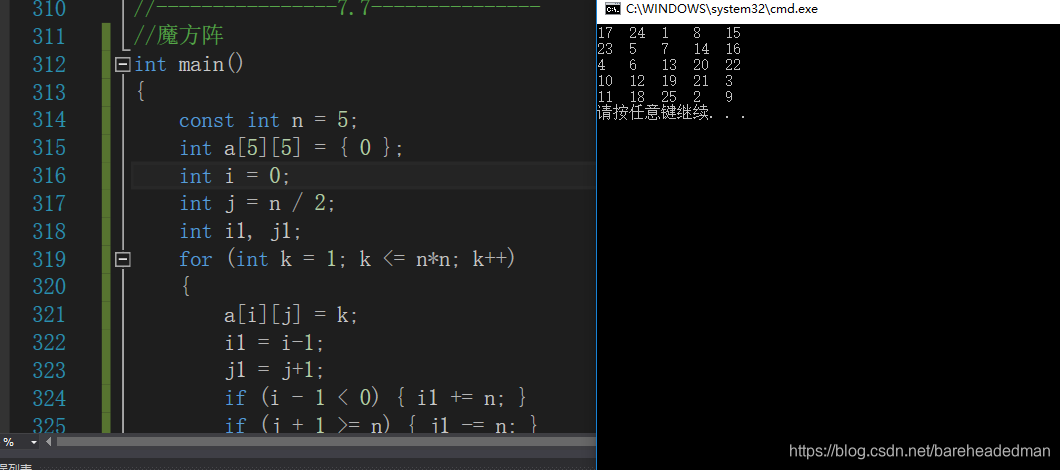
结果如图所示：