华为OD机考2025C卷 - 最大相连男生数 / 学生方阵 （Java & Python& JS & C++ & C ）

最新华为上机考试

真题目录：点击查看目录
华为OD面试真题精选：点击立即查看
2025华为od机试2025C卷-华为OD上机考试2025年C卷

题目描述

学校组织活动，将学生排成一个矩形方阵。

请在矩形方阵中找到最大的位置相连的男生数量。

这个相连位置在一个直线上，方向可以是水平的，垂直的，成对角线的或者呈反对角线的。

注：学生个数不会超过10000

输入描述

输入的第一行为矩阵的行数和列数，接下来的n行为矩阵元素，元素间用”,”分隔。

输出描述

输出一个整数，表示矩阵中最长的位置相连的男生个数。

示例1

输入

3,4
F,M,M,F
F,M,M,F
F,F,F,M

输出

3

说明

解题思路

题目要求在一个由学生组成的矩形方阵中，找到最大的位置相连的男生数量。这里“相连”是指男生的所在位置可以通过水平、垂直、对角线或反对角线方向连续连接。

代码思路

• 遍历整个方阵中的每个元素，当找到一个男生M时，调用getMaxConnected方法，开始从该位置搜索最长连续的M数量。
• getMaxConnected方法实现了四个方向的搜索（水平、垂直、对角线、反对角线）：
  • 水平（从左往右）：从当前位置向右方向扫描，计算连续的M数量。
  • 垂直（从上往下）：从当前位置向下方向扫描，计算连续的M数量。
  • 对角线（左上到右下）：从当前位置向右下方向扫描，计算连续的M数量。
  • 反对角线（右上到左下）：从当前位置向左下方向扫描，计算连续的M数量。
• 每找到一条连续的男生M，将其数量添加到结果列表res中。

示例解释

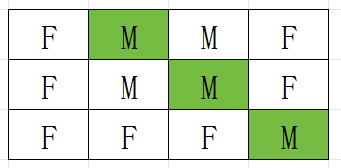
给定输入：

3,4
F,M,M,F
F,M,M,F
F,F,F,M

1. 构建的矩阵为：

   F M M F
   F M M F
   F F F M
   

2. 逐个扫描矩阵，当扫描到M时（如[0,1]位置的M），开始四个方向的搜索。

   • 水平：M (0,1) 和 (0,2)，长度为2
   • 垂直：M (0,1), (1,1)，长度为2
   • 对角线：M (0,1)，只有一个
   • 反对角线：M (0,2), (1,3)，长度为2

3. 将结果存入max_res，最后在整个矩阵中找到的最大连续M<