前段时间由于各种各样的事情太忙,优快云博客停止有很长一段时间了。今天为大家分享一个JAVA窗体版本的最短路径算法动态演示系统474.目前基于Swing的窗体程序使用越来越少。但是通过窗体程序涉及到的技术在各种应用程序中都有广泛的应用。本次介绍最短路径算法动态演示系统还是做的非常好,项目涉及到I/O技术、UI技术、多线程技术等,是一个实战性很强的项目。项目的主要功能包括:设置节点位置、边线权重、动态显示Dijkstra算法运行步骤和结果、导出JSON、查看使用帮助等功能。通过本系统可以非常清晰的了解Dijkstra的运算过程,对于理解算法和后续的进一步学习有非常大的帮助。整个项目有完整得源码,希望大家可以喜欢。通过实战项目,喜欢上编程,提高编程水平,一起加油!
项目背景和目的
Dijkstra算法是一种用于在图中找到单个源点到所有其他顶点的最短路径的算法。该算法由荷兰计算机科学家Edsger Dijkstra在1956年提出。它特别适用于带有非负权重的有向图或无向图。Dijkstra算法不能用于包含负权边的图,因为在这种情况下它可能无法正确工作。
Dijkstra算法的基本思想是,从源点开始,逐步向外探索,更新到达图中各个顶点的最短路径。算法维护一个距离数组dist[],其中dist[i]表示从源点到顶点i的当前已知最短距离。算法还维护一个集合S,其中包含已经找到最短路径的顶点。
算法步骤
-
初始化:将所有顶点的距离设为无穷大(除了源点,其距离设为0)。将源点加入集合
S。 -
寻找最近顶点:在未处理的顶点中找出距离最小的顶点
u(即dist[u]的值最小),并将u添加到集合S中。 -
更新距离:对于每个与
u相邻的顶点v,如果通过u到达v的距离比已知的更短(即dist[u] + weight(u, v) < dist[v]),则更新dist[v]为dist[u] + weight(u, v)。 -
重复:重复步骤2和3,直到所有顶点都被添加到集合
S中。
理解难点
理解上的难点,特别是对于初学者来说。以下是一些可能导致理解困难的关键点:
-
贪心选择的正确性:
Dijkstra算法的核心是贪心策略,即每一步都选择当前已知距离最小的顶点进行扩展。然而,这种贪心选择的正确性并不是直观的。学生可能会问:“为什么选择当前距离最小的顶点就能保证找到最短路径?”这种正确性需要通过数学归纳法或反证法来证明,但证明过程可能较为复杂,不易直接理解。 -
更新距离的时机:
在算法中,每当一个顶点被加入已处理集合(通常称为“最短路径树”或“集合S”)时,它的所有邻接顶点的距离都可能需要被更新。然而,更新的时机和条件(即只有当通过新加入的顶点能够找到更短的路径时才进行更新)是容易混淆的。学生需要理解这种条件更新是如何保证算法正确性的。 -
优先队列(最小堆)的使用:
为了提高算法效率,特别是在边数较多的稀疏图中,通常使用优先队列(特别是最小堆)来存储和更新顶点的距离。然而,优先队列的使用增加了算法的复杂度,因为它需要维护一个动态的数据结构。学生需要理解如何在每次更新距离时维护优先队列的正确性,以及如何从中高效地选择距离最小的顶点。 -
处理负权边的限制:
Dijkstra算法不能处理包含负权边的图,因为负权边可能破坏算法的贪心选择策略。然而,这种限制的原因和后果可能不是立即显而易见的。学生需要理解为什么负权边会导致算法失效,并了解其他能够处理负权边的算法(如Bellman-Ford算法)。 -
算法的适用范围:
Dijkstra算法适用于带有非负权重的有向图和无向图。然而,学生可能不清楚这种限制如何影响算法的选择和应用。他们需要理解在特定问题中如何选择最合适的算法,并了解算法的局限性。 -
实现细节:
虽然Dijkstra算法的基本思想相对简单,但实现起来却可能包含许多细节问题。例如,如何高效地处理重边和自环?如何避免重复加入已处理集合的顶点?如何处理图中不存在的边?这些细节问题可能会增加实现难度,并导致错误和性能问题。
系统功能架构
系统的功能结构入下图所示,其功能结构入下图所示:
运行效果
1 主界面
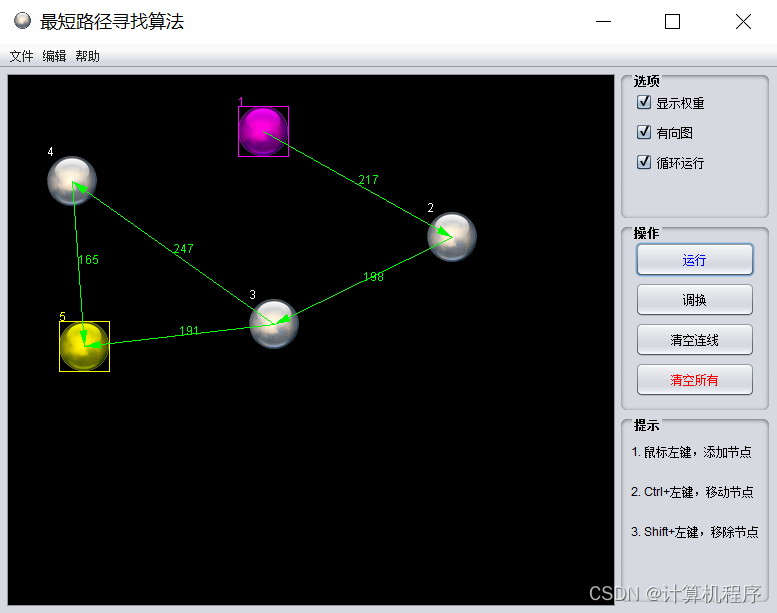
2 导出JSON文件
3 设置背景
4 导入json文件
暂不截图
5 使用帮助

项目总结
(1)在写代码之前,在大脑里一定要把思路理清楚,不能模模糊糊,一定要把功能图和流程图画出来,然后根据它去实现每一个功能块,要多分析,培养一种良好的逻辑思维能力。
(2)在写代码的过程中,一定要采取就近原则,同一个功能,或者对同一个组件的设置一般要写在一块,这样写的程序比较清晰,不容易出错,也便于查找。
(3)要养成良好的注释习惯,一是有利于别人阅读你的程序,同时也有利于自己以后再看,就能很快的读懂程序,提高效率。
(4)把功能模块化,即把实现相同功能的代码段封装成一到一个类或者一个方法中,实现的时候调用即可,这样能提高代码的可读性。





















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










