数据结构学习之:平衡二叉树
一、 平衡二叉树概述
平衡二叉树(AVL树)按个人理解其实是对二叉排序树的一个升级,它其实是解决二叉排序树的一个缺陷,那么二叉排序树存在怎样的缺陷?我们知道二叉排序的查找效率是相对比较高的,不过对于下图这种二叉排序树,它的查找效率并不会提升。

平衡二叉树的出现就是为了解决这种缺陷问题,对我们的二叉树做一个平衡,以便保证它的查询效率,那怎样才能算是一棵平衡二叉树呢?我们这样规定:对于任何一个二叉排序树的非叶子节点,它的左子树和右子树的高度差绝对值不超过1,我们称这中二叉排序树为平衡二叉树。将二叉排序树转换称平衡二叉树有单旋转和双旋转两种方式,接下来我们来介绍这两种转平衡二叉树的方式。
二、平衡二叉树单旋转
1、右旋转
我们看下图的二叉排序树结构:
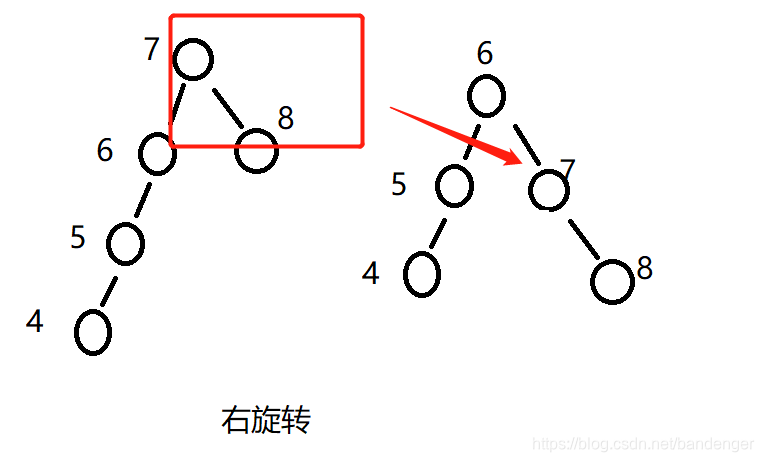
我们看到左侧的二叉排序树中,权值为6的这棵二叉排序树不平衡,因为它的左子树高度为2,右子树高度为0。如果是二叉排序树的左子树高度比右侧大,那么我们以这颗树的不平衡点(图中是权值为6的点)进行顺时针旋转(右旋转),以保持树的平衡。
2、右旋转
同样,如下图所示,权值为6的这棵二叉排序树不平衡,因为它的右子树高度为2,左子树高度为0。如果是二叉排序树的右子树高度比左侧大,那么我们以这颗树的不平衡点(图中是权值为6的点)进行逆时针旋转(左旋转),以保持树的平衡。

三、平衡二叉树双旋转
但是有这样一种情况,如下图所示,这棵不平衡二叉树,单单只进行一次旋转还是达不到平衡的状态,需要进行两次旋转才能达到平衡状态,我们称这种旋转方式为双旋转。

四、代码实现平衡二叉树的单、双旋转
package balancetree;
/**
* 二叉排序树
*/
public class SortNode {
private int value;
private SortNode leftNode;
private SortNode rightNode;
public void setValue(int value) {
this.value = value;
}
public int getValue() {
return value;
}
public SortNode(int value) {
this.value = value;
}
public SortNode getLeftNode() {
return leftNode;
}
public void setLeftNode(SortNode leftNode) {
this.leftNode = leftNode;
}
public SortNode getRightNode() {
return rightNode;
}
public void setRightNode(SortNode rightNode) {
this.rightNode = rightNode;
}
/**
* 添加二叉排序树
*
* @param node
*/
public void add(SortNode node) {
if (node == null) {
return;
}
//判断当前节点的大小
if (node.getValue() < this.getValue()) {
if (this.getLeftNode() == null) {
this.setLeftNode(node);
} else {
this.getLeftNode().add(node);
}
} else {
if (this.getRightNode() == null) {
this.setRightNode(node);
} else {
this.getRightNode().add(node);
}
}
//查询是否是平衡二叉树
//进行右旋转
if (leftHeigtht() - rightHeigth() >= 2) {
//双旋转
if (leftNode!=null&&leftNode.leftHeigtht()<leftNode.rightHeigth()){
leftNode.leftRatate();
}else {
//当前节点变成左节点的右节点
rightRatate();
}
} else {
//双旋转
if (rightNode!=null&&rightNode.rightHeigth()<rightNode.leftHeigtht()){
rightNode.rightRatate();
}else {
//左旋转
leftRatate();
}
}
}
/**
* 左旋转
*/
private void leftRatate() {
SortNode node = new SortNode(this.getValue());
node.setLeftNode(this.getLeftNode());
node.setRightNode(this.getRightNode().getLeftNode());
this.setValue(this.getRightNode().getValue());
this.setRightNode(this.getRightNode().getRightNode());
this.setLeftNode(node);
}
/**
* 右旋转
*/
private void rightRatate() {
SortNode node = new SortNode(this.getValue());
//当前节点的右节点赋值给新节点的右节点
node.setRightNode(this.getRightNode());
//将新节点加入当前节点的左节点的右子树
node.setLeftNode(this.getLeftNode().getRightNode());
//将当前节点的值换成左子节点的值
this.setValue(this.getLeftNode().getValue());
//将当前节点指向左节点的左节点
this.setLeftNode(this.getLeftNode().getLeftNode());
//将当前节点的右子树设置为新节点
this.setRightNode(node);
}
/**
* 左子树高度
*
* @return
*/
public int leftHeigtht() {
return this.getLeftNode()!=null?height():0;
}
/**
* 右子树高度
*
* @return
*/
public int rightHeigth() {
return this.getRightNode()!=null?height():0;
}
/**
* 返回前台节点的高度
*
* @return
*/
public int height() {
SortNode leftNode = this.getLeftNode();
SortNode rightNode = this.getRightNode();
return Math.max(leftNode == null ? 0 : leftNode.height(), rightNode == null ? 0 : rightNode.height()) + 1;
}
/**
* 中序遍历二叉排序树
*/
public void middleShow(SortNode node) {
if (node == null) {
return;
}
middleShow(node.getLeftNode());
System.out.println(node.getValue());
middleShow(node.getRightNode());
}
/**
* @param value
* @return
*/
public SortNode search(int value) {
if (this.getValue() == value) {
return this;
}
if (this.getValue() > value) {
return this.getLeftNode().search(value);
}
if (this.getValue() < value) {
return this.getRightNode().search(value);
}
return null;
}
/**
* 搜索父节点
*
* @param value
*/
public SortNode searchParent(int value) {
if (this.getLeftNode() != null && this.getLeftNode().getValue() == value ||
this.getRightNode() != null && this.getRightNode().getValue() == value) {
return this;
} else {
if (this.value < value && this.getLeftNode() != null) {
return this.getLeftNode().searchParent(value);
}
if (this.value > value && this.getRightNode() != null) {
return this.getRightNode().searchParent(value);
}
}
return null;
}
}








 本文介绍了平衡二叉树(AVL树)的概念,旨在解决二叉排序树的效率问题。平衡标准是任意节点的左右子树高度差不超过1。文章详细阐述了单旋转(右旋和左旋)和双旋转的原理,并通过实例说明如何通过旋转保持树的平衡。最后,讨论了如何用Java实现AVL树的旋转操作。
本文介绍了平衡二叉树(AVL树)的概念,旨在解决二叉排序树的效率问题。平衡标准是任意节点的左右子树高度差不超过1。文章详细阐述了单旋转(右旋和左旋)和双旋转的原理,并通过实例说明如何通过旋转保持树的平衡。最后,讨论了如何用Java实现AVL树的旋转操作。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








