数据结构之：八常用排序算法总结

常用排序算法

了解数据结构，对于我们开发者而言是非常必要的，而排序算法更是我们必须要了解和掌握的知识，在这里我总结了八种常用的排序算法以及自己学习排序算法的一些心得，希望对读者们有一定的帮助。（注：代码实现部分我是用java代码展示的）。废话不多说，下面就一起学习吧。

一、交换排序

交换排序中主要有：
1、冒泡排序；
2、快熟排序

1、冒泡排序

动态排序图如下：

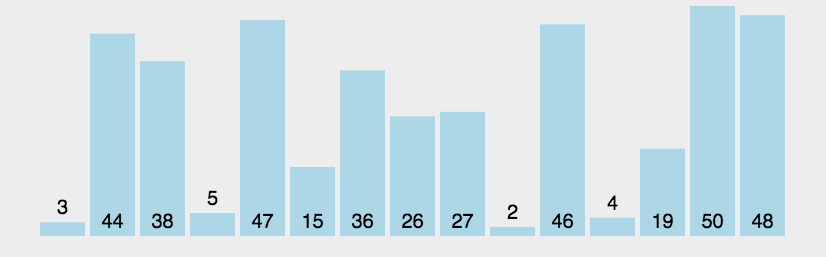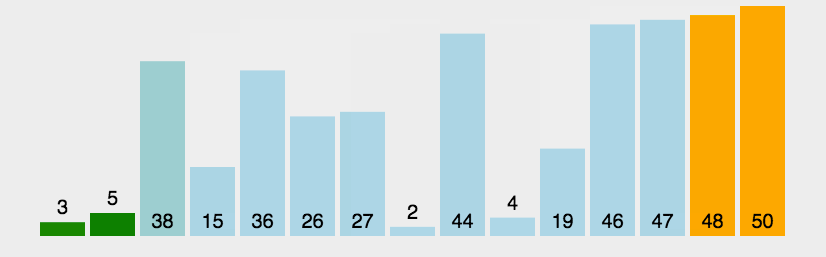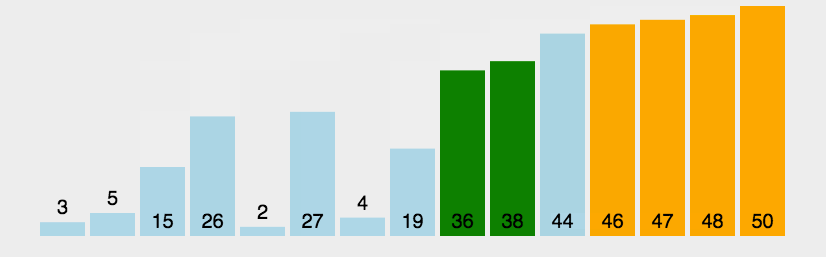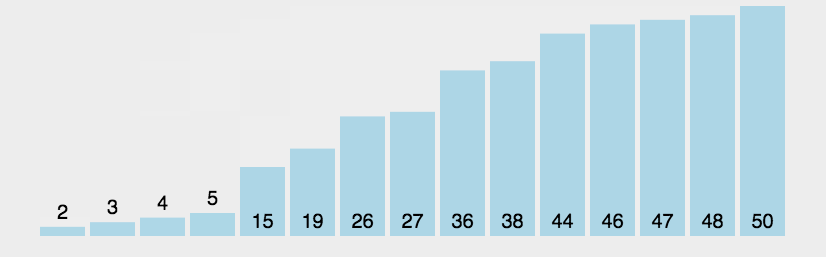
冒泡排序是我们接触开发的时候最先了解的一种排序算法，这种排序的思想就是从元素的起始位置开始，俩俩相邻的两组元素做对比，如果是升序排序，那么前者比后者大的话就交换顺序，直到元素变成有序为止，这种排序的规则有点像沸腾的水中的水泡从下向上的过程，因此我们叫这种排序算法为冒泡排序，排序算法是一种稳定的算法，它的代码实现也比较简单，就是两个for循环实现，接下来我们来看代码：

    /**
     * 冒泡排序
     * @param array
     */
    private static void bubbleSort(int[] array){
        if (array == null){
            return;
        }
        //第一个循环控制比较的轮数
        for (int i = 0; i < array.length-1; i++) {
            //控制的每一次冒泡的比较次数
            for (int j = 0; j < array.length-1-i; j++) {
                if (array[j]>array[j+1]){
                   int temp = array[j];
                    array[j] = array[j+1];
                    array[j+1] = temp;
                }
            }
        }

    }

2、快速排序

它的同态排序图如下：

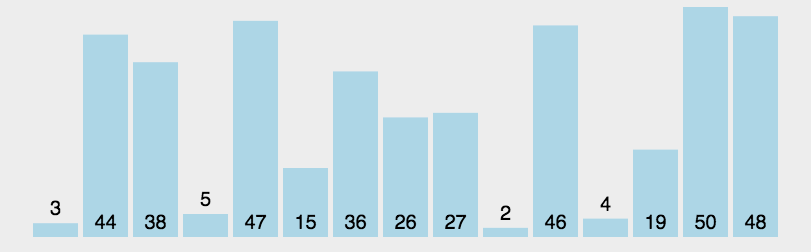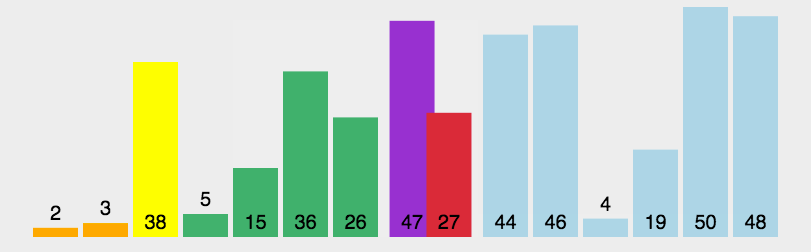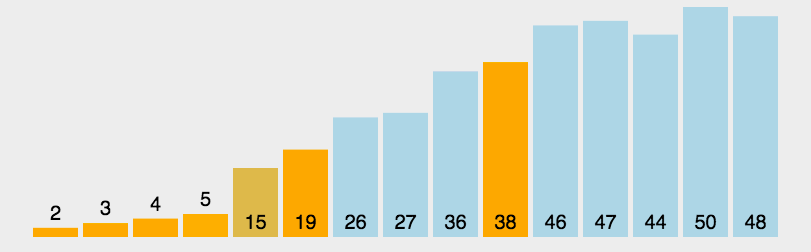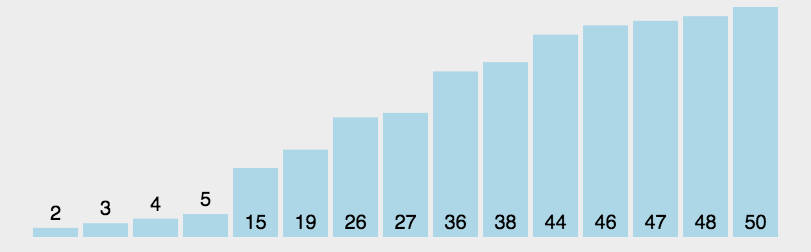
快速排序的排序思想就是随机选择我们要排序元素中的一个元素，一般我们默认选择起始位置的那个元素，排序规则就是：我们将选择的这个元素作为一个基准数，如果比这个元素大的，我们就往右边放，比基准数小的，就往左边放，当将所有元素遍历完之后，就分为了两个区，将左边的数和右边的数按照排序规则继续递归排序，就得到了一个有序的数组

代码实现如下：

private static void quickSort(int[] arry, int start, int end) {
        if (start >= end) {
            return;
        }
        //通常将数组的第一个元素作为标准数
        int startNumber = arry[start];
        //记录排序的下标
        int low = start;
        int high = end;
        //循环找比标准数大的数，比标准数小的数
        while (low < high) {
            while (low < high && startNumber <= arry[high]) {
                high--;
            }
            //使用右边的数替换左边的数
            arry[low] = arry[high];
            //如果左边的数比标准数小
            while (low < high && arry[low] <= startNumber) {
                low++;
            }
            arry[high] = arry[low];

        }
        //把标准数赋值给低位所在的元素
        arry[high] = startNumber;
        //递归所有小的数字
        quickSort(arry, start, low);
        //递归所有大的数字
        quickSort(arry, low + 1, end);

    }

二、插入排序

插入排序分为：
1、直接插入排序；
2、希尔排序

1、直接插入排序

插入排序动态展示图：

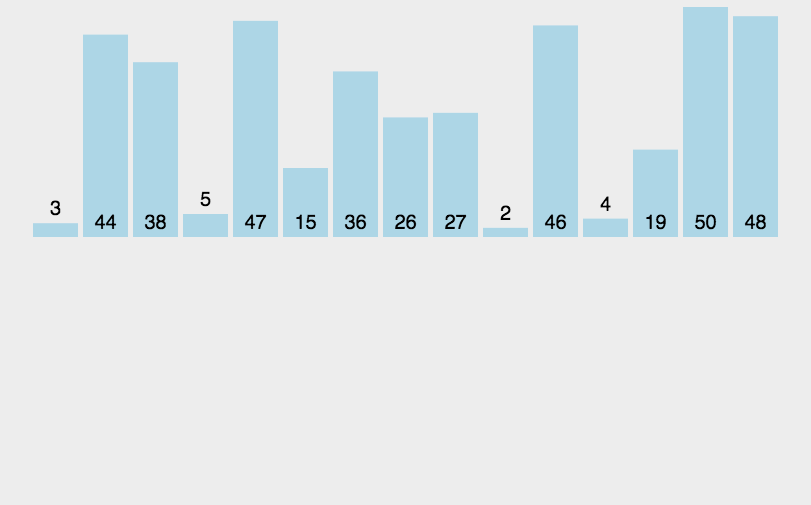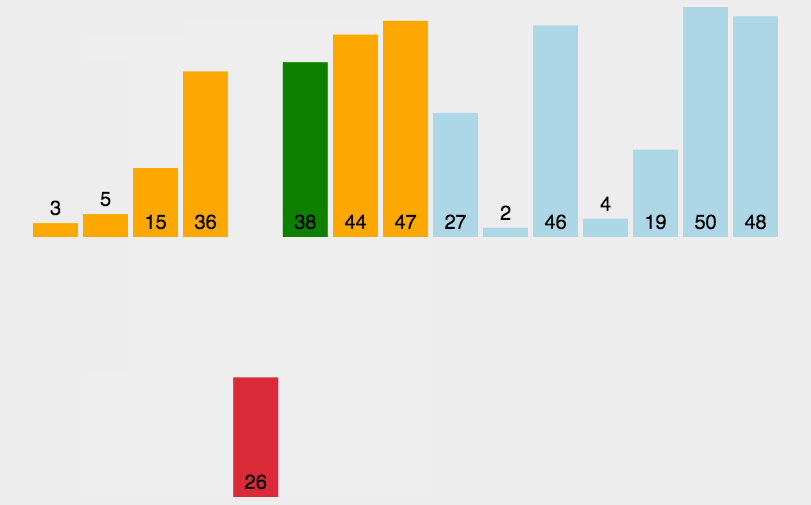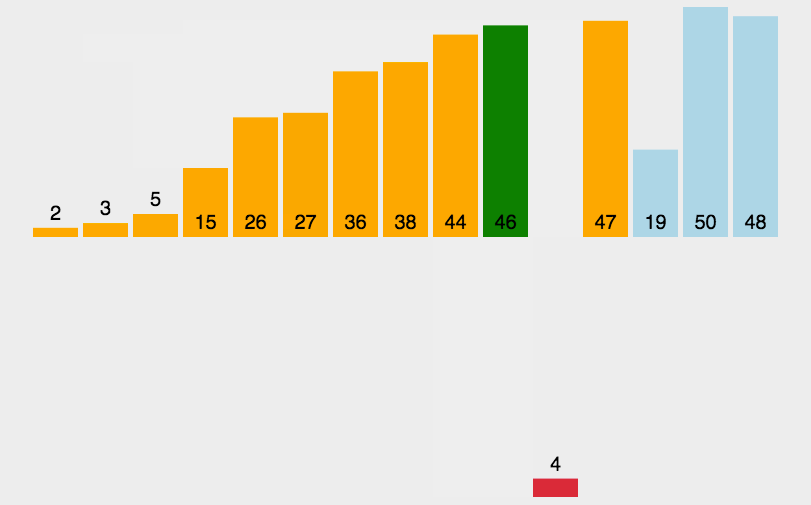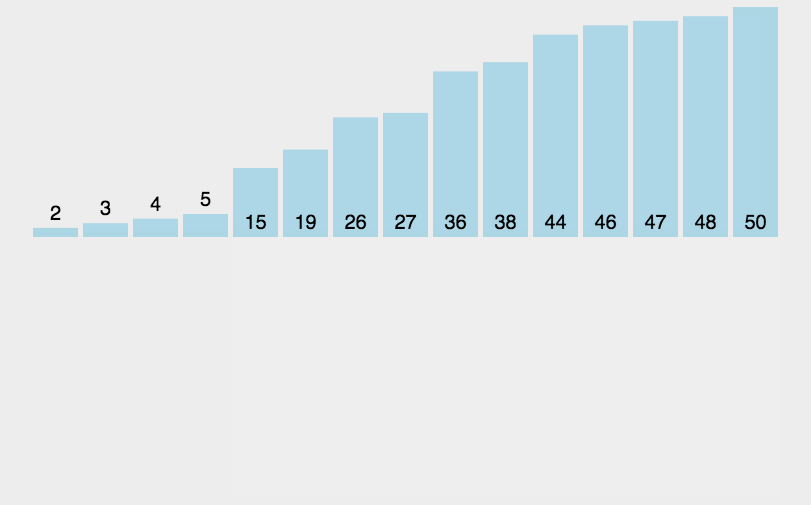
插入排序的算法原理很好理解，就是我们认定前面的元素都已经是有序的元素，后面的元素跟相邻前面的元素比较，如果比前者小，那么向前插入，并继续和前一个比较，直到找到正确的位置为止。这种排序和冒泡排序有相似之处，只不过冒泡是向后面比较，插入是向前面比较。

代码实现如下：

 private static void insertSort(int[] arra) {
        //直接插入排序默认前面的值已经是排好序的
        for (int i = 1; i <arra.length ; i++) {
            //存储当前遍历的数字
            int temp = arra[i];
            //如果前面的一个数比当前的小则进入排序
            if (arra[i]<arra[i-1]){
                int j=0;
                //循环排序
                for (j = i-1; j <i&&temp<arra[j] ; j--) {
                    arra[j+1] = arra[j];
                }
                //将临时变量的值还给被覆盖的值
                arra[j+1] = temp;
            }
        }

    }

2、希尔排序

动态展示图：

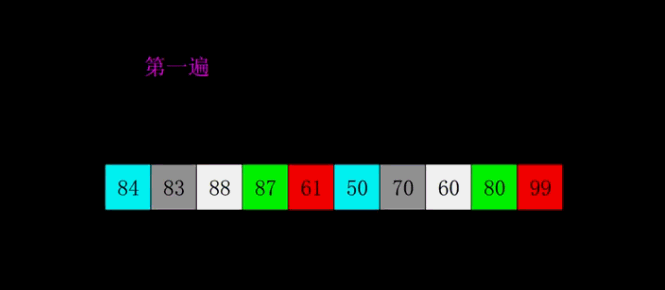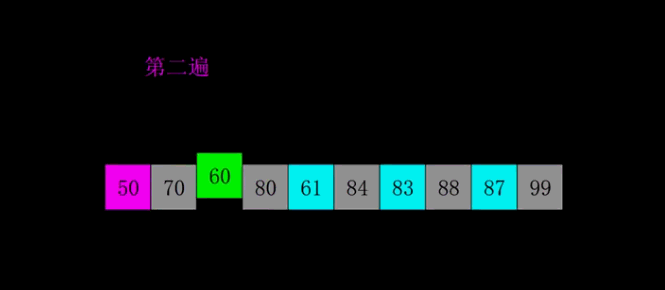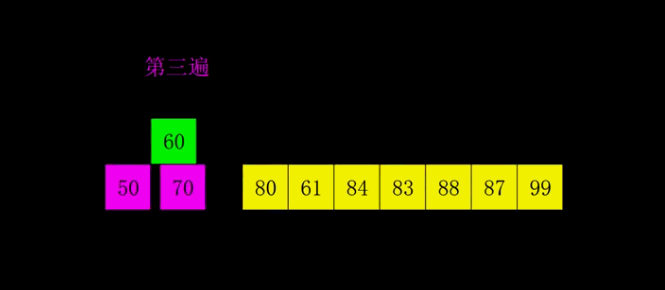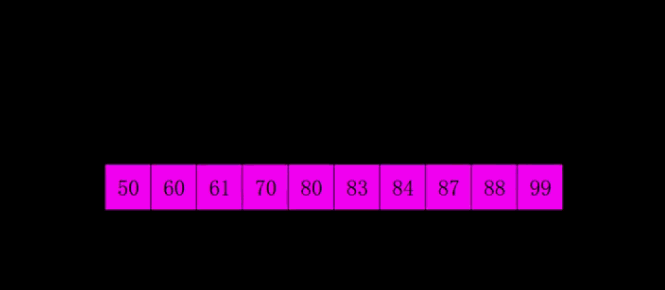
希尔排序其实是对我们的直接插入排序做了一点改进，在直接插入排序的思想上加了一个步长概念，先按照元素数量/2作为步长做一次插入排序，下一次的循环又按照上一次的步长/2再进行插入排序，直到步长为0结束排序。

代码实现：

    private static void shellSort(int[] arra) {
       //希尔排序，遍历所有步长,直到步长为0为止
        for (int d =  arra.length/2;d>0; d/=2) {
            //遍历所有元素
            for (int i = d; i <arra.length ; i++) {
                //按照步长遍历本组中的所有元素
                for (int j = i-d; j >=0 ; j-=d) {
                    //如果当前元素大于加步长后的那个元素
                    if(arra[j]>arra[j+d]){
                        int temp = arra[j];
                        arra[j] = arra[j+d];
                        arra[j+d] = temp;
                    }
                }
            }
        }

    }

三、选择排序

选择排序分为:
1、简单选择排序
2、堆排序

1、简单选择排序

动态展示图：

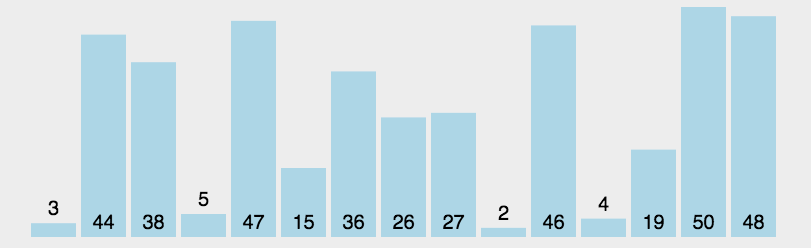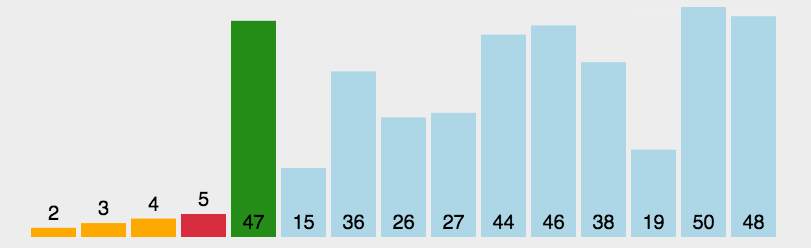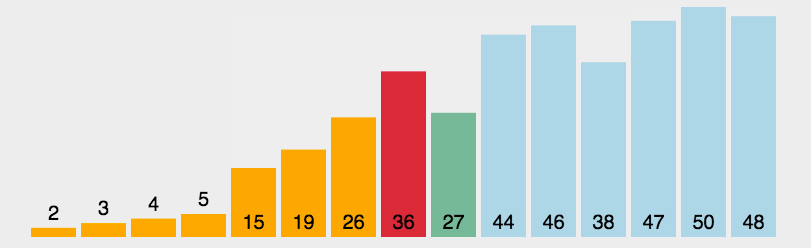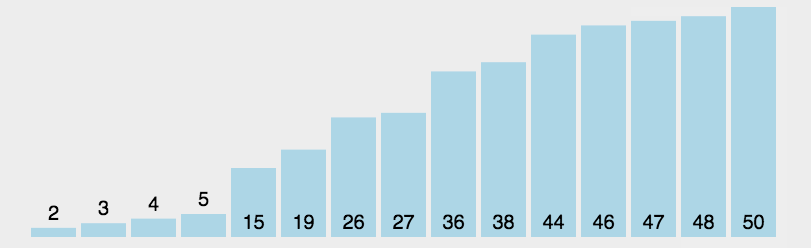
选择排序的算法思想比较简单，就是遍历元素，将最小的取出后，继续遍历选择最小的，直到取完元素为止，依次取出的元素便是排序后的元素

代码实现：

    private static void simpleChooseSort(int[] arra) {
       //简单选择排序
        for (int i = 0; i <arra.length; i++) {
            int minIndex = i;
            //遍历后面的元素，扎到最小的那个元素的下标
            for (int j = i+1; j <arra.length ; j++) {
                //循环记录数组中最小的元素
                if (arra[minIndex]>arra[j]){
                    minIndex = j;
                }
            }
            //赋值最小的元素Heapsort
           if (arra[minIndex] != arra[i]){
               int tmp = arra[i];
               arra[i] = arra[minIndex];
               arra[minIndex] = tmp;
           }

        }
    }

2、堆排序

动态展示图：

堆排序的算法思想就是将我们的元素先转换成大顶堆，（如果对大顶堆不熟悉，可以找度娘学习一波），转换成大顶堆之后，取第一个元素（即最大的元素），继续将取出元素后的二叉树转成大顶堆，重复以上逻辑，直到元素取完为止，我们可以获取一个降序的元素，反遍历一次就得到升序的元素

代码实现如下：

public class Heapsort {
   public static void main(String[] args) {
       int[] arra = new int[]{2, 7, 4, 10, 4, 8, 5};
       System.out.println(Arrays.toString(arra));
       //开始位置为最后一个非叶子节点
       int start = (arra.length-1)/2;
       //结束位置，数组的长度减一
       for (int i = start; i >=0 ; i--) {
           maxHeap(arra,arra.length,i);
       }
       //转成大顶堆之后，将大顶堆第一个元素放进数组的最后一个位置，再将前面的数又转换成大顶堆
       for (int i = arra.length -1; i >0; i--) {
           int temp = arra[0];
           arra[0] = arra[i];
           arra[i] = temp;
           maxHeap(arra,i,0);
       }
       System.out.println(Arrays.toString(arra));
   }

   public static void maxHeap(int[] arra, int size, int index) {
       //通过索引找到两个节点
       //左子节点
       int leftNode = index * 2 + 1;
       //右子节点
       int rightNode = index * 2 + 2;
       int max = index;
       //和两个子节点对比，找出最大的节点
       if (leftNode<size&&arra[leftNode] > arra[max]) {
           max = leftNode;
       }
       if (rightNode<size&&arra[rightNode] > arra[max]) {
           max = rightNode;
       }
       if (max != index) {
           int temp = arra[index];
           arra[index] = arra[max];
           arra[max] = temp;
           //交换位置后破快了之前的顺序，需要重新排序
           maxHeap(arra,size,max);
       }

   }
}

四 、归并排序

动态排序图：

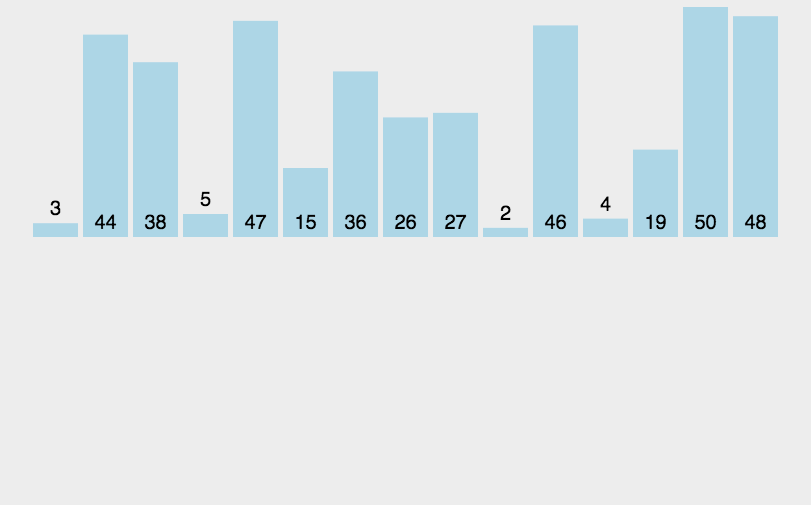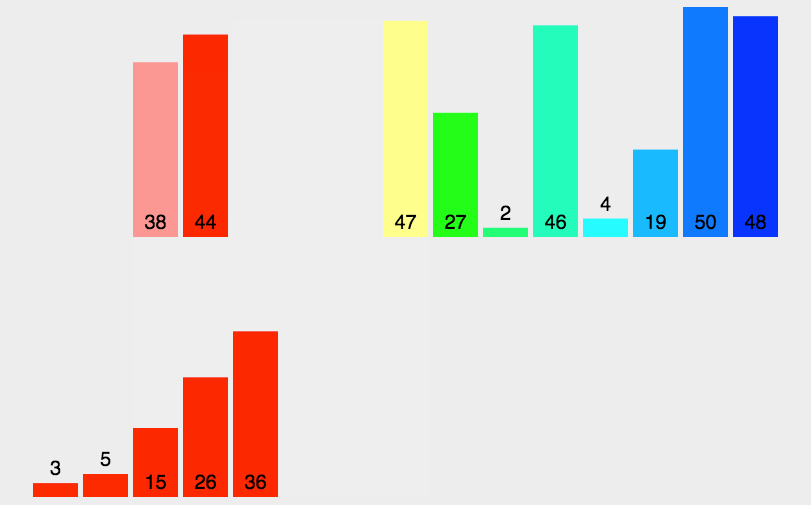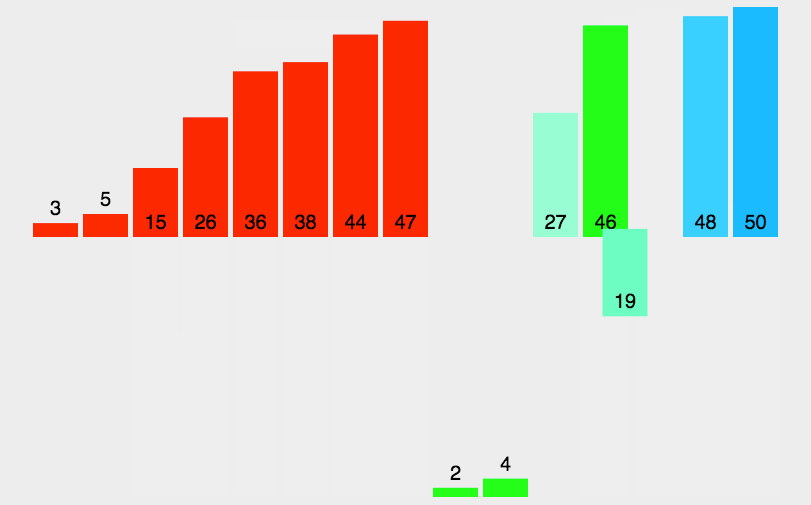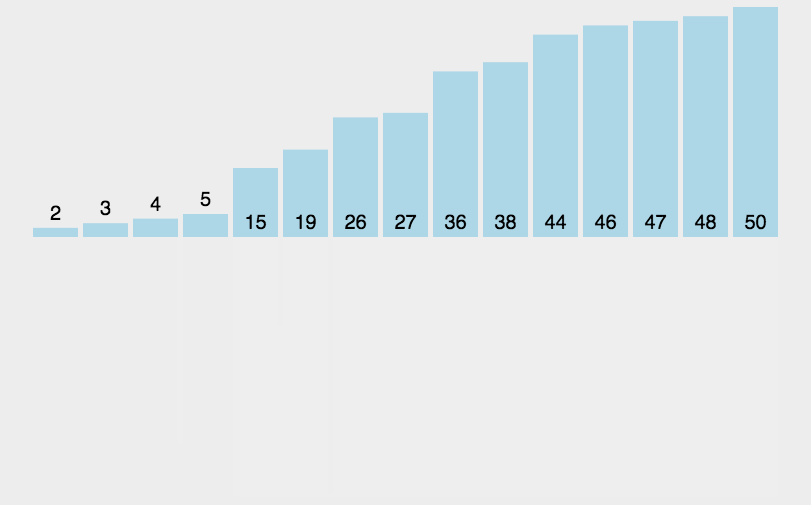
归并排序采用了递归的思想：将元素拆分为最小的两个数组，将两个数组归并排序（即升序合并到一个数组中），然后合并后的数组继续跟另外一个合并的数组继续比较合并，递归操作，直到排序完成

代码实现如下：

import java.util.Arrays;

/**
* 归并排序
*/
public class MergeSort {
   public static void main(String[] args) {
       int[] arra = new int[]{212,37,54,10,4,688,5,87,89,23,43,51};
       System.out.println(Arrays.toString(arra));
       mergeSort(arra,0,arra.length-1);

       System.out.println(Arrays.toString(arra));
   }

   private static void mergeSort(int[] arra,int low,int heigh) {
       if (low>=heigh){
           return;
       }
       int middel = (low+heigh)/2;
       //递归排序左边的数组
       mergeSort(arra,low,middel);
       //递归排序右边的数组
       mergeSort(arra,middel+1,heigh);
       //合并数组
       merge(arra,low,middel,heigh);
   }

   /**
    *
    * @param arra
    * @param low
    * @param middle
    * @param heigh
    */
   private static void merge(int[] arra,int low,int middle,int heigh) {
       //存放临时数组
       int[] temp = new int[heigh-low+1];
       //记录数组的下标
       int indexLow = low;
       //记录右边数组需要遍历的下标
       int indexHeight = middle+1;
       //记录临时数组的下标
       int tempIndex = 0;
       while (indexLow<=middle&&indexHeight<=heigh){
           //第一个数据更小
           if (arra[indexLow]<=arra[indexHeight]){
               //把小的数组放入临时数组中
               temp[tempIndex] = arra[indexLow];
               indexLow++;

           }else {
               temp[tempIndex] = arra[indexHeight];
               indexHeight++;
           }
           tempIndex++;
       }
       //处理多余的数
       while (indexLow<=middle){
           temp[tempIndex] = arra[indexLow];
           tempIndex++;
           indexLow++;
       }
       while (indexHeight<=heigh){
           temp[tempIndex] = arra[indexHeight];
           indexHeight++;
           tempIndex++;
       }
       //将临时的数组存入原数组
       for (int i = 0; i < temp.length; i++) {
           arra[i+low] = temp[i];
       }

   }
}

五、基数排序

动态图如下：

基数排序根据元素的位数进行排序，申请0-9的队列空间，第一次按照个数遍历，将元素各位相同的数有序的放在对应标记的队列中，第一次遍历结束后，从0-9的队列中按照存入的顺序依次取出，第二次按照十位遍历，执行相同的逻辑，直到遍历到最高位，循环结束。

代码实现如下：
1、数组版本

 private static void radxiSort(int[] arra) {
       //存数组中最大的数
       int max = Integer.MIN_VALUE;
       for (int arr:arra) {
           if (arr>max){
               max = arr;
           }
       }
       //计算最大的数字是几位数
       int maxLength = String.valueOf(max).length();
       //根据最大的长度决定比较次数
       int bucket[][] = new int[10][arra.length];
       //记录存放的个数
       int[] counts = new int[10];
       for (int i = 0,n=1; i < maxLength; i++,n*=10) {
           //把每一个数字求余
           for (int j = 0; j < arra.length; j++) {
              int remainder =  arra[j]/n%10;
               bucket[remainder][counts[remainder]] = arra[j];
               //记录数据
               counts[remainder]++;
           }
           //记录取元素的下标
           int index = 0;
           //把数字取出来
           for (int j = 0; j <counts.length; j++) {

               if (counts[j]!=0){
                   //循环取出元素
                   for (int k = 0; k < counts[j]; k++) {
                       arra[index] = bucket[j][k];
                       index++;
                   }
               }
               counts[j] = 0;
           }
       }
   }

2、队列版本

 private static void radxiSort(int[] arra) {
       //存数组中最大的数
       int max = Integer.MIN_VALUE;
       for (int arr:arra) {
           if (arr>max){
               max = arr;
           }
       }
       //计算最大的数字是几位数
       int maxLength = String.valueOf(max).length();
       Queue<Integer>[] queue = new Queue[10];
       for (int i = 0; i < 10; i++) {
           queue[i] = new ArrayDeque();
       }
       //记录存放的个数
       int[] counts = new int[10];
       for (int i = 0,n=1; i < maxLength; i++,n*=10) {
           //把每一个数字求余
           for (int j = 0; j < arra.length; j++) {
               int remainder =  arra[j]/n%10;
               queue[remainder].add(arra[j]);
               counts[remainder]++;
           }
           //将队列中的数按照顺序放入原来的数组中去
           int index = 0;
           for (Queue<Integer> queue1:queue) {
               while (!queue1.isEmpty()){
                   arra[index++] = queue1.poll();
               }
           }
       }
   }