梯度消失和梯度爆炸的理解以及解决办法

本文探讨了反向传播过程中导致梯度消失和梯度爆炸的原因，如sigmoid激活函数的导数乘积和权重初始化。解决策略包括预训练、梯度剪切、使用ReLU激活函数、BatchNormalization、残差网络以及LSTM。ReLU函数因其在正数部分的恒定导数1，有助于缓解深层网络的梯度消失问题，但其负数部分可能导致神经元死亡。BatchNormalization通过对输入进行规范化，增强梯度并加速训练。残差模块通过短路机制帮助信息直接传递，防止梯度消失。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

BP算法思路：

损失函数对第 $l-1$ 层到第 $l$ 层的权重矩阵求偏导等于损失函数对第 $l$ 层神经元状态值的误差项乘以相应的第 $l-1$ 层的神经元的激活值。

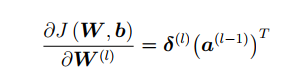
其中损失函数对第 $l$ 层神经元状态值的误差项可以通过如下式子计算，

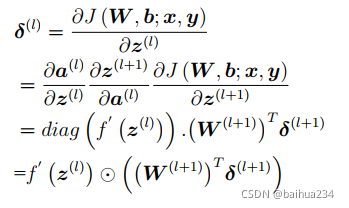
即第 $l$ 层神经元的误差项是与所有与该神经元相连接的 $l+1$ 层神经元的误差项的加权和再乘以该神经元激活函数的梯度计算得到的。

BP神经网络计算过程：（1）输入信号通过前向传播算法依次计算输入层、若干中间层和输出层中所有神经元的状态值和激活值。（2）根据输出层的预测结果和真实的样本标签计算误差函数值，并利用后向传播算法将误差值进行后向传播计算，得到每一层神经元的误差项。（3）根据误差项和激活值可以计算目标函数关于所有训练参数的偏导数，进而根据梯度下降算法可以进行参数更新。

梯度消失与梯度爆炸：

梯度消失是因为反向传播过程中对梯度的求解会产生sigmoid导数和参数的连乘，sigmoid导数的最大值为0.25，权重一般初始都在0，1之间，乘积小于1，多层的话就会有多个小于1的值连乘，导致靠近输入层的梯度几乎为0，得不到更新。梯度爆炸是也是同样的原因，只是如果初始权重大于1，或者更大一些，多个大于1的值连乘，将会很大或溢出，导致梯度更新过大，模型无法收敛。

解决梯度消失或者梯度爆炸的方法：

1.预训练；

2.梯度剪切、正则（主要是通过限制权重矩阵的大小解决梯度爆炸的问题）；

3.改变激活函数：（1）tanh激活函数不能有效改善梯度消失或者梯度爆炸问题；（2）Relu函数的导数在整数部分是恒等于1的，因此在深层网络中使用Relu激活函数不会导致梯度消失问题。“疑问1：部文章中说Relu函数可以解决梯度爆炸问题？？？关于这一点怎么理解；疑问2：文章中说Relu函数负数部分恒为0，会导致一些神经元无法激活，可以通过设置小学习率部分解决？？？怎么理解”

4.Batch Normalization：BN层就是对每一层的输出做scale和shift的操作，即通过一定的规范化手段把神经元的输入值分布强行拉回到接近均值为0方差为1的标准正态分布中，这样使得输入值落在激活函数对输入比较敏感的区域，输入值的微小变化就会引起损失函数较大的变化，即梯度变大，从而避免了梯度消失。此外，梯度变大意味着学习收敛速度快，可以大大加快训练速度。

5。残差模块：参考链接https://blog.youkuaiyun.com/Tink1995/article/details/105080033?utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-10.essearch_pc_relevant&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-10.essearch_pc_relevant中关于残差网络的描述。

6.LSTM：首先学习通过该文章学习RNN梯度消失和爆炸的原因,CNN各个参数矩阵的梯度是独立的，该消失就是会消失，越靠近输入层的权重，梯度消失或者梯度爆炸的可能性越大；RNN的特殊性在于它的权重是共享的，每一时刻的梯度是由前面所有时刻共同决定的，是一个相加的过程，当距离过长时，最前面的梯度会消失或者爆炸，但是当前时刻的梯度不会消失或者爆炸，通常人们所说的RNN梯度消失或爆炸，是指当下梯度更新用不到前面的梯度了。这篇文章回答了LSTM如何解决梯度消失的问题。