Java中浮点数的精确度探讨

Java中浮点数不精确的讨论
1.十进制中数的表示

我们知道，在十进制中，有些小数是不能被精确便表示的，比如
· 3^(-1)次方，即1/3，这个数是不能使用十进制精确表示的，只能表示为无限循环小数0.333333333333…

2.同一个数在不同进制的表示

同样还以3^(-1)次方为例，其在十进制中不能精确表示，但如果是三进制呢？三进制逢三进一，即整数3在三进制中的表示就是 10（三进制），因此可以得出3^(-1)即1/3在三进制中的表示

· 十进制 3^(-1) --> 三进制 10^(-1)，其表示为三进制小数为 0.1(三进制)

也就是说1/3这个数可以在三进制中被精确表示而不能在十进制中被精确表示。

同样的道理，有些在十进制中可以准确表示的数，在二进制中是不一定能够准确表示的。

3.十进制到二进制的小数转换

对于二进制来说，二进制小数点右边能表达的值是 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128 … 1/(2^n）

我们来试一试如何表达十进制的 0.2 吧。

      0.01(二进制) = 1/4(十进制) = 0.25(十进制) ,太大

      0.001(二进制) =1/8(十进制) = 0.125(十进制) , 太小

      ...同理得下列推算，不再标明进制符号

      0.0011 = 1/8 + 1/16 = 0.1875 , 逼近0.2了

      0.00111 = 1/8 + 1/16 + 1/32 = 0.21875 , 又大了

      0.001101 = 1/8+ 1/16 + 1/64 = 0.203125 还是大

      0.0011001 = 1/8 + 1/16 + 1/128 = 0.1953125 这结果不错

      0.00110011 = 1/8+1/16+1/128+1/256 = 0.19921875 已经很逼近了

其实这就是我们学过逼近法来找到最相近的值，同理计算机是无法准确表示十进制小数0.2的。所以一般要求极其精确的计算时，一般都用java.math.BigDecimal来进行处理，不过对于日常的科学计算，浮点数已经足够了。

4.实例验证
首先我们通过一个判断语句来验证

package cn.theo.java.learn;

public class DoublePrecision {
    public static void main(String[] args) {
        if(0.3-0.1==0.2)
            System.out.println("0.3-0.1==0.2 is right");
        else
            System.out.println("0.3-0.1==0.2 is incorrect");
    }
}

如果计算机中0.3-0.10.2则输出"0.3-0.10.2 is right"，若0.3-0.1!=0.2则输出"0.3-0.1==0.2 is incorrect"
输出结果如下：

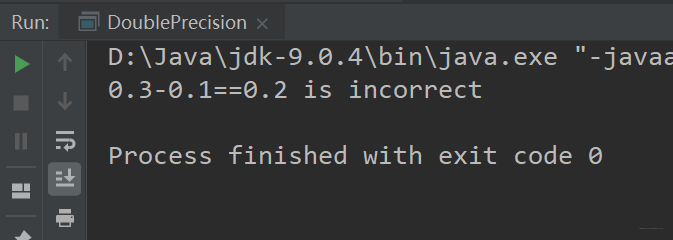
再一次验证了在计算机中浮点数是不准确的。

让我们看一下计算机中，0.3-0.1的真实结果：

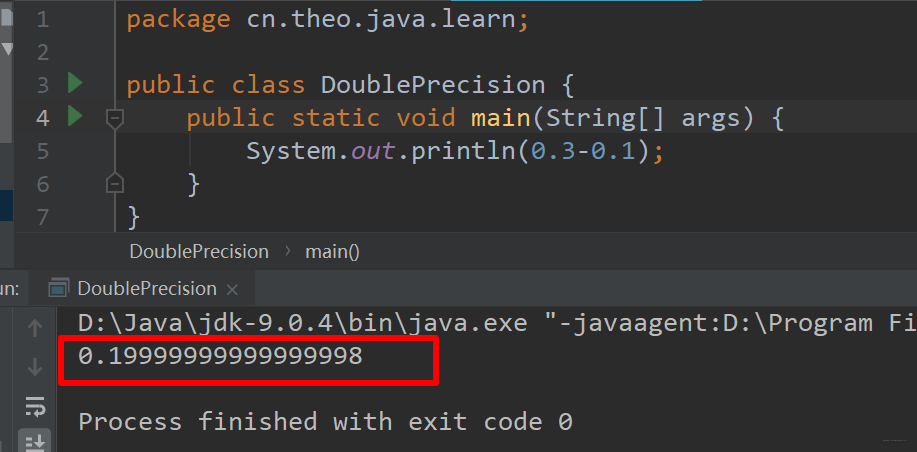
我们可以看到，真实的结果是0.19999999999999998（这也仅仅是近似值）

因此在精度要求不是特别高的科学计算时，我们一般都引入一个误差值来修正此问题，例如上面判断0.3-0.2==0.1的例子

可进行如下修改：

package cn.theo.java.learn;

public class DoublePrecision {
    public static void main(String[] args) {
        double decimal=0.00000001;
        if(0.3-0.1-0.2<=decimal)
            System.out.println("0.3-0.1==0.2 is right");
        else
            System.out.println("0.3-0.1==0.2 is incorrect");
    }
}

此时可在误差允许内进行逻辑判断。