基于自适应区域增长(ARGS)算法的平面三角网格剖分

本文链接：https://blog.youkuaiyun.com/baidu_40924225/article/details/100574992

基于自适应区域增长(ARGS)算法的平面三角网格剖分

· 主要思路

1 首先建立活动边表存储链表activeList，用于记录ARGS算法中边的信息。

2 定义种子三角面片SeedT,以种子三角片为核心，不断向周围扩张，查找种子三角片的方法为：在点云中随机找一个点point,然后获取r领域中的所有点，并根据到领域点到point的距离排序，选取距离最小的两个点作为三角片中的点，筛选种子三角片的条件如下：
(1) 三个点不在一条直线上。
(2) 三个点所构成的三角片内部不包含点云中其他的点。
(3) 领域点集中的其他点都在种子三角片的同一侧，此项约束能够保证种子三角片能够保证种子三角片的选取在点云曲面的外表面上。

3 获取候选点集以及最佳点BestP,首先得到当前活动边，以当前活动边为终点为源点，查找r领域中的领域点，通过计算这些点与活动边构建的新三角片的法向量与活动边对应的法向量的y值乘积来选取乘积小于0的一侧的点作为候选点集，接着对候选点集中的点计算代价并排序，选取代价最小的点为最佳点。

4 记录最佳点BestP和当前活动边所构成的新三角片，将新生成的两条边加入到当前活动边的位置，并从活动边表中删除当前活动边。

5 当前活动边表为空时，搜寻结束。

注意：搜索领域点本程序采用的PCL中内置的搜索领域算法。

· 实现代码

// 网格重建
vector ARGS::ArgsAlgorithm()
{
Surface Orgin, a,c1;
boost::shared_ptrpcl::visualization::PCLVisualizer view(new pcl::visualization::PCLVisualizer(“test”));
pcl::PointXYZ bestpoint;

vector<CEdge> activelist;

list<CEdge>active;
vector<CEdge> currentlist;
CEdge fixededge, currentedge;
Orgin = SelectSurface();
//Orgin.ToString();
int i1 = 0;
int i = 0;

// 将种子三角面片的三条边加入到活动边表active中，并在surfacelist中存储每一条边对应的三角面片
view->addLine(Orgin.edge1.startNode, Orgin.edge1.endNode, std::to_string(i1));
i1++;
view->addLine(Orgin.edge2.startNode, Orgin.edge2.endNode, std::to_string(i1));
i1++;
view->addLine(Orgin.edge3.startNode, Orgin.edge3.endNode, std::to_string(i1));
i1++;
// 将种子三角面片的边添加到活动边表中
active.push_front(Orgin.edge3);
active.push_front(Orgin.edge2);
surfacelist1.push_back(Orgin);
active.push_front(Orgin.edge1);

activelist.push_back(Orgin.edge1);
surfacelist.push_back(Orgin);
activelist.push_back(Orgin.edge2);
surfacelist.push_back(Orgin);

activelist.push_back(Orgin.edge3);
surfacelist.push_back(Orgin);
currentedge = active.front();
currentlist.push_back(currentedge);
a = surfacelist.front();
fixededge = Orgin.edge3;
c1 = Orgin;
do
{
	surfacelist1.push_back(a);
	// 获取最佳点（通过代价和新构建三角片与当前活动边所对应的三角片的法向量来确定最佳点，将所得代价排序，选取最小的点为最佳点）
	bestpoint = GetCandidate(currentedge, a);
	// 没有找到最佳点，需要进行出栈，然后选取栈顶元素为当前活动边
	if (flag == 1)
	{
		flag = 0;
		if (active.size() != 0||surfacelist.size()!=0)
		{
			active.pop_front();
			surfacelist.pop_front();
			currentedge.startNode = active.front().endNode;
			currentedge.endNode = active.front().startNode;
			continue;
		}
		else
			break;
	}
	// 找到最佳点后，以当前活动边以及最佳点最为新的三角片，并将新的三角片中的新的两条边加入到活动边表中，并更新当前活动边。
	CEdge edge2(bestpoint, currentedge.endNode), edge1(currentedge.startNode,bestpoint);

	a.edge1 = edge1;
	a.edge2 = edge2;
	a.edge3 = currentedge;
	a.p0 = currentedge.startNode;
	a.p1 = bestpoint;
	a.p2 = currentedge.endNode;
	if(active.size()>0)
	{
	active.pop_front();
	surfacelist.pop_front();
	active.push_front(edge2);
	surfacelist.push_front(a);
	active.push_front(edge1);
	surfacelist.push_front(a);
	}
	else break;


	currentedge = active.front();
	// 判断新生成的当前活动边是否已经为访问过的活动边，若已经访问过则出栈。
	while (count(currentlist.begin(),currentlist.end(), currentedge)>0)
	{
		active.pop_front();
		surfacelist.pop_front();
		currentedge = active.front();
	}
	// 当前活动边所对应的三角片
	a = surfacelist.front();
	// 记录已经访问过的活动边
	currentlist.push_back(currentedge);

	i++;
	std::cout <<"序号:"<< i << std::endl;

	


} while (!active.empty());
i = 0;

// 显示三角网格剖分结果
for (auto it = surfacelist1.begin();it != surfacelist1.end();it++)
{
	Surface a = *it;
	view->addLine(a.edge1.startNode, a.edge1.endNode,1,0,0, std::to_string(i1));
	
	i1++;
	view->addLine(a.edge2.startNode, a.edge2.endNode, 0, 1, 0, std::to_string(i1));
	i1++;
	view->addLine(a.edge3.startNode, a.edge3.endNode, 0, 0, 1, std::to_string(i1));
	i1++;
}
return surfacelist1;

}

## ·运行结果
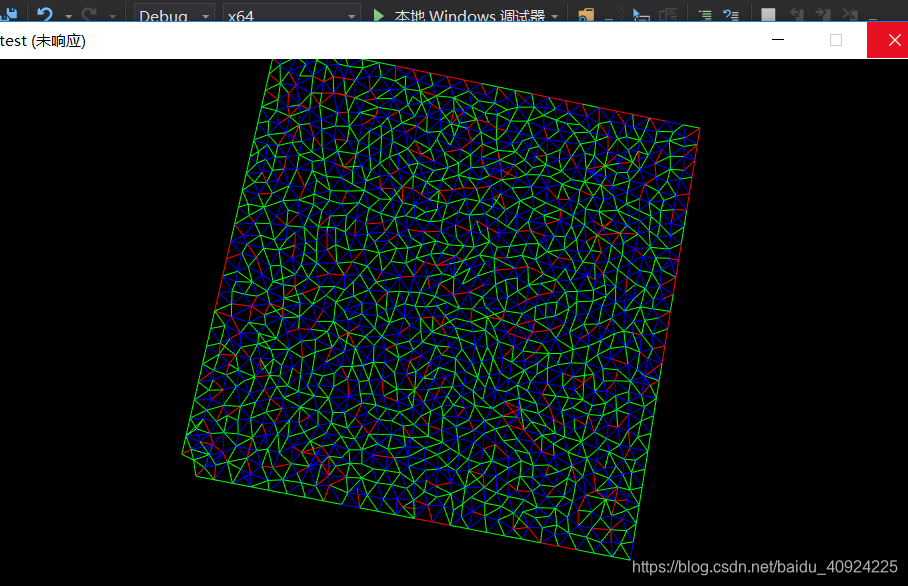
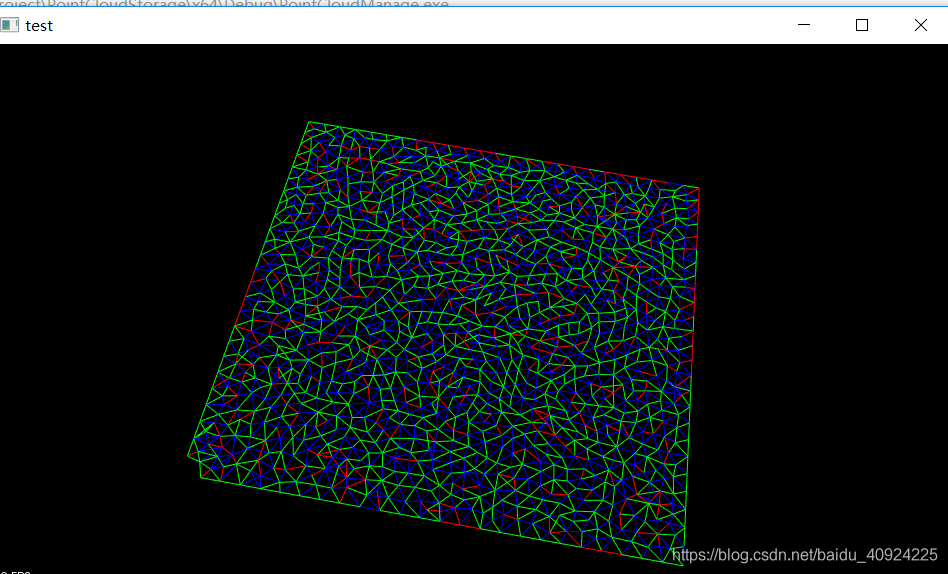
![在这里插入图片描述](https://img-blog.csdnimg.cn/20190906155145243.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2JhaWR1XzQwOTI0MjI1,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20190906155157892.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2JhaWR1XzQwOTI0MjI1,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20190906155206754.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2JhaWR1XzQwOTI0MjI1,size_16,color_FFFFFF,t_70)
## ·总结
这个任务有一定的难度，从配置vtk,pcl,qt到实现网格重建遇到了很多问题，但是都在同组小伙伴和我的不懈努力下得到了解决，虽然在这个过程中我们有很多意见分歧，但是都互相探讨，找出最优化的方案。