Learning Deformable Kernels in 3D GraphConvolution Networks for Point Cloud Analysis 阅读笔记

Task

定义一种在三维形状中，新的点云运算方法。

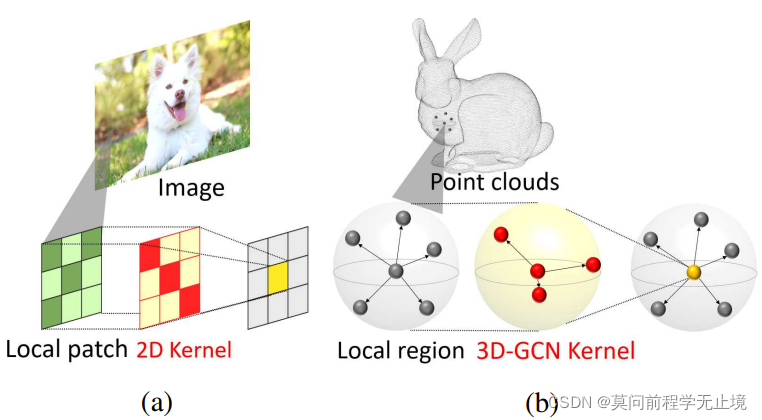
 问题

(1) 三维点云是一种无序，无结构的三维形状表达方式，因此不能提供一种统一的运算方式。

(2)之前的一些方法，在对三维点云进行一些操作，例如放缩和平移的时候，就会影响计算的效果。

解决方法

（1）利用一个可变形的3D核去学习3D点云的信息。

（2）提出了一个基于图的最大池化的方法去处理不同的尺度信息。

方法

 作者自定义了图卷积的感受野，即对于一个三维形状中的每一个点，作者固定了其周围的最近邻的M个点作为其感受野。此外，作者模仿2D CNN的图，做了一个类似的3D点云的Kernel。用这种方法去模拟卷积在二维上的操作。如上图右边所示，是定义的Kernel。

作者定义的GCN的公式：

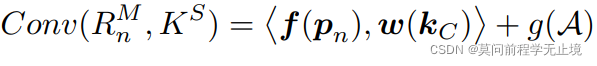
 即，对应的一个感受野和kernel的卷积操作。其中f(pn)代表的是点云形状中，每一个点的特征，Kc代表的是卷积核中的点。要计算内积，此外还需要计算两个点对应的向量的余弦相似度g（A），下图sim总结了计算过程。

 

 计算公式如下所示：

思索

记录一下我觉得比较新的几个点：

（1）将图像的patch和卷积核的相乘看作是求两者之间的相似度，从而去求算点云的向量间的余弦相似度

（2）感受野，将点云的感受野定义为一个小的graph内，点之间向量的集合。

问题：

我读完之后对核的来由不是特别清楚，文中说了一开始定义w(k) = 1。我猜猜是给定初始值，之后根据学习来进行调整。其次关于为什么要使用L个kernel，我现在还不是特别的清楚，我个人认为，如果与卷积类似，那么使用一个就足够了。下文作者也提到了，使用L个卷积是为了进行最大池化操作，我还没有特别理解

参考文献

[1] Lin Z H, Huang S Y, Wang Y C F. Convolution in the cloud: Learning deformable kernels in 3d graph convolution networks for point cloud analysis. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020: 1800-1809.

github: https://github.com/j1a0m0e4sNTU/3dgcn