机器学习2之回归

1.线性回归

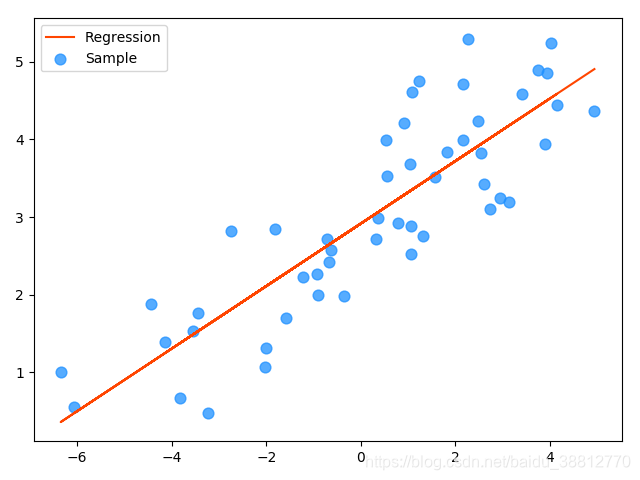
# 基于线性回归训练single.txt中的训练样本，使用模型预测测试样本。
import numpy as np
import sklearn.linear_model as lm
import matplotlib.pyplot as mp
# 采集数据
x, y = np.loadtxt('../data/ml_data/single.txt',
                  delimiter=',',
                  usecols=(0, 1),
                  unpack=True)
print(x)
x = x.reshape(-1, 1)
print(x)
# 创建模型
model = lm.LinearRegression()  # 线性回归
# 训练模型
model.fit(x, y)
# 根据输入预测输出
pred_y = model.predict(x)
mp.scatter(x, y, c='dodgerblue', alpha=0.75, s=60, label='Sample')
mp.plot(x, pred_y, c='orangered', label='Regression')
mp.legend()
mp.show()

# 误差估计
import sklearn.metrics as sm

# 平均绝对值误差：1/m∑|实际输出-预测输出|
print(sm.mean_absolute_error(y, pred_y))
# 平均平方误差：SQRT(1/mΣ(实际输出-预测输 出)^2)
print(sm.mean_squared_error(y, pred_y))
# 中位绝对值误差：MEDIAN(|实际输出-预测输出|)
print(sm.median_absolute_error(y, pred_y))
# R2得分，(0,1]区间的分值。分数越高，误差越小。
print(sm.r2_score(y, pred_y))

import pickle
# 将训练好的模型对象保存到磁盘文件中
with open('../../data/linear.pkl', 'wb') as f:
    pickle.dump(model, f)

# 从磁盘文件中加载模型对象

with open('../../data/linear.pkl', 'rb') as f:
    model = pickle.load(f)
# 根据输入预测输出
pred_y = model.predict(x)

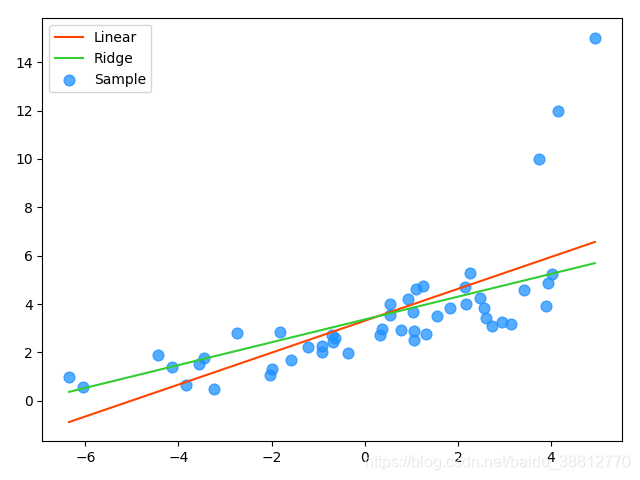
2.岭回归

"""
异常值对模型所带来影响无法在训练过程中被识别出来。为此，岭回归在模型迭代过程
所依据的损失函数中增加了正则项
"""
# 岭回归
x, y = np.loadtxt('../data/ml_data/abnormal.txt',
                  delimiter=',',
                  usecols=(0, 1),
                  unpack=True)
print(x)
x = x.reshape(-1, 1)
print(x)

# 创建线性模型
model = lm.LinearRegression()  # 线性回归
# 训练模型
model.fit(x, y)
# 根据输入预测输出
pred_y1 = model.predict(x)
# 创建岭回归模型
model = lm.Ridge(150, fit_intercept=True, max_iter=10000)
# 训练模型
model.fit(x, y)
# 根据输入预测输出
pred_y2 = model.predict(x)
sorted_indices = x.T[0].argsort()
mp.scatter(x, y, c='dodgerblue', alpha=0.75, s=60, label='Sample')
mp.plot(x[sorted_indices], pred_y1[sorted_indices],
        c='orangered', label='Linear')
mp.plot(x[sorted_indices], pred_y2[sorted_indices],
        c='limegreen', label='Ridge')

mp.legend()
mp.show()

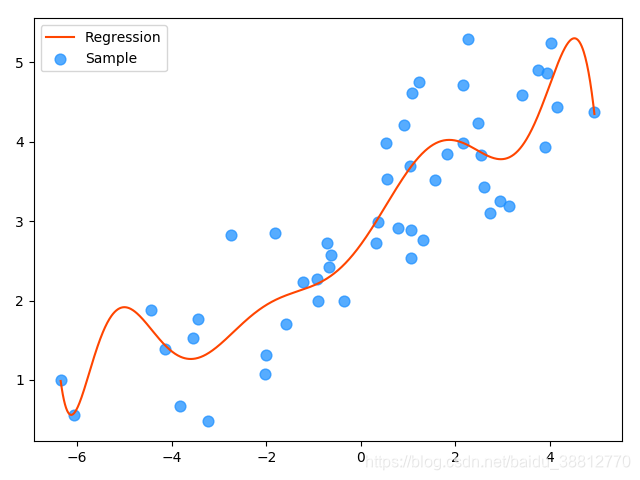
3.多项式回归

"""
所以一元多项式回归的实现需要两个步骤：

1. 将一元多项式回归问题转换为多元线性回归问题（只需给出多项式最高次数即可）。
2. 将1步骤得到多项式的结果中 参数
当做样本特征，交给线性回归器训练多元线性模型。
"""

import numpy as np
import sklearn.pipeline as pl
import sklearn.preprocessing as sp
import sklearn.linear_model as lm
import sklearn.metrics as sm
import matplotlib.pyplot as mp
# 采集数据
x, y = np.loadtxt('../data/ml_data/single.txt', delimiter=',', usecols=(0,1), unpack=True)
x = x.reshape(-1, 1)

# 创建模型(管线)
model = pl.make_pipeline(
    sp.PolynomialFeatures(10),
    lm.LinearRegression()
)
# 模型训练
model.fit(x, y)
# 根据输入预测输出
pred_y = model.predict(x)
test_x = np.linspace(x.min(), x.max(), 1000).reshape(-1, 1)
pred_test_y = model.predict(test_x)

mp.scatter(x, y, c='dodgerblue', alpha=0.75, s=60, label='Sample')
mp.plot(test_x, pred_test_y, c='orangered', label='Regression')
mp.legend()
mp.show()

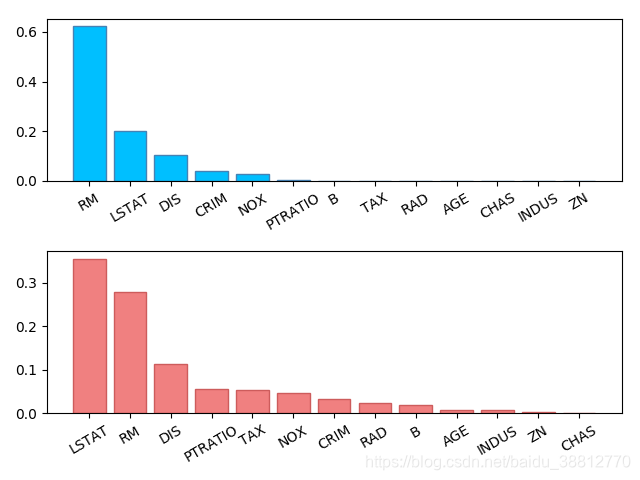
4.决策树

import sklearn.datasets as sd
import sklearn.utils as su

# 加载波士顿地区房价数据集
boston = sd.load_boston()
print(boston.feature_names)
# 打乱原始数据集的输入和输出
x, y = su.shuffle(boston.data, boston.target, random_state=7)

# 划分训练集和测试集
train_size = int(len(x) * 0.8)
train_x, test_x, train_y, test_y = \
    x[:train_size], x[train_size:], \
    y[:train_size], y[train_size:]

import sklearn.tree as st
import sklearn.metrics as sm
import sklearn.ensemble as se
# 创建决策树回归模型
model = st.DecisionTreeRegressor(max_depth=4)
# 训练模型
model.fit(train_x, train_y)
# 测试模型
pred_test_y = model.predict(test_x)
print(sm.r2_score(test_y, pred_test_y))         # 0.8202560889408634

import matplotlib.pyplot as mp
import numpy as np

model = st.DecisionTreeRegressor(max_depth=4)
model.fit(train_x, train_y)
# 决策树回归器给出的特征重要性
fi_dt = model.feature_importances_
model = se.AdaBoostRegressor(
    st.DecisionTreeRegressor(max_depth=4), n_estimators=400, random_state=7)
model.fit(train_x, train_y)
# 基于决策树的正向激励回归器给出的特征重要性
fi_ab = model.feature_importances_

mp.subplot(211)
sorted_indices = fi_dt.argsort()[::-1]
pos = np.arange(sorted_indices.size)
mp.bar(pos, fi_dt[sorted_indices], facecolor='deepskyblue', edgecolor='steelblue')
mp.xticks(pos, boston.feature_names[sorted_indices], rotation=30)

mp.subplot(212)
sorted_indices = fi_ab.argsort()[::-1]
pos = np.arange(sorted_indices.size)
mp.bar(pos, fi_ab[sorted_indices], facecolor='lightcoral', edgecolor='indianred')
mp.xticks(pos, boston.feature_names[sorted_indices], rotation=30)

mp.tight_layout()
mp.show()

"""
随机森林
在自助聚合的基础上，每次构建决策树模型时，不仅随机选择部分样本，
而且还随机选择部分特征，这样的集合算法，不仅规避了强势样本对预测结果的影响，
而且也削弱了强势特征的影响，使模型的预测能力更加泛化。
"""
# 分析共享单车的需求，从而判断如何进行共享单车的投放。
import numpy as np
import sklearn.utils as su
import sklearn.ensemble as se
import sklearn.metrics as sm
import matplotlib.pyplot as mp

data = np.loadtxt('../data/ml_data/bike_day.csv',
                  unpack=False, dtype='U20', delimiter=',')
day_headers = data[0, 2:13]
x = np.array(data[1:, 2:13], dtype=float)
y = np.array(data[1:, -1], dtype=float)

x, y = su.shuffle(x, y, random_state=7)
print(x.shape, y.shape)
train_size = int(len(x) * 0.9)
train_x, test_x, train_y, test_y = \
    x[:train_size], x[train_size:], y[:train_size], y[train_size:]

# 随机森林回归器
model = se.RandomForestRegressor(max_depth=10, n_estimators=1000, min_samples_split=2)
model.fit(train_x, train_y)
# 基于“天”数据集的特征重要性
fi_dy = model.feature_importances_
pred_test_y = model.predict(test_x)
print(sm.r2_score(test_y, pred_test_y))

data = np.loadtxt('../data/ml_data/bike_hour.csv',
                  unpack=False, dtype='U20', delimiter=',')

hour_headers = data[0, 2:13]
x = np.array(data[1:, 2:13], dtype=float)
y = np.array(data[1:, -1], dtype=float)
x, y = su.shuffle(x, y, random_state=7)
train_size = int(len(x) * 0.9)
train_x, test_x, train_y, test_y = \
    x[:train_size], x[train_size:], \
    y[:train_size], y[train_size:]
# 随机森林回归器
model = se.RandomForestRegressor(
    max_depth=10, n_estimators=1000,
    min_samples_split=2)
model.fit(train_x, train_y)
# 基于“小时”数据集的特征重要性
fi_hr = model.feature_importances_
pred_test_y = model.predict(test_x)
print(sm.r2_score(test_y, pred_test_y))

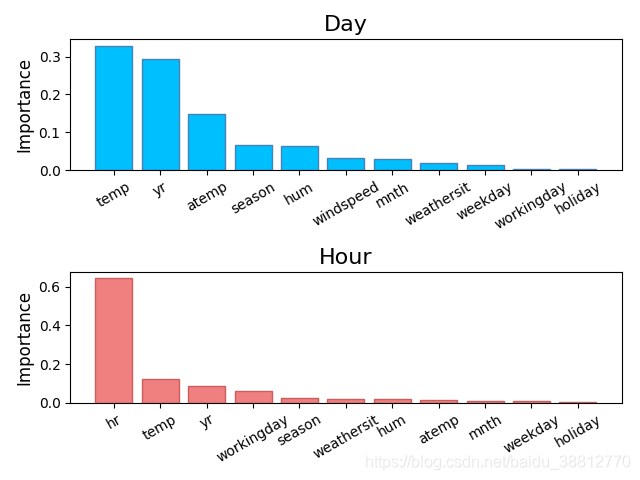
mp.subplot(211)
mp.title('Day', fontsize=16)
mp.ylabel('Importance', fontsize=12)
sorted_indices = fi_dy.argsort()[::-1]
pos = np.arange(sorted_indices.size)
mp.bar(pos, fi_dy[sorted_indices], facecolor='deepskyblue', edgecolor='steelblue')
mp.xticks(pos, day_headers[sorted_indices], rotation=30)

mp.subplot(212)
mp.title('Hour', fontsize=16)
mp.ylabel('Importance', fontsize=12)
sorted_indices = fi_hr.argsort()[::-1]
pos = np.arange(sorted_indices.size)
mp.bar(pos, fi_hr[sorted_indices], facecolor='lightcoral', edgecolor='indianred')
mp.xticks(pos, hour_headers[sorted_indices], rotation=30)

mp.tight_layout()
mp.show()