Codeforces1195D2-Submarine in the Rybinsk Sea (hard edition)-优快云博客

本文深入探讨了一种针对数字位数匹配的算法实现，通过枚举和计算不同位数数字间的贡献，有效解决了特定数学问题。算法利用了位运算、数组和函数调用等技术，实现了高效的数据处理。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

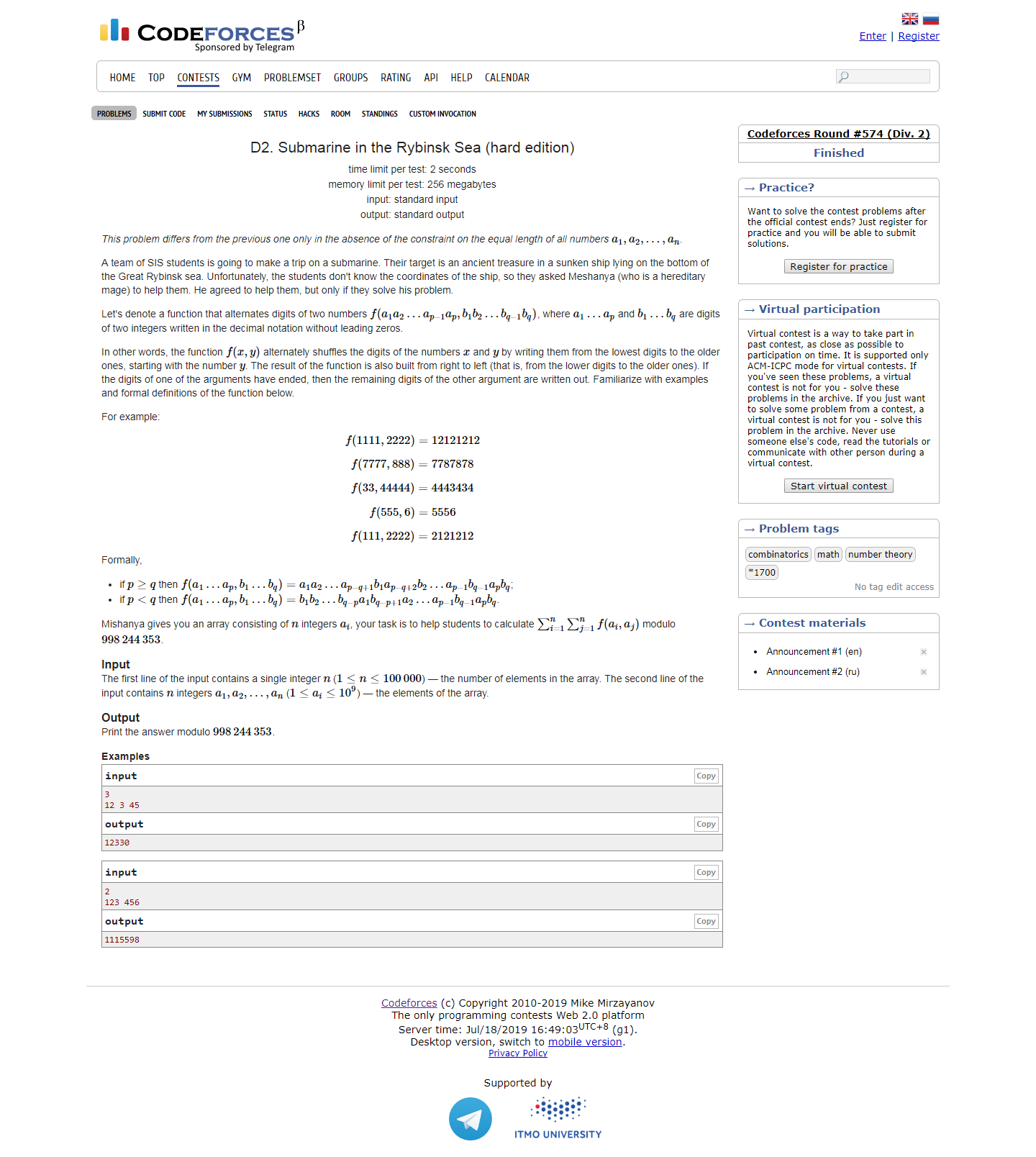
题意很简单。

可以看出，每一个数最多只有$10$位。而只要位数相同，数字不同的话对另一个数没有影响。

对于每一个数$x$，考虑其为函数的前一个数时对答案造成的影响，枚举函数的后一个数的位数$y$，按题意计算贡献，放入$a[x][y]$中。

同理，若$x$是函数的后一个数，可计算出贡献放入$b[x][y]$中。

再用一个$sum[i]$数组表示位数为$i$的数有几个。

最后再枚举每一个数$i$和位数$j$，$ans+=(a[i][j]+b[i][j])*sum[j]$

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N=1e5+5,mod=998244353;
 4 int n;
 5 long long a[N][10],b[N][10],sum[N];
 6 long long power(int k)
 7 {
 8     long long ans=1;
 9     for(int i=1;i<=k;i++)ans=(ans*10)%mod;
10     return ans;
11 }
12 int main()
13 {
14     scanf("%d",&n);
15     for(int i=1;i<=n;i++)
16     {
17         int x;
18         scanf("%d",&x);
19         long long k1=0,k2=0;int t=0;
20         for(int j=1;j<=10;j++)
21         {
22             long long p=x%10;
23             x/=10;
24             if(!x&&!t)t=j;
25             k1=(k1+p*power(j*2-2))%mod;
26             a[i][j]=(k1+x*power(j*2));
27             k2=(k2+p*power(j*2-1))%mod;
28             b[i][j]=(k2+x*power(j*2));
29         }
30         sum[t]++;
31     }
32     long long ans=0;
33     for(int i=1;i<=n;i++)
34         for(int j=1;j<=10;j++)
35             ans=(ans+(a[i][j]+b[i][j])*sum[j])%mod;
36     printf("%lld\n",ans);
37     return 0;
38 }