4.5 Splay Trees(伸展树)
Splay tree guarantees that any M consecutive tree operations starting from an empty tree take at most O(M logN). The guarantee does not preclude the possibility that any single operation might take O(N) time.
Generally, when a sequence of M operations has total worst-case running time of O(M F(N)), we say that the amortized running time is O(F(N)). Thus a splay tree has an O(logN) amortized cost per operation.
If any particular operation is allowed to have an O(N) worst-case time bound, and we still want an O(logN) amortized time bound, then it is clear that whenever a node is accessed, it must be moved.(Otherwise, we can keep Find this node)
The basic idea of splay tree is that after a node is accessed, it is pushed to the root by a series of AVL tree rotations. Splay tree do not require the maintenance of height or balance information.
4.5.2 Splaying
Zig Step: This step is done when p is the root. The tree is rotated on the edge betweenx andp. Zig steps exist to deal with the parity issue and will be done only as the last step in a splay operation and only whenx has odd depth at the beginning of the operation.

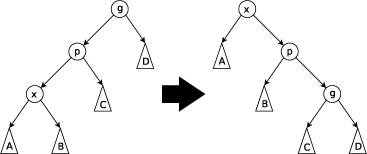
Zig-zig Step: This step is done when p is not the root andx andp are either both right children or are both left children. The picture below shows the case wherex andp are both left children. The tree is rotated on the edge joiningp withits parent g, then rotated on the edge joining x with p.
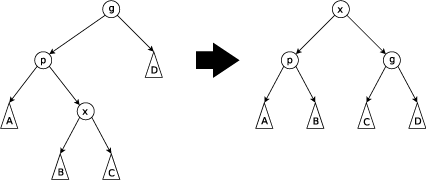
Zig-zag Step: This step is done when p is not the root andx is a right child andp is a left child or vice versa. The tree is rotated on the edge betweenx andp, then rotated on the edge between x and its new parentg.
Insertion
1. First insert the node as with a normal binary search tree.
2. Then splay the newly inserted node x to the top of the tree.
Deletion
Plan A:
Swap the value X with either the rightmost node of its left sub tree (its in-order predecessor) or the leftmost node of its right subtree (its in-order successor). Then we remove that node instead. In this way, deletion is reduced to the problem of removing a node with 0 or 1 children. Finally, we splay the parent of the removed node to the top of the tree.
Plan B:
The node to be deleted is first splayed then deleted. This leaves the tree with two sub trees. The maximum element of the left sub tree (: METHOD 1), or minimum of the right sub tree (: METHOD 2) is then splayed to the root. The right sub tree is made the right child of the resultant left sub tree (for METHOD 1). The root of left sub tree is the root of melded tree.
4.6 Tree Traversals (Revisited)
Because of the ordering information in a binary search tree, it is simple to list all the keys in sorted order.
inorder traversal(Routine to print a binary tree in order):
void PrintTree( Search T )
{
if( T != NULL )
{
PrintTree( T->Left );
PrintElement( T->Element );
PrintTree( T->Right );
}
}postorder traversal(Routine to compute the height of a tree):
int Height( Tree T )
{
if( T == NULL )
return -1;
else
return 1 + Max( Height(T->Left), Height(T->Right));
}




 本文详细介绍了伸展树(Splay Trees)的基本概念、操作流程及其应用特性,并对比了B树的相关知识点。通过本文,读者可以了解到伸展树如何通过一系列AVL树旋转将节点推到根位置,以及伸展树在插入、删除操作上的具体实现方法。同时,文章还探讨了B树的基础知识。
本文详细介绍了伸展树(Splay Trees)的基本概念、操作流程及其应用特性,并对比了B树的相关知识点。通过本文,读者可以了解到伸展树如何通过一系列AVL树旋转将节点推到根位置,以及伸展树在插入、删除操作上的具体实现方法。同时,文章还探讨了B树的基础知识。
















 7786
7786

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








