对糖尿病分类数据集进行特征降维和聚类
一、数据预处理+默认参数随机森林
# 忽略警告
import warnings
warnings.simplefilter('ignore')
# 数据处理
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler # 标准化
# 时间
import time
# 划分数据集
from sklearn.model_selection import train_test_split
# SMOTE过采样
from imblearn.over_sampling import SMOTE
# 模型和评估指标
from sklearn.ensemble import RandomForestClassifier # 随机森林模型
from sklearn.metrics import classification_report, confusion_matrix
1、数据预处理
dt = pd.read_csv(r'C:\Users\acstdm\Desktop\python60-days-challenge-master\项目 5-糖尿病分类问题\Diabetes .csv')
print('数据基本信息:')
print(dt.info())
# 数据清洗
dt['Gender'] = dt['Gender'].str.upper() # 统一性别为大写
dt['CLASS'] = dt['CLASS'].str.strip() # 去除类别空格
# 检查一下 处理好了
print(dt['CLASS'].unique())
print(dt['Gender'].unique())
# 离散特征编码
mapping = { # 定义映射矩阵
'Gender':{
'M':1,
'F':0
},
'CLASS':{
'N':0,
'P':1,
'Y':2
}
}
dt['Gender'] = dt['Gender'].map(mapping['Gender'])
dt['CLASS'] = dt['CLASS'].map(mapping['CLASS'])输出:
数据基本信息:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1000 entries, 0 to 999
Data columns (total 14 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 ID 1000 non-null int64
1 No_Pation 1000 non-null int64
2 Gender 1000 non-null object
3 AGE 1000 non-null int64
4 Urea 1000 non-null float64
5 Cr 1000 non-null int64
6 HbA1c 1000 non-null float64
7 Chol 1000 non-null float64
8 TG 1000 non-null float64
9 HDL 1000 non-null float64
10 LDL 1000 non-null float64
11 VLDL 1000 non-null float64
12 BMI 1000 non-null float64
13 CLASS 1000 non-null object
dtypes: float64(8), int64(4), object(2)
memory usage: 109.5+ KB
None
['N' 'P' 'Y']
['F' 'M']2、训练基准模型
# 划分数据集
X = dt.drop(['CLASS'], axis=1) # 特征
y = dt['CLASS'] # 标签
# 8:2划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# --- 1.默认参数随机森林模型 ---
print("--- 1.默认参数随机森林模型 ---")
start_time = time.time()
rf_model = RandomForestClassifier(random_state=42)
rf_model.fit(X_train, y_train)
rf_pred = rf_model.predict(X_test)
end_time = time.time()
print(f"随机森林模型训练时间:{end_time - start_time:.4f}, 秒")
print(f"默认随机森林分类报告:\n", classification_report(y_test, rf_pred))
print(f"默认随机森林混淆矩阵:\n", confusion_matrix(y_test, rf_pred))
print('*' * 55)输出:
--- 1.默认参数随机森林模型 ---
随机森林模型训练时间:0.1785, 秒
默认随机森林分类报告:
precision recall f1-score support
0 0.95 1.00 0.98 21
1 1.00 1.00 1.00 6
2 1.00 0.99 1.00 173
accuracy 0.99 200
macro avg 0.98 1.00 0.99 200
weighted avg 1.00 0.99 1.00 200
默认随机森林混淆矩阵:
[[ 21 0 0]
[ 0 6 0]
[ 1 0 172]]
*******************************************************二、主成分分析(PCA)进行特征降维
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler # 标准化
# 训练集和测试集已准备好
print("\n--- 2. PCA 降维 + 随机森林 (不使用 Pipeline) ---")
# 步骤 1:特征缩放
scaler = StandardScaler()
X_train_scaler = scaler.fit_transform(X_train)
X_test_scaler = scaler.transform(X_test)
# 步骤 2:PCA 降维
# 根据解释方差选择降到几维,例如保留95%的方差
pca_expl = PCA(random_state=42)
pca_expl.fit(X_train_scaler) # 在标准化后的训练集上拟合PCA模型
cumsum_variance = np.cumsum(pca_expl.explained_variance_ratio_) # 计算每个主成分的方差占比
n_components_to_keep_95_var = np.argmax(cumsum_variance >= 0.95) + 1 # 找出保留95%方差的最小主成分数
print(f"为了保留95的方差,需要的主成分数量:{n_components_to_keep_95_var}。")输出:
--- 2. PCA 降维 + 随机森林 (不使用 Pipeline) ---
为了保留95的方差,需要的主成分数量:12。使用降低到 9 维的效果:
n_components_pca = 9
pca_manual = PCA(n_components=n_components_pca, random_state=42) # 初始化PCA模型
X_train_pca = pca_manual.fit_transform(X_train_scaler) # 标准化后的训练集上拟合并转换PCA
X_test_pca = pca_manual.transform(X_test_scaler) # 标准化后的测试集进行PCA转换
print(f"PCA降维后训练集的形状:{X_train_pca.shape},测试集形状为:{X_test_pca.shape}。")
# 步骤 3:训练随机森林分类器
start_time_pca = time.time()
rf_model_pca = RandomForestClassifier(random_state=42)
rf_model_pca.fit(X_train_pca, y_train)
# 步骤 4:在测试集上预测
rf_pred_pca = rf_model_pca.predict(X_test_pca)
end_time_pca = time.time()
print(f"手动PCA降维后,训练与预测耗时:{end_time_pca - start_time_pca:.4f}秒")
print("手动PCA降维后,随机森林在测试集上的分类报告:")
print(classification_report(y_test, rf_pred_pca))
print("手动PCA降维后,随机森林在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, rf_pred_pca))输出:
PCA降维后训练集的形状:(800, 9),测试集形状为:(200, 9)。
手动PCA降维后,训练与预测耗时:0.2653秒
手动PCA降维后,随机森林在测试集上的分类报告:
precision recall f1-score support
0 0.70 0.76 0.73 21
1 0.00 0.00 0.00 6
2 0.95 0.98 0.97 173
accuracy 0.93 200
macro avg 0.55 0.58 0.56 200
weighted avg 0.90 0.93 0.91 200
手动PCA降维后,随机森林在测试集上的混淆矩阵:
[[ 16 0 5]
[ 3 0 3]
[ 4 0 169]]三、K-Means聚类
在降维的基础上进行聚类
from sklearn.preprocessing import StandardScaler
# KMeans聚类
from sklearn.cluster import KMeans
# 评估指标:轮廓系数、ch指数、db指数
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
# 画图
from matplotlib import pyplot as plt
import seaborn as sns
# 数据降维和可视化
from sklearn.decomposition import PCA
# 设置中文字体(解决中文显示问题)
plt.rcParams['font.sans-serif'] = ['SimHei'] # Windows系统常用黑体字体
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
# 标准化数据(聚类前通常需要进行标准化)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 评估不同k值下的指标
k_range = range(2, 11) # k从2-10
inertia_values = [] # 存储每个 k 值对应的 SSE
silhouette_scores = [] # 存储每个 k 值对应的 轮廓系数
ch_scores = [] # 存储每个 k 值对应的 ch系数
db_scores = [] # 存储每个 k 值对应的 db系数
for k in k_range:
kmeans = KMeans(n_clusters=k, random_state=42) # 初始化KMeans模型
kmeans_labels = kmeans.fit_predict(X_scaled) # 训练模型并获取聚类标签
inertia_values.append(kmeans.inertia_) # 计算存储每个k值的惯性(肘部法则)
silhouette = silhouette_score(X_scaled, kmeans_labels) # 轮廓系数
silhouette_scores.append(silhouette)
ch = calinski_harabasz_score(X_scaled, kmeans_labels) # ch指数
ch_scores.append(ch)
db = davies_bouldin_score(X_scaled, kmeans_labels) # db指数
db_scores.append(db)
# 绘制评估指标图
plt.figure(figsize=(12, 8))
plt.subplot(2, 2, 1)
plt.plot(k_range, inertia_values, marker='o')
plt.title("肘部法则确定最优聚类数 k (惯性,越小越好)")
plt.xlabel("聚类数 k")
plt.ylabel("惯性")
plt.grid(True) # 显示网格线,方便观察
plt.subplot(2, 2, 2)
plt.plot(k_range, silhouette_scores, marker='o', color='red')
plt.title("轮廓系数确定最优聚类数 k (越大越好)")
plt.xlabel("聚类数 k")
plt.ylabel("轮廓系数")
plt.grid(True)
plt.subplot(2, 2, 3)
plt.plot(k_range, ch_scores, marker='o', color='green')
plt.title("ch指数确定最优聚类数 k (越大越好)")
plt.xlabel("聚类数 k")
plt.ylabel("ch指数")
plt.grid(True)
plt.subplot(2, 2, 4)
plt.plot(k_range, db_scores, marker='o', color='blue')
plt.title("db指数确定最优聚类数 k (越小越好)")
plt.xlabel("聚类数 k")
plt.ylabel("db指数")
plt.grid(True)
plt.tight_layout()
plt.show()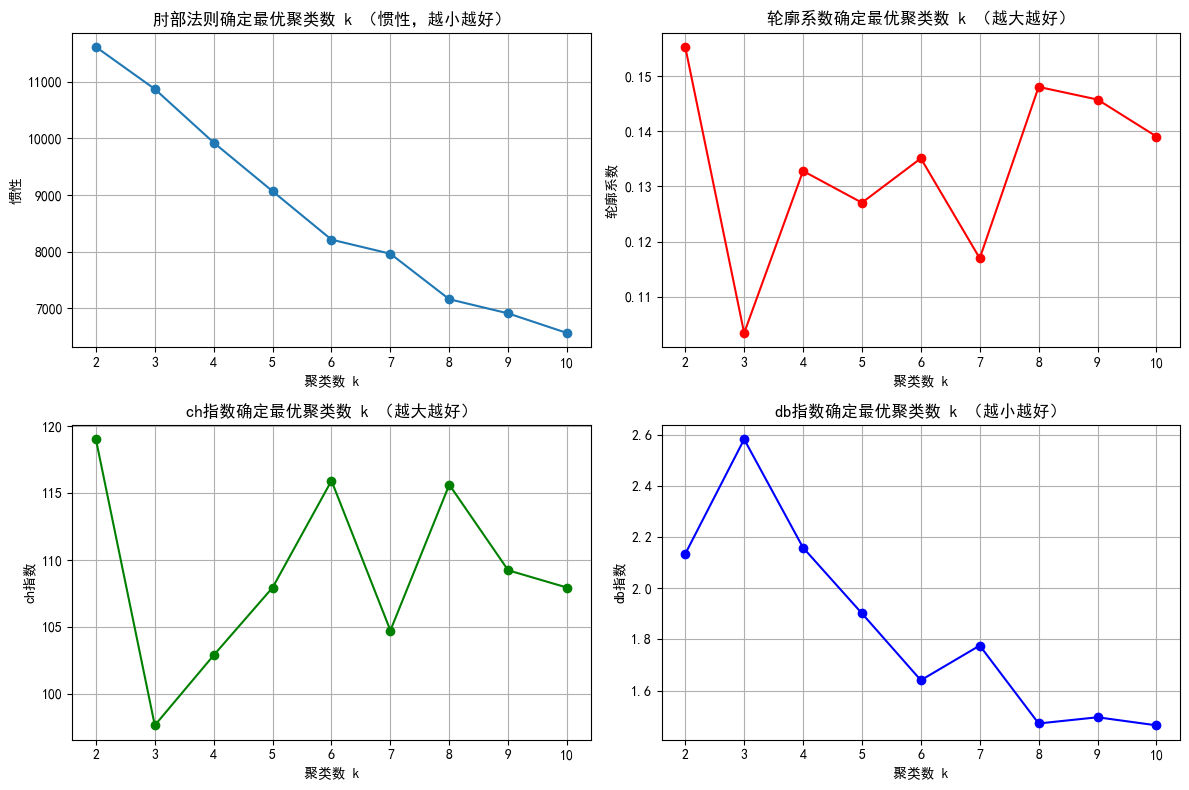
结合4个图像,选择局部最优的点,选择 8 比较合适。
k=8 时进行聚类
# 提示用户选择看值
selected_k = 8
# 使用选择的k值进行KMeans聚类
kmeans = KMeans(n_clusters=selected_k,
random_state=42,
init='k-means++', # 改用更智能的初始化方式
n_init=50, # 增加初始化次数
max_iter=300, # 增加迭代次数
) # 初始化KMeans模型
kmeans_labels = kmeans.fit_predict(X_scaled) # 训练模型并获取聚类标签
X['KMeans_Cluster'] = kmeans_labels # 将聚类标签添加到原始数据中
# 使用PCA降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled) # 对标准化后的数据进行降维
# KMeans 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=kmeans_labels, palette='viridis')
plt.title(f'Kmeans Clustering with k={selected_k} PCA Visualization')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()
# 打印 KMeans 聚类标签前几行
print(X[['KMeans_Cluster']].value_counts())输出:
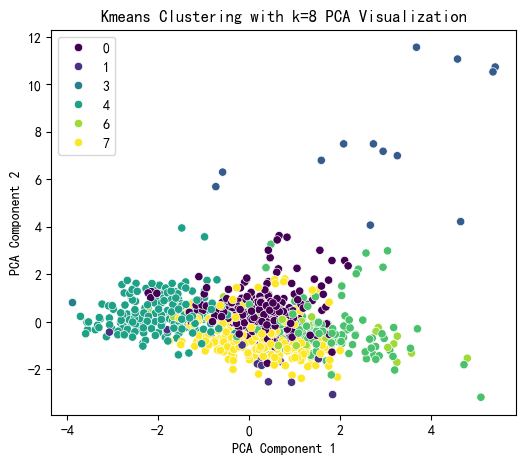
KMeans_Cluster
0 320
7 266
4 212
5 121
6 48
1 17
2 13
3 3
Name: count, dtype: int64




















 193
193

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








