二叉树

树的基本概念

定义

树是n（n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中有如下特点：

①有且仅有一个特定的、称为根（Root）的结点；

②当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、......、Tn，其中每一个集合本身又是一棵树，并且称为根的子树。

结点的度

结点拥有的子树数目称为结点的度

结点关系

结点子树的根结点为该结点的孩子结点。相应该结点称为孩子结点的双亲结点。

同一个双亲结点的孩子结点之间互称兄弟结点。

结点层次

从根开始定义起，根为第一层，根的孩子为第二层，以此类推。

树的深度

树中结点的最大层次数称为树的深度或高度

二叉树

二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。

 

说白了就是：结点的度最大为2

特点

二叉树有以下特点：

①每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。

②左子树和右子树是有顺序的，次序不能任意颠倒。

③即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。

性质

①在二叉树的第i层上最多有2^(i-1) 个节点。（i>=1）

推理过程：

第一层：最多1个节点

第二层：最多2个节点

第三层：最多4个节点

也就是说每一层节点（最多）数量就是上一层节点（最多）数据 * 2

作为等比数列可以看看：2^0 + 2^1 + 2^2 +  ....... + 2^(i-1)

根据等比数列的通项公式是：

，这里的q=2，a1=1，因此通项公式就是：2^(i-1)

 

②二叉树中如果深度为k,那么最多有(2^k)-1个节点。(k>=1）

推理过程：

等比求和：

当q≠1时，    或   

，这里推导一下：

由于q=2，因此Sn = - a1(1-2^k) = -a1 + 2^k = 2^k - a1 = 2^k - 1

 

③n0 = n2 + 1，n0表示度数为0的节点数，n2表示度数为2的节点数。

推理过程：

n0表示度数为0的节点，也就是n0表示没有子节点的节点，n2表示有左右2个子树的节点，那么，假如一颗tree的深度为k，那么第k层的最多节点数量应该是：2^(k-1) = 2^k / 2个，除去第k层，那么1-k-1层的节点数量最多是(2^（k-1）)-1 = 2^k / 2 - 1

n0节点数（单层）是：2^(k-1) = 2^k / 2

n2节点数（tree总和）是：(2^（k-1）)-1 = 2^k / 2 - 1，即n2 = n0 - 1，

转换过来就是：n0 = n2 + 1

 

④在完全二叉树中，具有n个节点的完全二叉树的最小深度为[log2n]+1，其中[log2n]是向下取整。

推理过程：

什么叫做完全二叉树，或者，完全二叉树定义是什么？

答：①该树非最后一层的结点都是满的；②最后一层的叶结点必须集中到左边。

通俗来讲就是：倒数第二层的结点必须有左结点。

那么深度为K的二叉树，其结点最多就是：(2^k)-1个节点

那么深度为K的完全二叉树，其第（K-1)层都是满的，因此（K-1）层总和就是：(2^(k-1))-1，假如第K层就1个节点，这就是该完全二叉树的最小深度了，就是：n = (2^(k-1))-1 + 1 = 2^(k-1)。

n=2^(k-1)，k-1 = log2N，k = log2N + 1，这里的最后1层只有一个节点的情况下推导出来的k = log2N + 1

 

⑤若对含 n 个节点的完全二叉树从上到下、从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：

(1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;

(2) 若 2i>n，则该结点无左孩子， 否则，编号为 2i 的结点为其左孩子结点；

(3) 若 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点。

推理过程：

本人目前2019年11月19日17:21:25能力有限，推导不出来

斜树

所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。

满二叉树

在一棵二叉树中。如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

满二叉树的特点有：

①叶子只能出现在最后一层。出现在其它层就不可能达成平衡。

②非叶子结点的度一定是2。

3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

（感觉可以左右对称了）

完全二叉树

对一颗具有n个结点的二叉树按层编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

特点：

①叶子结点只能出现在最后一层和倒数第2层。

②最下层的叶子结点集中在树的左部。

③倒数第二层若存在叶子结点，一定在右部连续位置。

④如果结点度为1，则该结点只有左孩子，即没有右子树。

⑤同样结点数目的二叉树，完全二叉树深度最小。

注：满二叉树一定是完全二叉树，但反过来不一定成立。

 

说白了就是除了最后一层，完全二叉树就是满二叉树。而最后一层的叶子节点集中在整个左侧树。

二叉树的存储结构

顺序存储

二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点，并且结点的存储位置，就是数组的下标索引。

说白了就是对二叉树从上到下、从左到右依次编号，编号正好对应一维数组的索引。

二叉链表

由二叉树定义可知，二叉树的每个结点最多有两个孩子。因此，可以将结点数据结构定义为一个数据和两个指针域。表示方式如图所示：

 

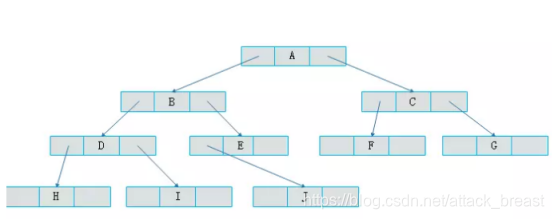
采用一种链表结构存储二叉树，这种链表称为二叉链表。

二叉树遍历

前，中，后序遍历只是指父节点遍历的顺序

前序遍历

父节点->左子树->右子树

对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。

中序遍历

左子树->父节点->右子树

对于树中的任意节点来说，先打印它的左子树，然后再打印它的本身，最后打印它的右子树。

后序遍历

左子树 -> 右子树 ->父节点

对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印它本身。

层序遍历

层次遍历就是按照树的层次自上而下的遍历二叉树

平衡二叉树

产生原因

二叉搜索树有一个缺点，在插入数据是有序的序列（包括升序和降序），会导致二叉树退化成链表，从而导致在查找，删除，添加时的性能均从O（logN）降低为O（N）

二叉排序树

定义：或者是一颗空树，或者是一颗具有如下性质的树：

1）若左子树不为空，那么左子树上面的所有节点的关键字值都比根节点的关键字值小

2）若右子树不为空，那么右子树上面的所有节点的关键字值都比根节点的关键字值大

3）左右子树都为二叉树

4）没有重复值，这个在实际操作中有点难度

特点

平衡二叉树本质上是特殊的二叉搜索树（二叉排序树），它具有二叉搜索树所有的特点，此外它有自己的特别的性质，如下：

①它是一棵空树或它的左右两个子树的高度差的绝对值不超过1；

②平衡二叉树的左右两个子树都是一棵平衡二叉树。

什么是平衡因子

平衡因子指的是，平衡二叉树在保持平衡的时候，是通过平衡因子来判断的。

节点的平衡因子 = 该节点的左子树的高度 - 该节点右子树的高度。

只有当值等于-1（右子树的高度大），0（左右子树的高度相等），1（左子树的高度大）的时候，能够代表该子树是平衡的除此之外，就认为该节点已经失衡了，需要旋转来维持平衡，

平衡二叉树的旋转分类

左旋转

右斜树向左旋转，升序适合左旋转

右旋转

左斜树向右旋转，降序适合右旋转

左右旋转

先左旋转，然后再右旋转

（右侧失衡，则先左后右旋转）

右左旋转

先右旋转，然后再左旋转

个人感想（不一定准确）

例如：右侧失衡，说明右面缺少树，鉴于右侧树任意节点均比父节点/根节点节点大，那怎么处理呢？

 

第一步：目前该树的父节点/根节点必须变成右子树，因为左子树所有节点都比目前父节点/根节点小，为了满足二叉排序树，必须把目前的父节点/根节点变成右子树，左子树某个节点变成未来的父节点/根节点。

 

第二步：如果想把父节点/根节点变成右子树，则必须把目前左子树变成降序排序，然后再以某个节点为圆心进行右旋

 

只有变成降序再去右旋，才能保证既是排序树，同时又是平衡二叉树。

B树

①每个节点最多有m个子节点；

②每个非叶节点（根除外）至少有[m / 2]个子节点；

③非叶子根节点至少有两个子节点；

④一个包含k个子节点的父节点包含（k-1）个密钥；

⑤所有叶节点出现在同一层；