进行算法不可避免对于相关性能进行分析 ,小编也是简单学习到了关于时间复杂度的相关东西,所以进行内容判断!

可爱的小狗!表达了对于知识的渴望!二哈也是我最喜欢的宠物,在这里分享出来!
基本的概念
T(n)用来表达时#间复杂度的一个函数或者叫指标!计算算法运行不同的内容所需要的时间点总和。
一般而说,T(n) = Oh(n)
(H是在O中间的,这个地方不好进行书写 | 表示渐近时间)其中n为输入数据的多少
(没有具体的数量,只是进行定性进行分析。例如:较少,多,较多等具有模糊的概念。)
T(n)的值的大小表示具体的时钟周日期大小,这个地方的模糊概率,与具体的时钟没有关系
渐近基本概率
这个之中的Oh表示渐近符号

渐近符号
在计算时间分析的过程中,必须要利用渐近这个概念。所以必须要了解相关与渐近的符号以及其他的相关规律。 
标准记号和常用函数
基本的大学相关公式与相关的规律!
单调性
取整
取模
a modn = a - n [ a / n ]计算a取模之后的值
多项式

指数,对数,阶乘
基本的数学规律
近似公式
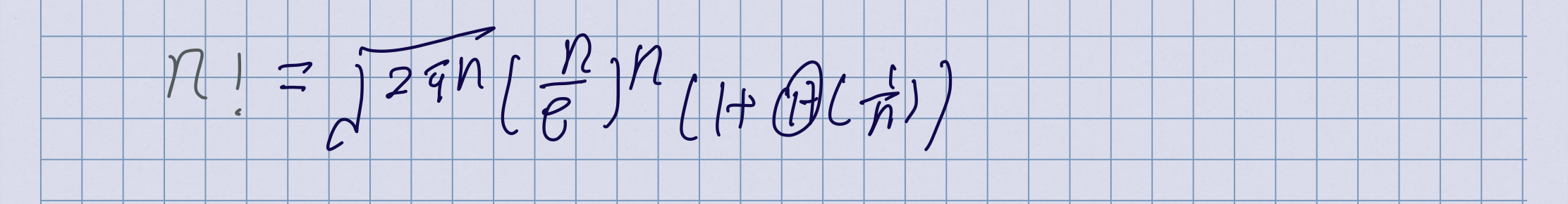
多重函数
经常用于递归式的相关的内容!
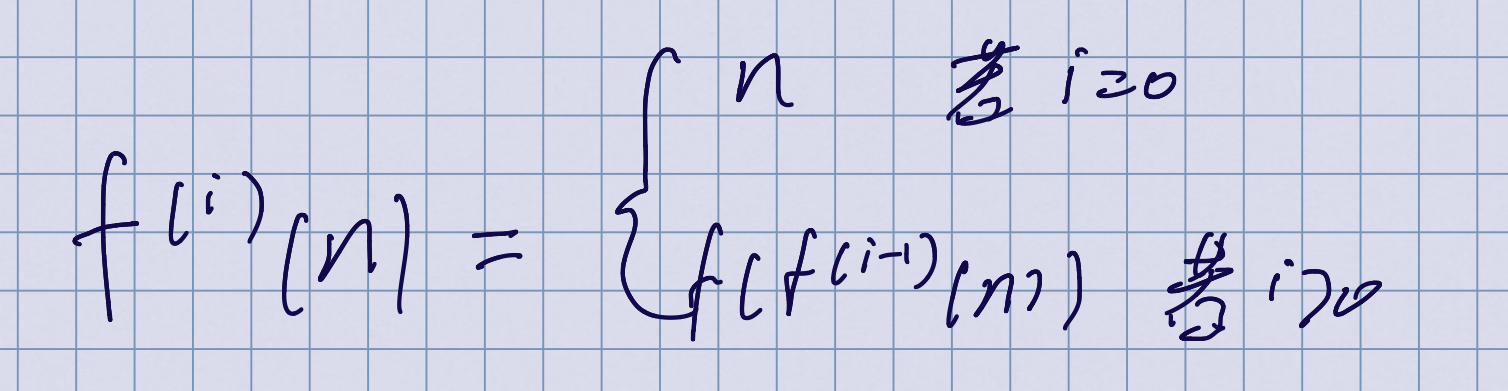
斐波那契数
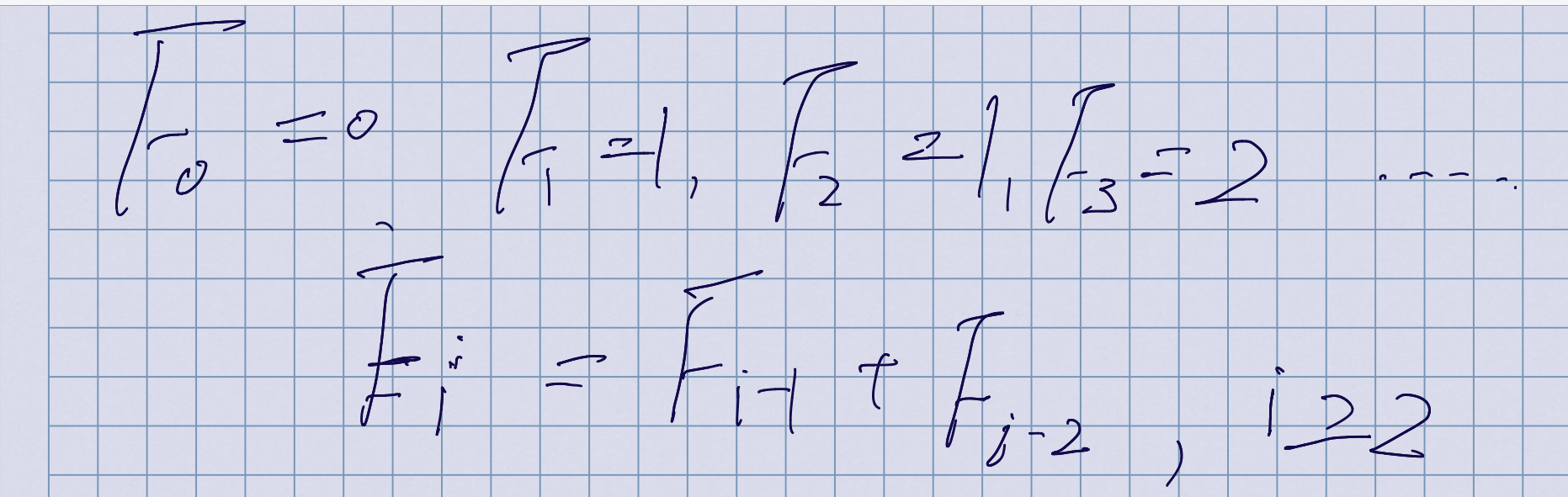





 本文介绍了算法分析中的时间复杂度,通过基本概念、渐近符号、标准记号和常用函数,深入探讨了算法性能。讲解了取整、取模、多项式、指数、对数、阶乘等数学概念,并触及了斐波那契数列。通过对这些基础知识的理解,读者可以更好地评估和优化算法效率。
本文介绍了算法分析中的时间复杂度,通过基本概念、渐近符号、标准记号和常用函数,深入探讨了算法性能。讲解了取整、取模、多项式、指数、对数、阶乘等数学概念,并触及了斐波那契数列。通过对这些基础知识的理解,读者可以更好地评估和优化算法效率。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








