Leetcode: 48. 旋转图像

因为不能使用另一个矩阵，所以想了一个自己原地旋转的算法。

对矩阵第一个元素分析该旋转方式，发现以下规律:

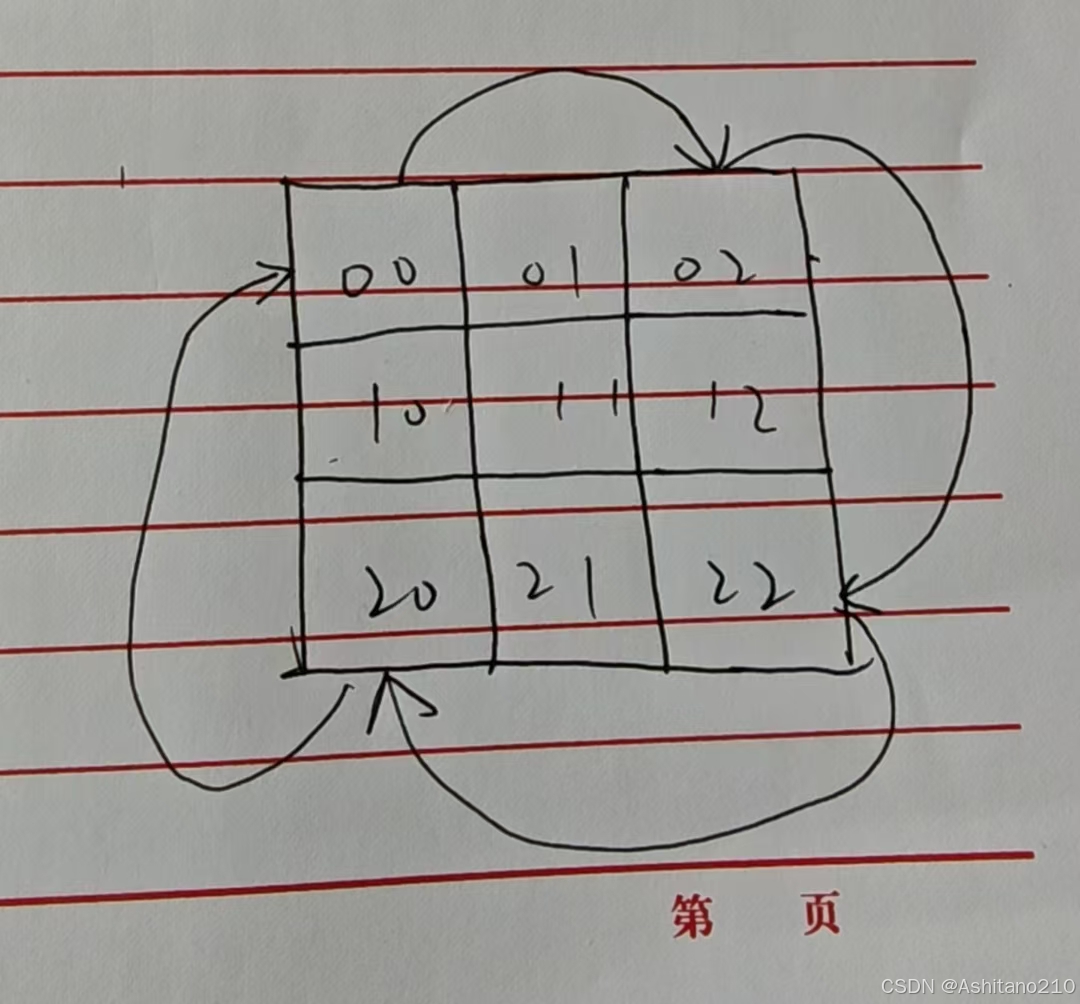
相当作4次交换操作，即一次大轮换。

因此该旋转其实就是对每一层矩阵(一层就是外面一圈)作一次旋转，也就是对一个n阶矩阵的旋转而言，只需要遍历第一排的n-1个元素，将他们按照下标规律做一次大轮换，然后再对内层矩阵做同样的操作。

以00->02->22->20->00为例，我们需要沿箭头向后交换，否则会导致将原值覆盖掉(比如令m[0][2]=m[0][0]，则当令m[2][2]=m[0][2]时用的是m[0][0]的值)。

这里我们将最上面的箭头叉掉不管，将m[0][0]的值保存在tmp中，向后赋值，即让箭头处的值等于箭尾处的值，设当前位置为m[j][k]，不难看出箭尾坐标为m[origin_matrix_size-1-k][j]，经过3次循环后，最后再将m[0][0]的值(现在在tmp里)赋值给m[0][2]。这样就完成了一层的旋转，接下来只需遍历第一排剩下的n-2个元素进行旋转，然后一直向内对内层矩阵进行同样操作直到内层矩阵大小<=1即可。

 (示意图）不过算法中是从外到内一层一层的转

代码如下:

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int origin_matrix_size = matrix.size();//原矩阵大小
        int cur_matrix_size = origin_matrix_size;//要旋转的矩阵大小
        int start = 0; //该轮轮转起始位置
        while (cur_matrix_size > 1) //矩阵大小=1时不需要旋转
        {
            simplyrot(start, origin_matrix_size, cur_matrix_size, matrix);
            ++start;
            cur_matrix_size -= 2; //内层矩阵大小-2(因为去除了一头一尾)
        }
    }
    
    void simplyrot(int start,int origin_matrix_size,int cur_matrix_size,vector<vector<int>>& matrix)
    {
        int tmp;//暂存
        for (int i = start; i < start + cur_matrix_size - 1; i++) 
        //最后一个元素不需要操作，会导致和第一个重复
        {
            int j = start, k = i; //该次循环的开始位置
            tmp = matrix[j][k];
            int count = 3;
            while (count-- > 0)
            {
                matrix[j][k] = matrix[origin_matrix_size-1-k][j]; 
                //向后旋转，否则会覆盖原本的值
                int t = j; 
                j = origin_matrix_size - 1 - k;
                k = t;
            }
            matrix[j][k] = tmp; 
        }
    }
    
};