dxf中凸度的计算

以前在做dxf文件解析的时候，对于凸度的处理采用了简单粗暴的方式。见我前面写的博客：https://blog.youkuaiyun.com/yishang44/article/details/80338533。简直是个繁琐的过程，而在实际的使用过程中，也碰到各种极端情况，代码的bug也暴露出来，比如，doule值的0值判断；极小值做分母造成误差等。简直是折磨的人欲仙欲死的。

后面在CAD中查找资料，碰到另一种凸度描述

我在CAD中画了个图，做了些小标识，如下：

根据凸度的描述，我们可以很简单的得出：凸度 W = 。根据圆中角度关系，圆弧的弧度为，且，（原因是圆心角是圆周角的2倍）。这个就是凸度的另外一种描述的了。

我们通过凸度计算的是圆弧的圆心和半径。

可以看到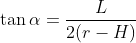 这里做个变换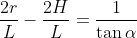

通过三角函数已知 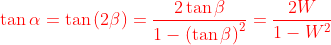                ………………①

                               

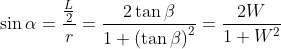
就可以得到 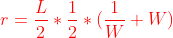         ………………………………………………………②                       

然后，就来求解圆心。自然第一反应是不是通过圆的标准公式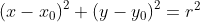 带入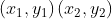和 r 求解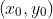。尝试之后太复杂了，实在不是个好办法。

这个时候就要转换下思路，这里就可以看出来，数学对于程序员的重要性了。

圆心可以通过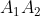线段上的点旋转90度实现。选择以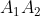的中点为旋转中心，（r-H）为半径的点B进行顺时针旋转来得到圆心O。

旋转变换公式，这个很多资料上都有写，这里就不推到了，直接上公式：

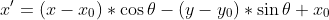
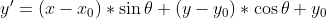
在本问题中θ= 90,公式可以简化成

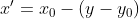
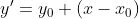
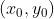为的坐标值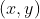，为B点坐标。求解B坐标可以用向量公式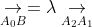，其中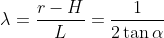

圆心为 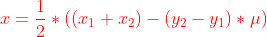     ………………………………………………③

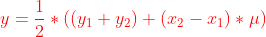                 ………………………………………………④

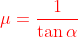                                                           ………………………………………………⑤

在CAD文档中明确说明了，W = 0的时候是直线。在计算过程中不会出现多次的判断问题了。把①⑤带入③和④中就可以直接得到圆弧的圆心了。计算简单方便。

顺便感概下，凸度的表示方法果然是神来之笔，赞美数学。