动态规划与背包问题

最新推荐文章于 2025-12-25 20:17:35 发布

原创最新推荐文章于 2025-12-25 20:17:35 发布 · 119 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法 #数据结构

本文通过两个实例介绍动态规划的应用：一是寻找从金字塔顶部到底部路径中节点和的最大值；二是解决01背包问题，即在限定背包容量的情况下选取物品组合以达到价值最大化。文章提供了完整的C++代码实现。

1、问题的出现
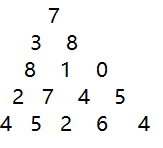
在这里插入图片描述
如上图这样一个金字塔,要求从第一层开始到最后一层，所经过的节点之和最大，其中一个节点只能从左下或者右下。
2、解决方式
1）动态规划
该方法首先定义了一个数组，用于储存最后一层节点。接着利用for循环将最后一层节点存储。然后，从最后一行依次遍历至第一行，从第一列遍历至第五列，最后选出所有节点之和最大的。
代码实现：

// 动态规划.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include<memory.h>

#define N 5

int Max(int &a, int &b)
{
	return a > b ? a : b;
}

int maxdigt[N + 1];
int MaxNum(int(*pArr)[N + 1])
{
	for (int i = 1; i <=N; i++)
	{
		maxdigt[i] = pArr[N][i];//保存第6行数据
	}

	for (int i = N-1; i >= 1; i--)//从第五开始，到第一行结束，从0起始
	{
		for (int j = 1; j <=i; j++)//第一列到第5列
		{
			maxdigt[j] = Max(maxdigt[j], maxdigt[j + 1]) + pArr[i][j];//最低层中2个中最大一个加上一层的数据
		}
	}
	return maxdigt[1];

}

int _tmain(int argc, _TCHAR* argv[])
{
	int arr[N + 1][N + 1] = {
		{0},
		{0,7},
		{0,3,8},
		{0,8,1,0},
		{0,2,7,4,5},
		{0,4,5,2,6,4}
	};
	memset(maxdigt, 0xff, sizeof(maxdigt));

	int max = MaxNum(arr);
	printf("%d\n", max);

	return 0;
}

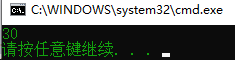
结果为：
在这里插入图片描述
3、利用动态规划的思想实现01背包问题
详细的说明

/*
问题阐述：
在给定的一组物品中，每种物品都有他的价值与重量。在设定背包的承受的重量下，怎么选择价值最大的？？？
*/

#include "stdafx.h"
#define MAXSUM 32

int Max(int a, int b)
{
	return a > b ? a : b;
}

int _tmain(int argc, _TCHAR* argv[])
{
	int amount = 5;//物品的个数
	int Weight = 20;//背包能承受最大的重量

	int W[] = { 0, 4, 8, 5, 12, 7 };//每个物品的重量
	int V[] = { 0, 7, 8, 6, 9, 10 };//每个物品的价值

	int f[MAXSUM][MAXSUM] = { 0 };

	for (int i = 1; i <= amount; i++)//
	{
		for (int j = 1; j <= Weight; j++)//重量
		{
			if (j<W[i])//加入当前物品后超出总的重量了，也就是装不下了
			{
				f[i][j] = f[i - 1][j];//说明没有选择第i个东西，这就是为什么数组第一个元素是0的原因
			}
			else//装的下
			{
				//在没有选择i商品与选择i商品(有可能选择了该商品也达不到最优价值)做出最好的选择
				f[i][j] = Max(f[i - 1][j], f[i - 1][j - W[i]] + V[i]);
			}
		}
	}

	printf("%d\n", f[amount][Weight]);
	return 0;
}