平衡二叉树(AVL)

1、概述
详细的说明
需要说明的是二种重要的旋转方式：
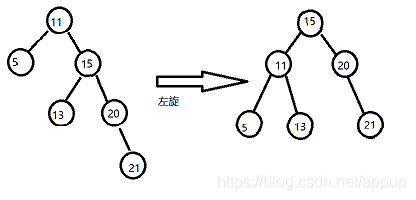
左旋：旧的根节点为新的根节点的左子树
新的根节点的左子树为旧的根节点的右子树
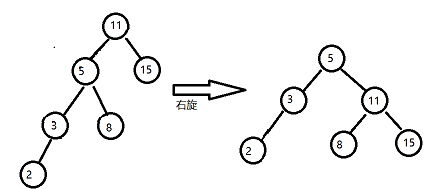
右旋：旧的根节点为新的根节点的右子树
新的根节点的右子树为旧的根节点的左子树
重点说明四种失衡二叉树的解决方式：
1）左左
当根节的左子树的左孩子添加了新的节点，导致二叉树为失衡二叉树。解决方式：

2）右右
当根节点的右子树的右孩子加入新节点导致二叉树失衡。解决方式：

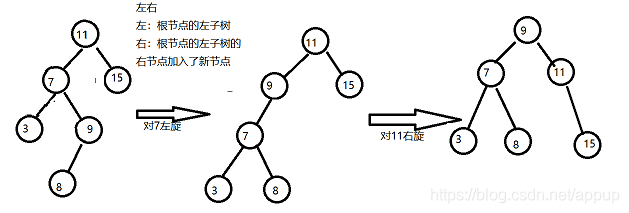
3）左右
当根节的左孩子的右子节点加入新的节点，导致二叉树失衡。解决方式：对根节的左子树进行左旋，然后对根节点进行右旋。

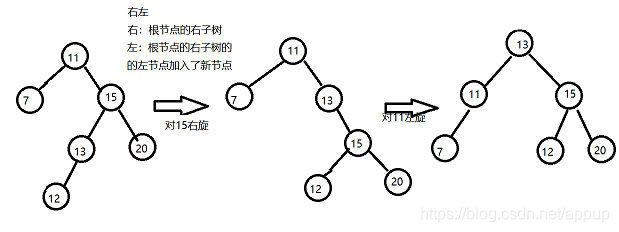
4）右左
当根节点的右孩子的左子节点加入新的节点，导师二叉树失衡。
解决方式：对根节点的右子树进行右旋，接着对根节点进行左旋。

2、程序实现
1）.cpp文件

#include "stdafx.h"
#include"AVLTree.h"

int _tmain(int argc, _TCHAR* argv[])
{
	AvlTree<int>tree;
	tree.InsertNode(11);
	tree.InsertNode(7);
	tree.InsertNode(15);
	tree.InsertNode(3);
	tree.InsertNode(9);

	tree.InsertNode(8);
	return 0;
}

2）.h文件用于具体的实现

#include<iostream>
#include<memory.h>

int Max(int a, int b)
{
	if (a>b)
	{
		return a;
	}
	return b;
}

template<class T>
class AvlTree
{
	struct TreeNode //节点
	{
		T data;//数据
		int height;//高度
		TreeNode* pleftChild;//左子树
		TreeNode* prightChild;//右子树
	};
public:
	AvlTree()
	{
		pRoot = 0;
	}
	void InsertNode(const T&insertData);//插入节点
private:
	TreeNode* pRoot;//根节点
	void _InsertNode(TreeNode**pNode, const T&insertData);
	int height(TreeNode* pNode);//计算树的高度

	void Rotateleft(TreeNode** pNode);//左旋
	void Rotateright(TreeNode** pNode);//右旋
	void RotateLeftRight(TreeNode** pNode);
	void RotateRightLeft(TreeNode** pNode);
};

template<class T>
int AvlTree<T>::height(TreeNode*pNode)
{
	if (pNode)
	{
		return pNode->height;
	}
	return -1;
}

template<class T>
void AvlTree<T>::InsertNode(const T&insertData)
{
	_InsertNode(&(pRoot), insertData);
}

template<class T>
void AvlTree<T>::_InsertNode(TreeNode**pNode, const T& insertData)
{
	TreeNode* root = *pNode;

	if (!root)
	{
		TreeNode* pNewNode = new TreeNode;
		memset(pNewNode, 0x00, sizeof(TreeNode));
		pNewNode->data = insertData;

		*pNode = pNewNode;
	}
	else
	{
		if (insertData>root->data)//插入值比当前节点的数据大
		{
			_InsertNode(&(root->pleftChild), insertData);//在该节点的左子树上

			if (height(root->prightChild) - height(root->pleftChild)>=2)//此时成为失衡二叉树
			{
				if (insertData>root->pleftChild->data)//插入节点的数据大于最底下一个左子树的数
				{
					Rotateleft(&root);//左旋转
				}
				else
				{
					RotateRightLeft(&root);//右左旋
				}
				*pNode = root;
			}
		}
		if (insertData < root->data)//插入值比当前节点的数据小
		{
			_InsertNode(&(root->pleftChild), insertData);
			if (height(root->prightChild) - height(root->pleftChild) >= 2)//失衡
			{
				if (insertData<root->pleftChild->data)
				{
					Rotateright(&root);//右旋
				}
				else
				{
					RotateLeftRight(&root);//左右旋
				}
				*pNode = root;
			}
		}
	}
	(*pNode)->height = Max(height((*pNode)->pleftChild), height((*pNode)->prightChild)) + 1;
}

//左旋转：旧的根节点作为新的根节点的左子树
       //新的根节点的左子树为旧根节点的右子树
template<class T>
void AvlTree<T>::Rotateleft(TreeNode** pNode)
{
	TreeNode* pRoot = *pNode;
	TreeNode* pTemp = pRoot;//将原来的根节点保存在临时的节点中

	pRoot = pRoot->prightChild;//新的根节点右子树为新的根节点
	pTemp->prightChild = pRoot->pleftChild;//新的根节点的左子树为旧的根节点的右子树
	pRoot->pleftChild = pTemp;//旧的根节点为新根节点的左子树

	*pNode = pRoot;

	pTemp->height = Max(height(pTemp->pleftChild), height(pTemp->prightChild)) + 1;//重新计算旋转之后的节点
	pRoot->height = Max(height(pTemp->pleftChild), height(pTemp->prightChild)) + 1;
}

//右旋转：旧的根节点作为新的根节点的右子树
//新的根节点的右子树为旧根节点的左子树
template<class T>
void AvlTree<T>::Rotateright(TreeNode** pNode)
{
	TreeNode* pRoot = *pNode;
	TreeNode* pTemp = pRoot;//将原来的根节点保存在临时的节点中

	pRoot = pRoot->pleftChild;//新的根节点右子树为新的根节点
	pTemp->pleftChild = pRoot->prightChild;//新的根节点的右子树为旧的根节点的左子树
	pRoot->prightChild = pTemp;//旧的根节点为新根节点的右子树

	*pNode = pRoot;

	pTemp->height = Max(height(pTemp->pleftChild), height(pTemp->prightChild)) + 1;
	pRoot->height = Max(height(pTemp->pleftChild), height(pTemp->prightChild)) + 1;
}

template<class T>
void AvlTree<T>::RotateLeftRight(TreeNode** pNode)
{
	Rotateleft(&((*pNode)->pleftChild));
	Rotateright(pNode);
}

template<class T>
void AvlTree<T>::RotateRightLeft(TreeNode** pNode)
{
	Rotateright(&((*pNode)->prightChild));
	Rotateleft(pNode);
}