字符串的模式匹配：kmp算法

引言

这一次我们来讲解kmp算法，这是一种更高效的算法，但是很多人就会疑问了，这个算法还是比较困难的你能讲好？面对你们的这些疑问，我只能说

初步分析

对于字符串的模式匹配BF算法我已经在我之前的文章中细致的讨论过了
BF算法
但是BF算法效率太低了，有没有更好的算法能够提高效率呢？我们思考一下，在BF算法中对于每一次匹配失败时我们做了什么样的操作，我们在主串S中从某一个字符$$\begin{gathered} C_x=D_0(匹配成功) \\ {C}_{x+1}=D_1(匹配成功) \\ ...... \\ {C}_{x+n}\ne D_n(匹配失败) \end{gathered}$$
此时我们发现以$C_x$为首的连续m个字符与T串并不相同，也就是没有匹配上，但是我们怎么样来进行判断下一个呢？我们选择从$C_{x+1}$开始来进行与T串的比较，等一下，等一下，你发现没有，假设上一次匹配失败时假设发生在$C_{x+n}\ne D_n(匹配失败,且n>1)$那么其实$C_{x+1}$是已经跟$D_1$比较过的对吧，如$D_1\ne D_0$那么肯定的存在$D_0\ne C_{x+1}$对吧，也就是说如果我们提前知道$D_1$与$D_0$的关系的话，我们其实是可以进行跳过以$C_{x+1}$为首的字符串的比对的，我们知道的是D_1与D_0都是串T中的一部分，所以我们是可以提前知道$D_1$与$D_0$的关系的，同理的话就可以跳过$C_{x+1}、C_{x+2}、.....$，假如说现在$C_{x+k}=D_0(k<n)$，那么我们看一下从$C_{x+k}$开始的字符串有和字符串T相同的可能吗？假设从$C_{x+k}$开始的字符串与T串相等了，那么必然有$$\begin{gathered} C_{x+k}=D_0 \\ {C}_{x+k+1}=D_1 \\ {C}_{x+k+2}=D_2 \\ ..... \\ {C}_{x+n-1}=D_{n-k-1} \end{gathered}$$但是我们前面已经得知的是：
$$\begin{gathered} C_x=D_0 \\ {C}_{x+1}=D_1 \\ {C}_{x+2}=D_2 \\ ..... \\ {C}_{x+n-1}=D_{n-1} \end{gathered}$$
也就是说如果要是从$C_{x+k}$开始的串可以与T串匹配上至少要有：
$$\begin{gathered} D_0=D_k \\ {D}_1=D_{k+1} \\ ...... \\ {D}_{n-k-1}=D_{n-1} \end{gathered}$$
也就是说如果T串满足上面的式子才可能与以$C_{x+k}$为首的字符串进行匹配，而上面的式子又说明T串的这种性质与仅T串本身有关，也就是说我们要先在T串中查找这种性质。
我们继续上面的分析，如果满足上面的公式的话我们继续比较$D_{n-k}$与$C_{x+n}$就行了，也就是说我们直接根据已经比较过的原有信息筛选了一大批的不可能的子串，同时因为$C_{x+k}=D_1$这一个k值的变化是从1向n值逐渐增大的，一旦遇到$C_{x+k}$使得接下来的字符组成的子串满足上面的公式的话，那么$[C_{x+k},C_{x+n-1}]$这一个子串是能够满足上述公式的最长子串，同时这一个子串使得$[C_{x+k},C_{x+n-1}]=[D_0,D_{n-k-1}]=[D_k,D_{n-1}]$成立，那么现在问题就转换为了如何去寻找字符$D_n$之前的前n-k个字符组成的串使得其与$D_0$包括$D_0$在内的n-k个连续字符组成的串相等而且这个串要尽可能的长的问题，如果在字符$D_n$处找到了这样一个串，我们只需要将T串的位置跳转到$D_{n-k}$的位置进行比较其与$C_{x+n}$的值即可这样我们就能继续进行比较了，但是如果在T串中不存在这样的一个字符串使得上述公式成立的话，说明我们要进行$D_0$与$C_{x+n}$进行比较了，如果还不相同说明，我们需要进行比较下一个字符$C_{x+n+1}$，如此进行下去，我们依然可以判断出，到底T串与S串是否能够匹配上。
通过上面的分析，我们发现在一段已经进行匹配过的部分虽然匹配失败了，但是其仍能帮我们排除一部分不可能的情况，而且这种性质与T串本身的组成有关，我们通过上面的分析知道了在匹配失败之后，可以将T串的位置跳转至$D_{n-k}$继续将其与原字符串中的$C_{x+n}$继续比较，可以看出S串中的位置是不需要变的，只需要将T串跳至$D_{n-k}$的位置可以看出T串要跳转的位置与两个值有关一个是$k$一个是$n$,其中$n$表示的是匹配失败的字符的在T串中的数组下标（即在第n+1个字符匹配失败），$k$表示的是在T串中从第$k+1$个字符开始T串中的字符与T串首部开始的字符重复了（这是重复字符子串开始的下标），n-k是不是表示的是这一个重复的字符串的长度，因为字符串$[D_0,D_{n-k-1}]$共有$n-k$个字符，所以T串中的字符匹配失败后，需要跳转的位置是由这一个在T串中重复的字符串的长度决定的。根据这两个指标我们就可以得到在T串中位置x出的字符匹配失败后，需要跳转到的位置，然后在此位置继续进行比较。也就是说T串中的每一个字符都对应了这样的一个需要进行跳转的值，所以我们要有一个新的数组来存储匹配失败之后需要跳转至的位置的下标，即next数组（如果你想的话，也可以将这一个数组称呼为其他的名字，这无所谓，但是next这一名字还是比较形象的）。
虽然我们现在已经了解了kmp算法的思想，有了next数组之后匹配就好进行了，但是我们现在又遇到了新的问题，next数组怎么计算？

进一步分析

next数组的计算

假设我们是在T串的第一个位置进行比较时失败了，而第一个字符前面是没有其他的字符的也就不存在一个满足上面性质的T串的子串，也就是说k值是不存在的对吧，因为数组下标不可能比0还小，但是这是T串中的第一个字符，因为T串中的第一个字符已经与当前S串的字符不相同的，所以S串中的字符移动到下一个，将S串的下一个字符与T串中的第一个字符进行比较对吧，但是k值无法确定这是不行的，所以我们要为其赋一个特殊值，使得其可以计算，而且这一个特殊值不能干扰判定，我们思考一下假如为k值赋0的话会不会影响判定，如果将前面不存在这样一个串的k值按照0来推算，那么就会出现这种情况，n-k=0，也就是跳转到下标0的位置，但是下标为0的地方就是刚才比较过的地方，显然如果仍然跳转至下标为0的地方就会出现，不停的发生这种跳转，显然字符串的匹配会卡到这个地方，如图所示：

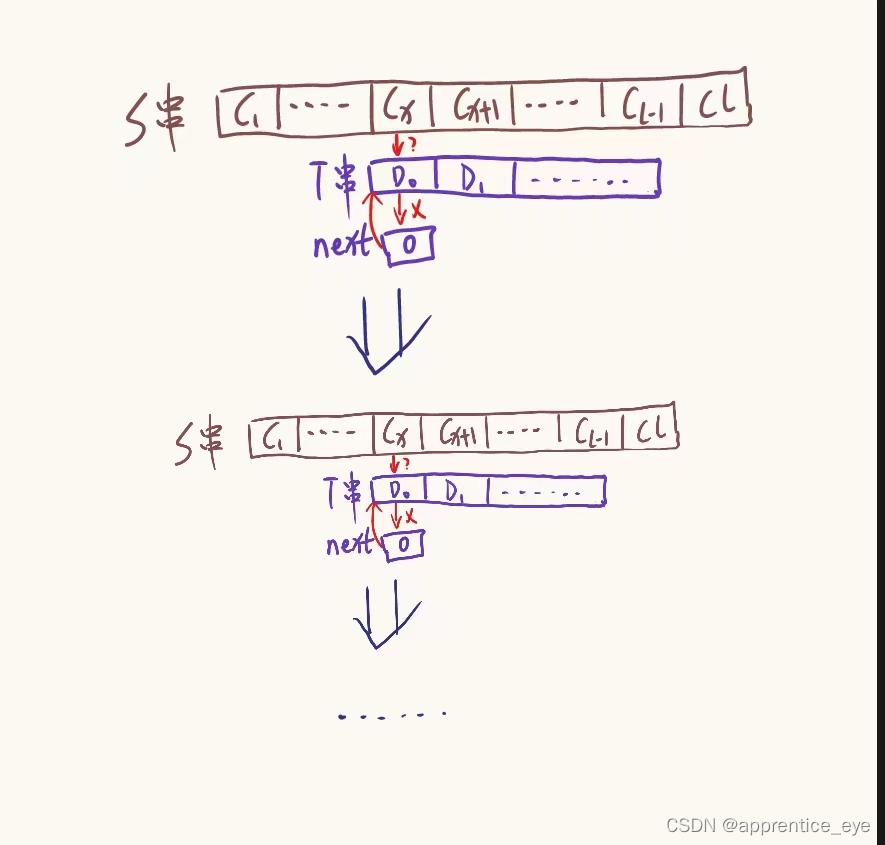
我们对于这种情况显然不能接受，但是选用其他的数字的话又会出现其他的情况，难办，那么怎么办呢？我先卖个关子。
上面我们讨论了在第一个字符处匹配失败的情况，虽然上面留下了一个小问题，我们先不去解决，先考虑如果在第二个字符处匹配失败呢？
T串中的第一个字符的这种情况比较好判断，但是我们进一步分析一下，如果是T串中的第二个字符$D_1$的话，我们发现第二个字符$D_1$的前一个字符就是$D_0$而$D_0=D_0$，所以k值应为0，因为此时比较的是第二个字符所以n-k=1，由此，若在T串中的第二个字符的位置发生比较错误，应将T串中的字符跳转到$D_1$,然后从此位置继续与S串中比较失败的字符进行比较，但是显然跳转到$D_1$仍然会出现上面在第一个字符处匹配失败会出现的问题。
但是第三个位置呢?第三个位置字符$D_2$前面是不是有两个字符$D_1、D_0$，其中$D_0=D_1或D_0\ne D_1$我们先来讨论$D_0\ne D_1$也就是对于这种情况是不是存在下面的这种情况：
如果求子串的话，在$D_2$字符前面只存在一种满足我们之前说的公式的串即：
$$\begin{gathered} D_0=D_0 \\ {D}_1=D_1 \end{gathered}$$
此时我们因为$D_0\ne D_1$所以我们需要将$D_0$与S串中现在比较的位置进行比较对吧。对此，我们很容易理解，但是当$D_0=D_1$时是什么情况？我们经过简单分析，我们就能很容易的发现对于当$D_0=D_1$时存在下面两种情况：
$$\begin{gathered} 第一种情况考虑： \\ {D}_0=D_0 \\ {D}_1=D_1 \\ 第二种情况考虑： \\ {D}_2=D_1 \end{gathered}$$
我们看下，假如真的存在第二种情况成立，那么显然也存在第一种情况成立，对吗？那么此时我们应该按照哪一种情况进行字符串T的跳转，第一种还是第二种？我们分析一下，假设按照第一种的方式进行跳转，此时应该将字符串T跳转到$D_0$对吧，但是跳转至$D_0$的话，我们是不是就默认的跳过了这样一种可能匹配上的情况，这样给你说你可能不太明白，让我来给你画一幅图示，这样你就能很明白了。

我们再思考一下好像对于T串中任意一个字符$D_x$都存在$$\begin{gathered} D_0=D_0 \\ {D}_1=D_1 \\ ...... \\ {D}_{x-1}=D_{x-1} \end{gathered}$$对吧，显然不能这样跳转，因为同样的按照上面的方法进行分析的话可能会跳过一些可能匹配上的情况，也就是说我们所寻找的这样一个在T串中的串不能是$D_x$字符之前所有字符组成的最长串。我们前面又论证了这一个串要尽可能的长对吧，那么我们要寻找的是一个什么样的串呢？显然对此我们有了明显的答案，我们要寻找的是字符$D_x$之前除了$[D_0,D_{x-1}]$之外的最长串对吧。如果到现在你们听懂了的话，我们看一下我们讨论的第二个字符匹配失败的情况是不是就不能按照原来的分析了，既然我们排除了$[D_0,D_{x-1}]$显然如果第二个字符匹配失败的话，其前面除了这个串之外没有其他字符串了，所以我们是不是也要将其跳转至$D_0$处进行比较，如果跳转后比较失败是不是发生了在第一个字符$D_0$匹配失败的情况了，这样我们肯定会遇到我们上面分析的那种问题，也就是陷入了在这种匹配的循环之中。
我们现在思考一下，我们现在的主要问题有next数组的计算问题与$D_0$匹配失败next[0]的计算以及之后如何跳转的问题。现在我们依然不去想后一个问题，我们继续进行分析next数组的计算问题。
上面我们看出在第三个字符匹配失败之后，next数组的计算就已经有点复杂了，如果在第四个字符或者第五个字符匹配失败next数组的计算更加复杂，我们心中不禁升起这样一个疑问，虽然如果next数组计算出来之后会使得模式匹配的效率提高，但是next数组计算的过程好像更耗时间？同学们不要疑惑，下面请跟着我的思路继续走。
我们看一下假设我们计算出来了next[x]之后，我们要计算next[x+1]的话，既然next[x]已经出来了是不是说明前面在$D_x$之前的最长的重复的子串已经确定了，即一定存在下面的关系：
$$\begin{gathered} D_0=D_{x-next[x]} \\ {D}_1=D_{x-next[x]+1} \\ {D}_2=D_{x-next[x]+2} \\ ...... \\ {D}_{next[x]-1}=D_{x-1} \end{gathered}$$
而$D_{x+1}$之前的字符是不是比在$D_{x-1}$之前的字符多了一个$D_x$，其实前面的一些字符我们已经在求next[x]时已经计算过前面的一些字符是否相等了，所以我们就只需要证明$D_{next[x]}、D_x$是否相等就行了，如果相等的话，说明$next[x+1]=next[x]+1$，如图所示

如果不相等说明我们应该前面最大的公共子串长度为0？你觉的对吗？对？不对？我现在告诉你不对，因为我们上面只是说了：
$$\begin{gathered} D_0=D_{x-next[x]} \\ {D}_1=D_{x-next[x]+1} \\ {D}_2=D_{x-next[x]+2} \\ ...... \\ {D}_{next[x]-1}=D_{x-1} \\ {D}_{next[x]}\ne D_x \end{gathered}$$
但是我们有谈到过$D_0\ne D_{x-next[x]+1}、$$D_1\ne D_{x-next[x]+2}$$......$这些吗？那么有没有一种可能是这样的：
$$\begin{gathered} D_0=D_{x-next[x]+1} \\ {D}_1=D_{x-next[x]+2} \\ {D}_2=D_{x-next[x]+3} \\ ...... \\ {D}_{next[x]-1}=D_x \end{gathered}$$
那么这样$next[x+1]$是不是就等于$next[x]$了，那么有没有情况是这样的：
$$\begin{gathered} D_0=D_{x-next[x]+2} \\ {D}_1=D_{x-next[x]+3} \\ {D}_2=D_{x-next[x]+4} \\ ...... \\ {D}_{next[x]-2}=D_x \end{gathered}$$
这种情况是不是$next[x+1]=next[x]-1$了，这些可能很多，情况似乎又复杂起来了，我们得思考一下在这种情况下如何求解next数组了。
既然$D_x\ne D_{next[x]}$那我们就先向前比较$D_x、D_{next[x]-1}$的关系

1. 如果相等了那么这一个$[D_0,D_{next[x]-1}]$是可能与$[D_{x-next[x]+1},D_x]$匹配上的对吧，所以我们就只需要再进行比对$D_{x-1}、D_{next[x]-2}$的关系，依次类推直到$D_{x-next[x]+1}=D_0$,这就说明$next[x+1]=next[x]$对吧。
2. 如果不相等是不是需要再向前比较$D_x、D_{next[x]-2}$的关系，如果相等了就重复1.中的步骤,不相等就再进行2.中的操作，每进行一次2.中的操作，next[x+1]的值相较于前一次的值就会减1.
3. 重复上述操作就能得到一个next[x+1]，因为我们求此子串是从较长时向较短时求取的，所以目前得到的next[x-1]一定是最长的公共子串。

这样我们就能求取next[x+1]了对吧。至于有没有更简单的求解next数组的方法，这一个请大家发挥自己的聪明才智自由探索，如果你能找到更好的方法，那么请将你所知道的更好的方法告诉我。
我们现在已经解决了next数组的求值问题，但是我们还需要解决的问题是$D_0$匹配失败next[0]的计算以及之后如何跳转的问题。

对于特殊位置T串串首位置的next[0]的取值问题分析

前面我们说过对于$D_0$的next[0]的值具体赋一个什么样的值，我们感觉到了疑惑，前面我们假设了对其进行赋值为0，后面我们又讨论了如何求解next数组，显然对于其中的某一个next[i]，显然next[i]可能等于0，而对于之前的假设$next[0]=0$,我们已经分析出了结果，需要将S串中的字符移动到当前比较的字符的下一个，对于T串则需要移动到串首进行比较，而对于$next[i]=0(i\ne 0)$我们需要将T串移动到串首，而S串不需要进行任何操作，这两种操作是不同的，所以如果我们要使得$next[0]=0$的话，我们在进行判断的时候需要额外进行一次判断$next[i]=0$是不是出现在串首，如果我们不让$next[0]=0$的话，我们就需要让$next[0]$等于一个后面不可能出现的值，显然后面不可能出现负值，而-1是负值中比较特殊的，所以我们也可以选择-1作为next[0]的值。当然这并不是说next[0]不能等于后面的next数组可能出现的值，在这种情况下需要做额外的判断，不太方便。

好了，我们今天对于KMP算法的分析到此为止，如果你觉得本篇文章对你有用的话，请动一动手指帮博主点一个赞，你的支持就是我更新的动力。

结语

我是apprentice_eye，一个致力于让知识变的易懂的博主

小伙伴们，点个关注再走吧！！！