Numpy - 数组运算

1 场景

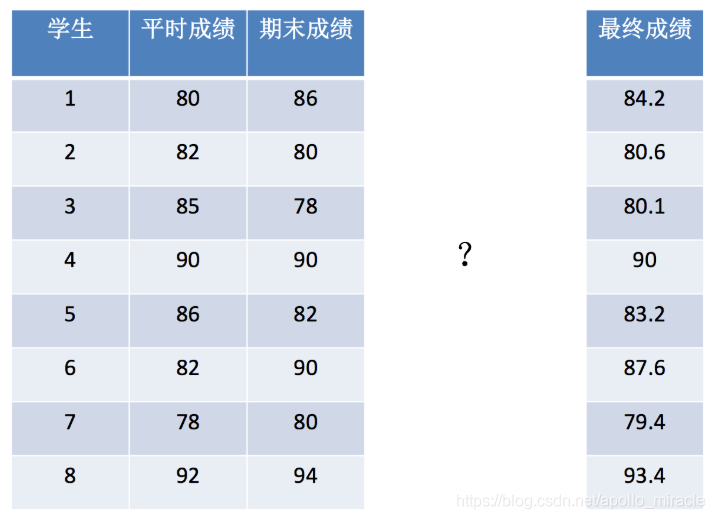
数据：

[[80,86],
[82,80],
[85,78],
[90,90],
[86,82],
[82,90],
[78,80],
[92,94]]

2 数组与数的运算

import numpy as np

arr = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
print(arr + 1)
"""
[[2 3 4 3 2 5]
 [6 7 2 3 4 2]]
"""
print(arr / 2)
"""
[[0.5 1.  1.5 1.  0.5 2. ]
 [2.5 3.  0.5 1.  1.5 0.5]]
"""

# 可以对比python列表的运算，看出区别
a = [1, 2, 3, 4, 5]
print(a * 2)
# [1, 2, 3, 4, 5, 1, 2, 3, 4, 5]

3 数组与数组的运算-广播机制

执行 broadcast 的前提在于，两个 ndarray 执行的是 element-wise的运算，而不是矩阵乘法的运算，矩阵乘法运算时需要维度之间严格匹配。Broadcast机制的功能是为了方便不同形状的array（numpy库的核心数据结构）进行数学运算

当操作两个数组时，numpy会逐个比较它们的shape（构成的元组tuple），只有在满足下述情况中的一种，两个数组才能够进行数组与数组

• 维度相等
• shape（其中相对应的一个地方为1）

例如：

Image (3d array):  256 x 256 x 3
Scale (1d array):              3
Result (3d array): 256 x 256 x 3

A      (4d array):  9 x 1 x 7 x 1
B      (3d array):      8 x 1 x 5
Result (4d array):  9 x 8 x 7 x 5

A      (2d array):  5 x 4
B      (1d array):      1
Result (2d array):  5 x 4

A      (2d array):  15 x 3 x 5
B      (1d array):  15 x 1 x 1
Result (2d array):  15 x 3 x 5

如果是下面这样，则不匹配：

A  (1d array): 10 x 2
B  (1d array): 12
A  (2d array):      2 x 1
B  (3d array):  8 x 4 x 3

这样就可以运算了：

In [16]: arr1 = np.array([[1,2,3,2,1,4], [5,6,1,2,3,1]])
    ...: arr2 = np.array([[1], [3]])

In [17]: arr1 * arr2
Out[17]: 
array([[ 1,  2,  3,  2,  1,  4],
       [15, 18,  3,  6,  9,  3]])

4 矩阵运算

如何能够达到我们想要的效果，直接得出每个学生的成绩！！！！这是机器学习最常见的问题之一，如何进行数据运算？

4.1 什么是矩阵

矩阵，英文matrix，和array的区别矩阵必须是2维的，但是array可以是多维的。

• np.mat() 将数组转换成矩阵类型

In [21]: a = np.array([[80, 86], [82, 80], [85, 78], [90, 90], [86, 82], [82, 90], [78, 80], [92, 94]])
    ...: np.mat(a)
Out[21]: 
matrix([[80, 86],
        [82, 80],
        [85, 78],
        [90, 90],
        [86, 82],
        [82, 90],
        [78, 80],
        [92, 94]])

4.2 矩阵乘法运算

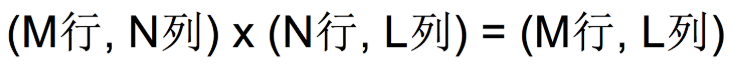
必须符合上面的式子，否则运算出错。

在进行矩阵运算的时候，可以直接使用一个乘法运算API

• mp.matmul

a = np.array([[80, 86],
              [82, 80],
              [85, 78],
              [90, 90],
              [86, 82],
              [82, 90],
              [78, 80],
              [92, 94]])
b = np.array([[0.7], [0.3]])

c = np.matmul(a, b)
print(c)
"""
[[81.8]
 [81.4]
 [82.9]
 [90. ]
 [84.8]
 [84.4]
 [78.6]
 [92.6]]
"""

4.3 矩阵应用场景

大部分机器学习算法需要用到