火柴排队（归并，逆序对）

最新推荐文章于 2024-03-07 22:52:11 发布

转载最新推荐文章于 2024-03-07 22:52:11 发布 · 102 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/MyNameIsPc/p/9075504.html

火柴排队（归并，逆序对）

给出数组a和b，每个数组有n个数，问如何重排列，使得\(\sum(a_i-b_i)^2\)最大。

首先转换一下式子，发现\((a_i-b_i)^2=a_i^2+b_i^2-2a_ib_i\)，因此只要最小化\(a_ib_i\)即可。

有个好东西叫做排序不等式，他告诉我们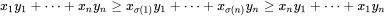
。因此我们只要将a和b都排个序就行了。剩下的工作就是求交换相邻两个数，最少几次能让两个序列相同序号的元素对齐。

如果把\(b_i\)跟着\(a_i\)排序，那么由于\(a_i\)已经变成了升序，序号是1,2,...,n，因此问题又转换成了要交换几步能将\(b_i\)排序。现在只要求\(b_i\)的逆序对就行了。注意必须保持b原有的顺序（至于为什么我也不知道啊qaq）。

#include <cstdio>
#include <algorithm>
#include <functional>
using namespace std;

typedef pair<int, int> pa;
const int maxn=1e5+5, mod=99999997;
int n, arr[maxn], tmp[maxn];
pa a[maxn], b[maxn];

int merge_sort(int *a, int beg, int end){
    if (beg+1==end) return 0;
    int mid=beg+end>>1, i=beg, j=mid, ans=0, cnt=beg;
    ans=merge_sort(a, beg, mid)+merge_sort(a, mid, end); ans%=mod;
    while (i<mid&&j<end){  //统计以j为后一个数的逆序对个数
        if (a[i]>a[j]) ans=(ans+mid-i)%mod, tmp[cnt++]=a[j++];  //为了避免i=mid,j=end必须else一下
        else tmp[cnt++]=a[i++];
    }
    while (i<mid) tmp[cnt++]=a[i++];
    while (j<end) tmp[cnt++]=a[j++];
    for (int i=beg; i<end; ++i) a[i]=tmp[i];
    return ans%mod;
}

int main(){
    scanf("%d", &n); int t;
    for (int i=0; i<n; ++i){ scanf("%d", &t); a[i]=make_pair(t, i); }
    for (int i=0; i<n; ++i){ scanf("%d", &t); b[i]=make_pair(t, i); }
    sort(a, a+n); sort(b, b+n);
    for (int i=0; i<n; ++i) arr[a[i].second]=b[i].second;
    printf("%d\n", merge_sort(arr, 0, n));
    return 0;
}

转载于:https://www.cnblogs.com/MyNameIsPc/p/9075504.html