基于ECC（椭圆曲线加密）与RSA的文件加密，算法C++实现

本文章来源于一次作业，提交于2019年6月，如果老师看到，请勿误认为作业抄袭

代码下载链接

https://download.youkuaiyun.com/download/anying0/11264650

软件基本功能介绍

ECC与RSA都是非对称加密算法，会生成不同的公钥和私钥，适合用于文件的加密传输与解密。因此，在此设计一个文件的加密解密系统。由于椭圆曲线需要选择一套复杂的参数，RSA中需要选取两个较大的质数，应该给予用户自定义这些加密参数的功能。考虑文件的加密解密过程难以验证其正确性，因此需要给ECC、RSA以及ECC-RSA串联系统都增设测试功能，可以对不同功能模块进行单元测试，验证算法的有效性。
综上所述，软件的主要功能定位为文件的ECC-RSA串联加密与解密。可选择功能为RSA算法与ECC算法的参数选择功能。附加测试功能为ECC算法、RSA算法以及ECC-RSA串联算法的单元测试功能。

软件设计

整体架构设计

本文设计的加解密系统通过一个流程控制程序来控制系统整体的流程，并完成与用户的交互，根据第一章节分析的需求以正确的逻辑形成功能。整个系统架构的流程设计如图1所示：

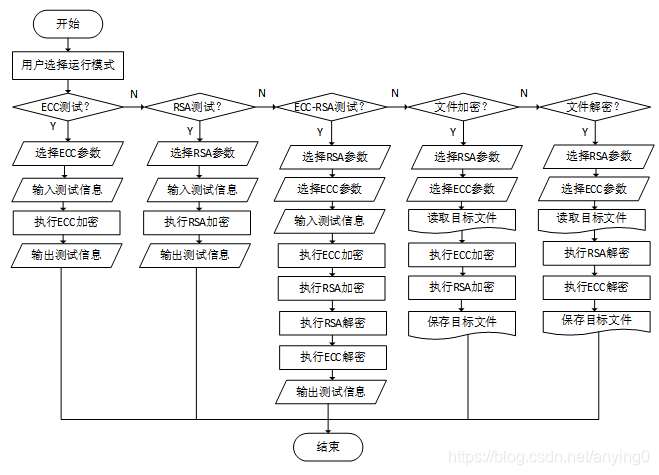
图1 非对称加解密系统框图
其中可以看到，系统架构从整体上分为五种运行模式，分别是ECC测试模式，RSA测试模式，ECC-RSA测试模型，文件加密模式以及文件解密模式。对于ECC测试模式、RSA测试模式以及ECC-RSA测试模式，程序流程是相似的，先设定加密算法的参数，再输入测试用例。程序对测试用例进行自动的先加密后解密，然后显示程序运行结果，从而判断算法的有效性。
对于文件加密流程，先输入加密算法的参数，然后读取需要加密的文件，利用ECC-RSA串联流程对文件进行加密，并且覆盖原文件。对于文件解密流程则正好相反，选择ECC-RSA的参数后，读取文件，进行RSA-ECC的串联流程解密，最终得到明文文件。

系统加密解密参数的设置流程

系统中关于选择RSA参数与ESA参数的部分，各自有两种模式。一种是直接使用系统的默认参数，好处为简单稳定，一定可以进行有效的加密。另一种是通过手动输入加密参数，加密参数需要自行验证后填入，如果填入错误的参数将无法进行正常的加密与解密。参数的设定思路以流程图表示。其中，RSA的参数设置如图2所示，ECC的参数设置流程如图3所示：

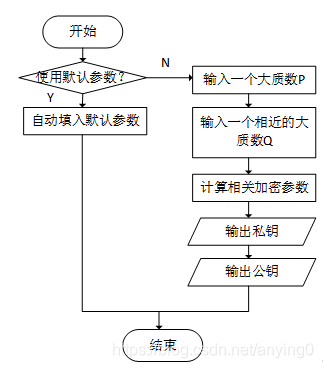
图2 RSA参数设置流程

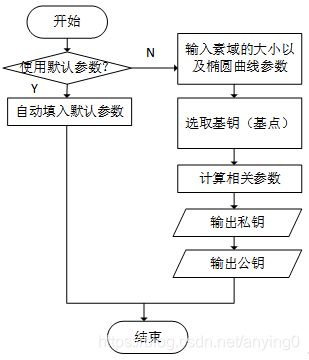
图3 ECC加密参数设置流程

ECC（椭圆曲线加密）的加密解密原理及其实现

ECC模块架构

ECC模型使用CPP封装成为一个类。ECC模型主要包含的功能有：设置ECC参数、计算私钥、计算公钥以及加密、解密。ECC模型可以调用的函数如下所示：

void setEllipticParameter(long long int kSet,long long int aSet,long long int bSet,long long int pSet,long long int rSet);
    //上方函数设置椭圆的相关参数，a与b为椭圆曲线y^2 = x ^ 3 +a*  x + b的参数。
    //p为一个素数是素域的范围，满足0<a<p,0<b<p,0<k<p,0<r<p
    //密文C1=r*A,密文C2也与r有关。
    //其中k相当于私钥信息
    //先选定素域x<p,曲线参数A与B，然后得到一个曲线上的基点A(x,y)，然后得到基点上的阶K,选择k<K，然后设置一个随机的r<k
    void calKey(long long int x,long long int y);//计算公钥，设置基钥A的坐标，B可以根据设置的私钥自动解算
    twopoint getPublicKey();//获取公钥，这个函数得到的是可以公开的秘钥
    void getPrivateKey(long long int &ko);//获取私钥
    long long int getP();//获取素域范围P
    void encode(char *in, char *out,long long int length,twopoint publicKey);//对字符串进行加密，长度参数为明文长度
    void decode(char *in,char *out,long long int length,long long int kKey);//对字符串进行解密，长度参数为密文长度

ECC加密解密原理

本文设计的ECC模型基于ElGamal公钥密码体制，所以下面着重进行ElGamal体制的算法描述：
1）设$p$为一个素数,$E$是有限素域$Z_p$上的椭圆曲线，$\alpha \in E$是椭圆曲线上的一个点，并且阶足够大，使得生成的离散对数问题是难解的。$p,E,\alpha$都是公开的。
2）随机选取整数$d(0<=d<ord(\alpha ))$，计算$\beta =d^{\alpha }$。其中$\beta$是公钥，$d$是私钥。
3）加密时，若明文为$X=(x_1,x_2)$，则密文$C=(c_1,c_2)$。选定随机整数$r,0<r\ast k<ord(\alpha )$，有$c_1=alpha\ast r$,$c_2=\alpha \ast k\ast r+X$。加密后密文内容是明文内容的两倍长。
4）解密时，$c_k.x=(c_1\ast K).x$，$c_k.y=p-(c_1\ast K).y$。原文$X=c_K+c_2$。
原理验证:$(X+\alpha \ast K\ast r)-d\cdot (\alpha \ast K)=(X+\alpha \ast K\ast r)-(\alpha \ast d)\ast K=m$
如果无法理解需要搜索椭圆曲线上计算相关的博客，推荐博客：https://blog.youkuaiyun.com/m0_37803704/article/details/79229738

ECC加密解密的函数实现

由于选用的是基于ElGamal体制的标准加密算法，加密核心函数说明如下：

twopoint ecc::ECodePoint(point m, twopoint publicKey)//Menezes-Vanstone的标准加密算法,用公钥A，B加密
{
    point c1,c2;
    c1 = mul(publicKey.first,r) ;
    point Y = mul(publicKey.second,r) ;
    c2 = add(m,Y);
return twopoint(c1,c2);
}

可以看到，对于一个明文m，可以加密为密文c1与c2.其中c1为公钥基钥在椭圆曲线空间上的r倍。C2为公钥在椭圆曲线上空间的r倍与明文点乘，在素域范围内取模的值。
相对应的，解密算法如下：

point ecc::DCodePoint(twopoint t, long long int kKey)//Menezes-Vanstone的标准解密算法，使用私钥k才可以解密
{
    point Z = mul(t.first,kKey);
    point c1k;
    c1k.x = Z.x;
    c1k.y = p-Z.y;
    point m;
    m = add(c1k,t.second);
return m;
}

ECC加密参数的搜索与验证

ECC椭圆曲线的参数筛选也是一个比较值得探讨的问题。在我们的程序中，固定在127为范围的素域的椭圆曲线上进行加密。在此基础上，搜寻具有一定数量的整数解的椭圆曲线的代码如下：

void findECC()
{
    int aMax,bMax,nMin;
    cout<<"素域范围必须为127，输入a的最大值:";
    cin>>aMax;
    cout<<"输入b的最大值:";
    cin>>bMax;
    cout<<"输入最少的整数解数量:";
    cin>>nMin;
    cout<<"可行的曲线:"<<endl;
    for(int a=5;a<aMax;a++)
        for(int b = 5;b<bMax;b++)
        {
            int n = 0;
            m1.setEllipticParameter(0,a,b,127,6);
            for(int x =1;x<127;x++)
            {
                int m = x*x*x+a*x+b;
                if(sqrt(m)-int(sqrt(m))<=0)
                {
                    n++;
                }
            }
            if(n > nMin)
            {
                cout<<"a:"<<a<<",b:"<<b<<",解的数量:"<<n<<endl;
            }
        }
}

使用枚举法来获取a和b在指定范围内的符合要求（至少有N个整数解）的椭圆曲线。然后针对这个椭圆曲线，可以搜寻其每个解作为基点的时候，对应的阶数，代码如下：

void findK()
{
    int a,b;
    cout<<"输入曲线的a:";
    cin>>a;
    cout<<"输入曲线的b:";
    cin>>b;
int n = 0;
m1.setEllipticParameter(0,a,b,127,7);
    for(int x =1;x<127;x++)
    {
        int m = x*x*x+a*x+b;
        if(sqrt(m)-int(sqrt(m))<=0)
        {
            cout<<"整数解:"<<x<<","<<sqrt(m)<<endl;
            int i;
            try{
                for(i=0;i<127;i++)
                {
                    point pp;
                    pp.x = x;
                    pp.y = sqrt(m);
                    m1.mul(pp,i);
                }
            }
            catch(...)
            {
                cout<<"阶数为："<<i+1<<endl;
            }
            n++;
        }
    }
}

在此程序中，如果阶数到达正确值，则会由于解为无穷远点，获得的值为可靠的解。为了阻止程序停止，可以使用程序内抛接异常的方式来进行获取。使用throw-try-catch的模式对值进行获取。

RSA 加密解密算法设计及实现

RSA模块设计

RSA模块也已类似的形式封装成一个类。由于ECC与RSA都为非对称加密算法，所以实际上的功能是雷同的，只是基础原理不同。RSA模块也是包含了，参数设定、公钥计算、私钥计算、加密、解密这五个板块的功能，如下所示：

    void calKey(long long int p,long long int q,long long int ei);//计算公钥和私钥，需要输入两个互质的质数p与q，以及一个满足e<(p-1)(q-1)的e
    void getPublicKey(long long int &eo);//得到公钥
    void getPrivateKey(long long int &dO);//得到私钥
    long long int getN();//得到p*q的值
    void encode(char *in,long long int *out,long long int length,long long int ei);//使用公钥加密, ci = mi^e（mod n）
    void decode(long long int *in,char *out,long long int length,long long int di);//使用私钥解密，mi = ci^d（mod n）

RSA 算法原理

1)找出两个相近的大素数$p,q$。
2）计算$N=p\ast q，\varphi (N)=(p-1)(q-1)$。
3)随机生成一个一个整数$e(1<e<\varphi (N))$。
4)求出$d$满足$((e\ast d)mod\varphi (N)=1)$，此时公钥为$(N,e)$，秘钥为$(N,d)$。
5)如果密文为$C$，明文为$M$，则加密过程为:$C=M^e(modN)$。
6)解密过程为$M=C^d(modN)$。

RSA加密解密算法实现

相比较于ECC，RSA的加密解密原理相对简单，无论是加密还是解密，都是通过解算方程：$a=b^c(modN)$实现的，在加密情况下：$C=M^e(modN)$，在解密情况下：$M=C^d(modN)$。方程求解的代码如下，其实就是穷举的：

long long int rsa::candp(long long int m, long long int b, long long int N)// = (m^b)%N
{
    long long int r=1;
    for(long long int i=0;i<b;i++)
    {
        r=r*m;
        r=r%N;
    }
    return r;
}

使用的是最简单的阶乘思路，为了避免过大的阶乘导致结果过大而无法进行有效计算，每轮迭代后都进行取模，从而限制了数据的膨胀。公钥与私钥的求取如下所示：

void rsa::calKey(long long int p, long long int q, long long int ei)
{
    e = ei;
    if(isRP(p,q))
    {
        N=p*q;
        long long int t=(p-1)*(q-1);  //求n的欧拉数
        d = 1;
        while(((e * d) % t) != 1)
        {
            d++;  //由公钥e求出私钥d
        }
    }
    else
    {
        cout<<"P与Q必须互质！"<<endl;
    }
}

其原理为在确认p与q后，若p与q互质（如果不互质则一定选错了参数），让N=pq ，t=(p-1)(q-1) 。找到一个d 使(e·d）%t==1 ，则d为私钥。

程序的测试与功能验证

ECC加密算法测试

在素域范围为127的前提下，从小到大依次选取多组椭圆曲线以及基点坐标进行加密算法测试。测试结果如下表所示：

序号	A	B	基点	K	R	正确加解密
1	15	9	(45,303)	17	7	是
2	37	26	(11,42)	11	6	是
3	73	78	(59,458)	13	9	是
4	488	484	(68,590)	11	9	是
5	1997	1726	(6,118)	11	6	是

可以看到，在限制素域范围的情况下，取各种椭圆曲线，都可以搜索出对应的基点以及阶数，并对K，R进行配置，最后顺利的对数据进行加密解密。由于计算机以及算法性能原因，素域范围限制在127。但是算法的有效性以及正确性已经得到了充分的验证。

RSA加密程序测试

不断地增大最初设置的P与Q，从而增大解算得到的秘钥，对RSA加密算法的可靠性进行验证。

序号	Q	P	E	D	正确加解密
1	1721	1723	13	1594837	是
2	2633	2647	17	6554609	是
3	3457	3461	13	9198277	是
4	7547	7549	17	43813237	是
5	15583	15601	23	84549287	是
6	31397	31469	43	597376803	是
7	60029	60091	71	2946630791	是

可以看到，当P和Q到达非常大的情况下，系统也可以正确的对信息进行加密解密运算。但是，当D达到10位数时，计算性能已经急剧下降，加密速率已经达到了每字符2分钟，因此无法进行更大数字的验证。在硬件条件允许的限制下，RSA算法的正确性得到了保证。

ECC-RSA串联加密测试

既然RSA与ECC算法的正确性得到了验证，其串联加解密也必然是正确的。下面只对功能性进行验证。RSA-ECC算法对26个英文字符以及10个数字字符的加密解密结果如下图所示。

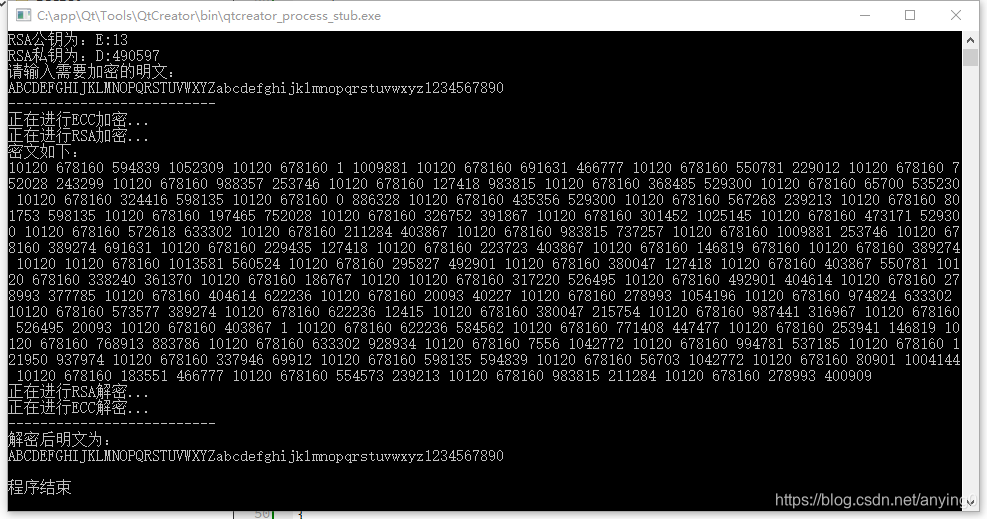
可以看出，系统可以对任意字符进行有效的加密以及解密。系统在默认参数的情况下进行实验，可以知道，ECC-RSA算法是正确有效的。

文件加密解密测试

文件的加密和解密功能将进行统一测试。首先准备一个测试文件tets,txt。如图所示：

然后利用程序对该文件进行加密，加密后的文件变为：

加密程序的界面显示了加密后的密文：

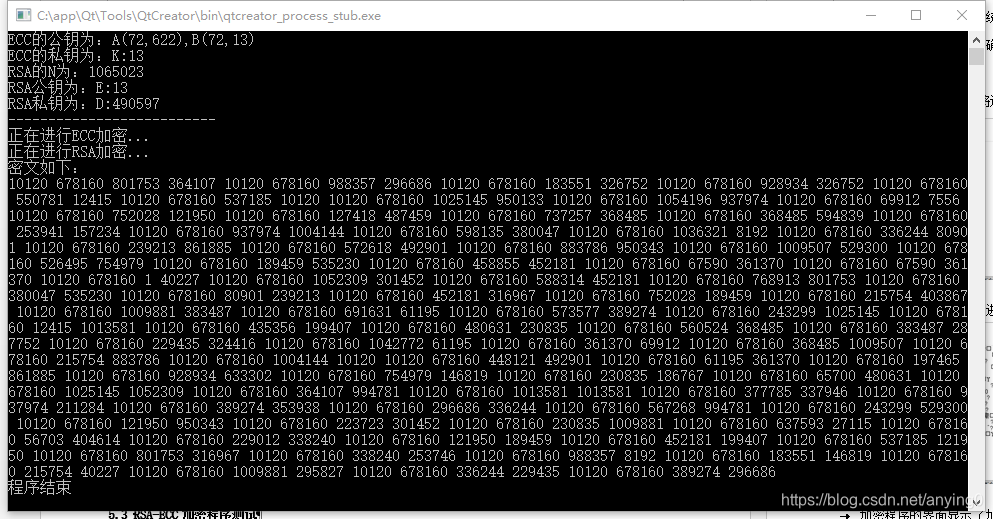
然后对文件进行解密，解密过程中程序显示如下：

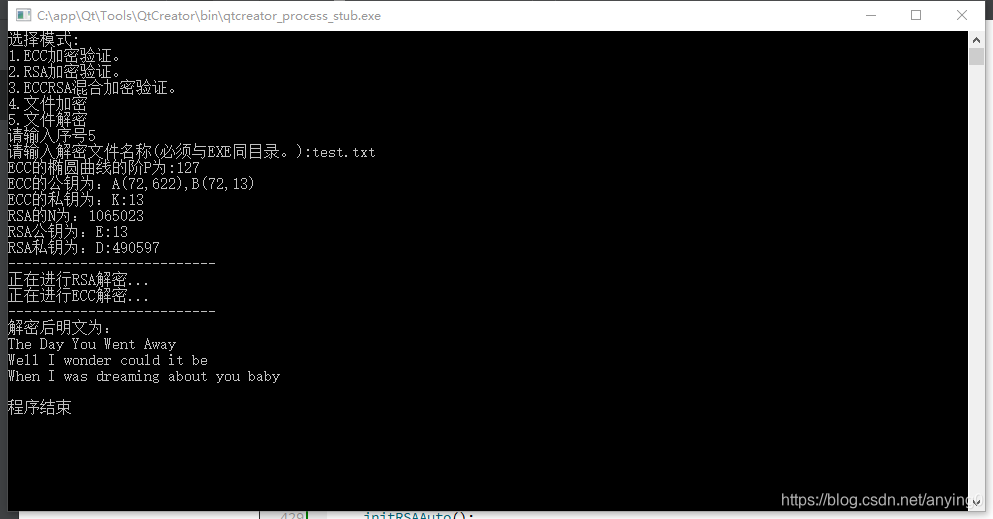
那么，原文件打开后内容为：

可以看到系统加密再解密后的文件与原文件完全相同，验证了加密功能与解密功能的实用性。对限制长度的文本文件可以进行加密与解密。

如果有帮助请点个赞谢谢