春招冲刺百题计划|动态规划

Java基础复习

1. Java数组的声明与初始化
2. Java ArrayList
3. Java HashMap

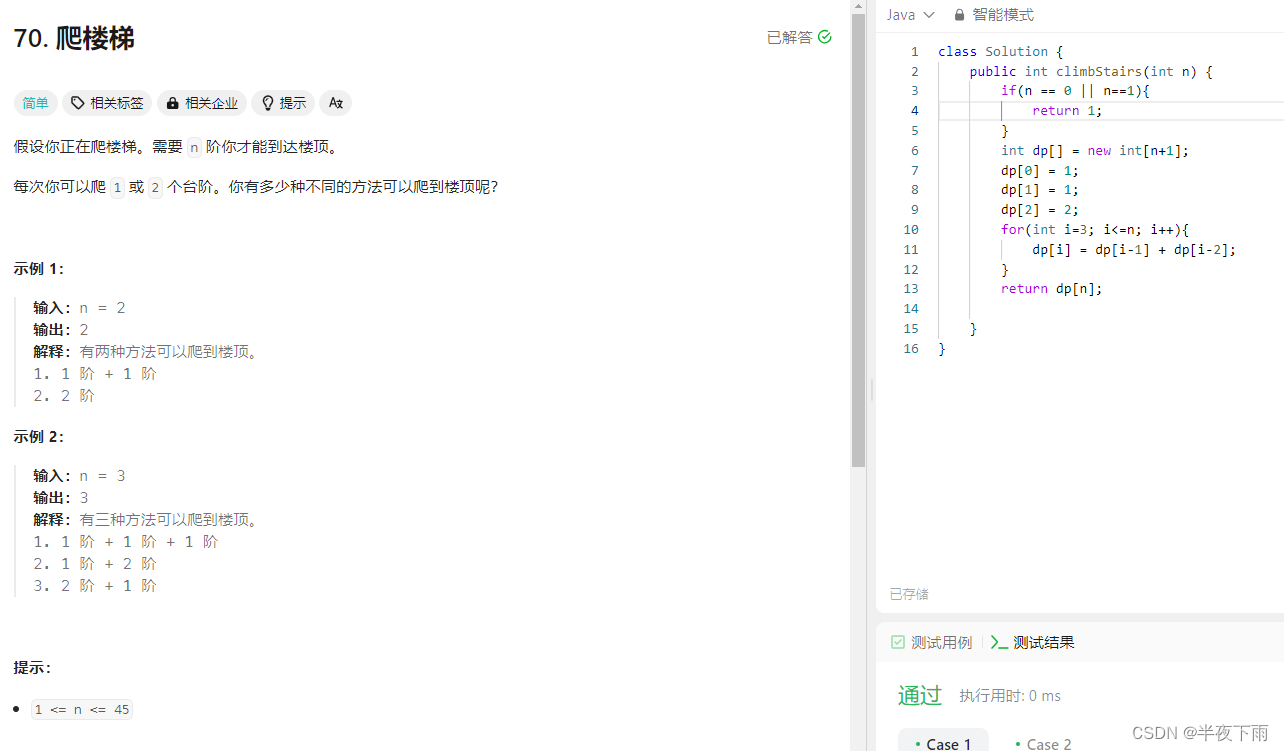
第一题：爬楼梯（还有拓展一次爬多阶，做法相同）

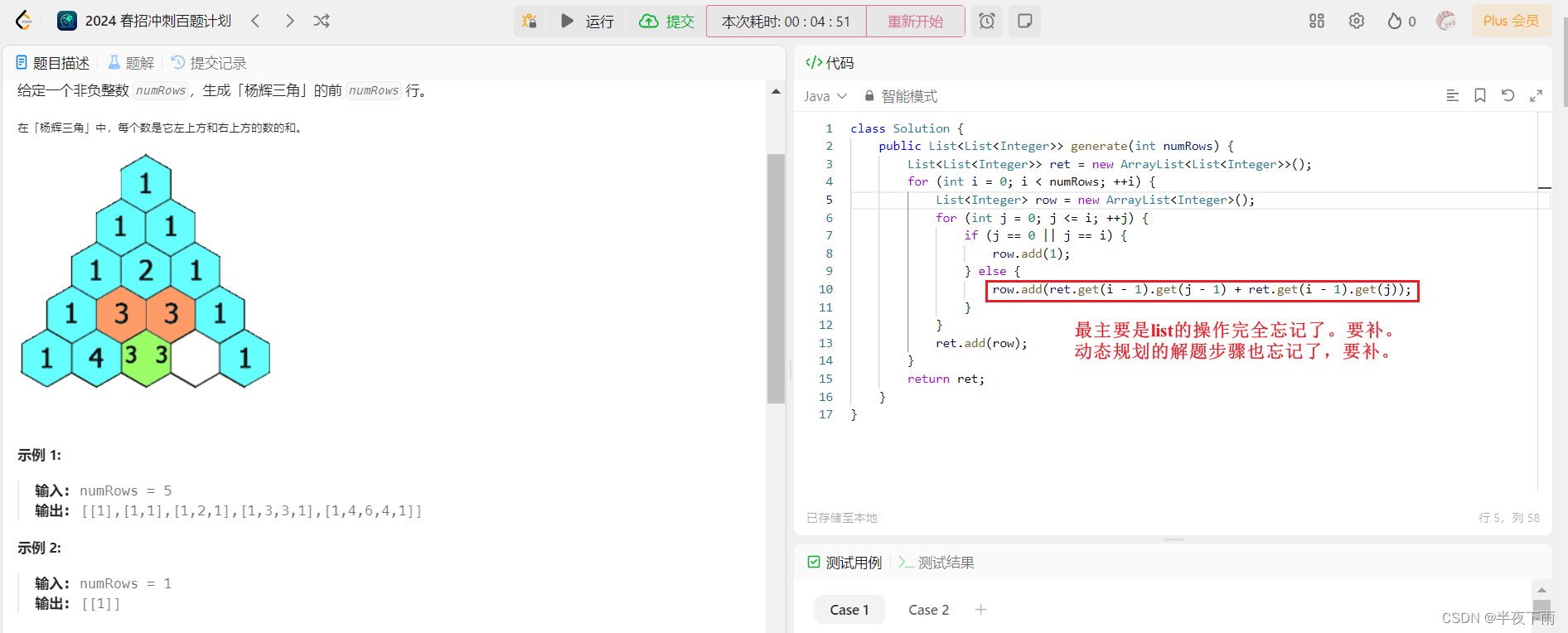
第二题：杨辉三角

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> ret = new ArrayList<List<Integer>>();
        for (int i = 0; i < numRows; ++i) {
            List<Integer> row = new ArrayList<Integer>();
            for (int j = 0; j <= i; ++j) {
                if (j == 0 || j == i) {
                    row.add(1);
                } else {
                    row.add(ret.get(i - 1).get(j - 1) + ret.get(i - 1).get(j));
                }
            }
            ret.add(row);
        }
        return ret;
    }
}

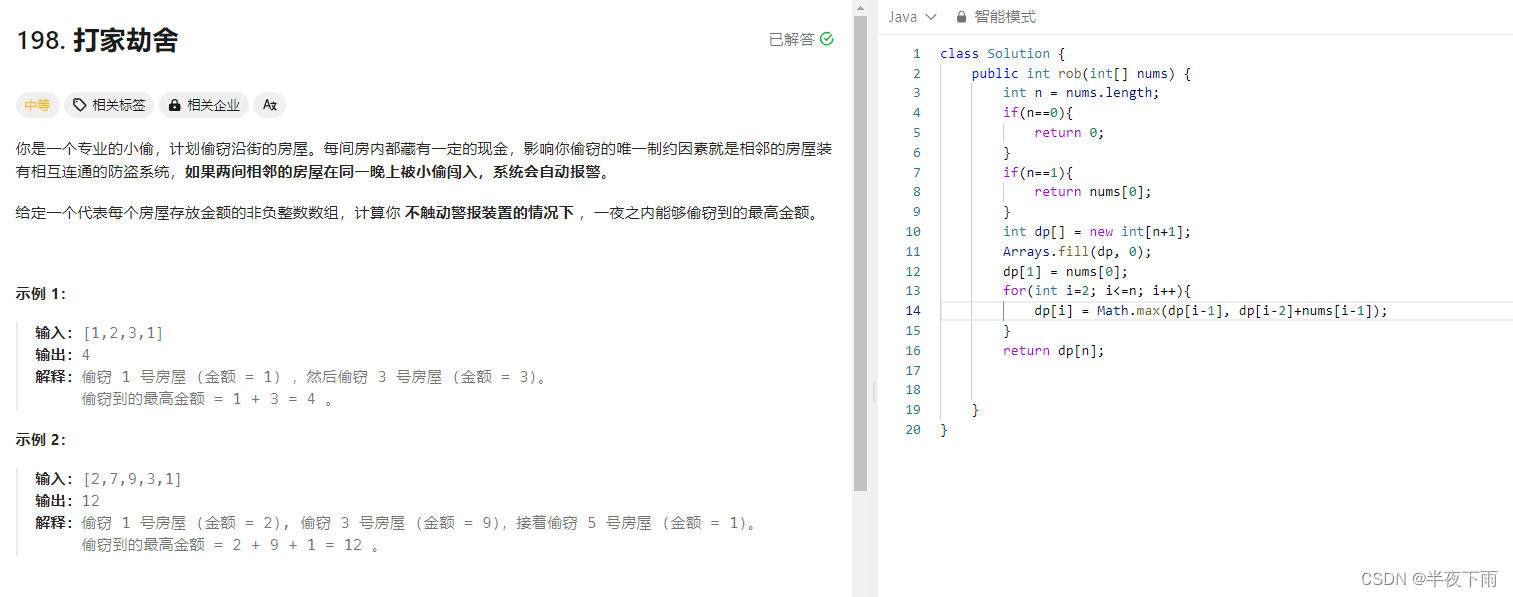
第三题：打家劫舍（非常基础的版本）

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        if(n==0){
            return 0;
        }
        if(n==1){
            return nums[0];
        }
        int dp[] = new int[n+1];
        Arrays.fill(dp, 0);
        dp[1] = nums[0];
        for(int i=2; i<=n; i++){
            dp[i] = Math.max(dp[i-1], dp[i-2]+nums[i-1]);
        }
        return dp[n];
        

    }
}

ps：这里的优化是空间上的优化，注意更新公式只涉及三个变量，因此可以用int temp = Math.max(curr, prev + i);替代数组，实现空间从O(n)到O(1)的转变。

（不熟悉的题型，重点复习）第四题：矩阵中的最长递增路径（深度搜索问题）

我面临的问题，从什么点出发，怎么保存搜索中的最大值。
每个点都走一遍。直到不能走再返回上一步。
我觉得我的代码出问题在于第二个问题。
学习了B站子烁爱学习这位up主的视频。

class Solution {
    int ma = 0;
    public int DFS(int[][] matrix, int x, int y, int value){
        // 递归结束条件
        if(x<0||x>=matrix.length||y<0||y>=matrix[0].length){
            return 0; //越界
        }
        if(matrix[x][y]<=value){
            return 0;
        }
        if(memo[x][y]!=0){
            return memo[x][y];
        }
        memo[x][y] = 1;
        int up = DFS(matrix, x, y-1, matrix[x][y]);
        int down = DFS(matrix, x, y+1, matrix[x][y]);
        int left = DFS(matrix, x-1, y, matrix[x][y]);
        int right = DFS(matrix, x+1, y, matrix[x][y]);
        memo[x][y] = Math.max(memo[x][y], Math.max(Math.max(up,down),Math.max(left,right))+1);
        return memo[x][y];
    }
    private int[][] memo;
    public int longestIncreasingPath(int[][] matrix) {
        int rows = matrix.length;
        if(rows < 1){
            return 0;
        }
        int cols = matrix[0].length;
        int result = Integer.MIN_VALUE;
        memo = new int[rows][cols];
        for(int[] m:memo){
            Arrays.fill(m, 0);
        }
        for(int i=0; i<rows; i++){
            for(int j=0; j<cols; j++){
                result = Math.max(result, DFS(matrix, i, j, Integer.MIN_VALUE));
            }
        }
        return result;
    }
}

第五题：青蛙过河：对Map不熟悉的惨烈下场。

首先还是想到要DFS，深度搜索嘛。
还是应用不上记忆化搜索这个方法，所以超时了。

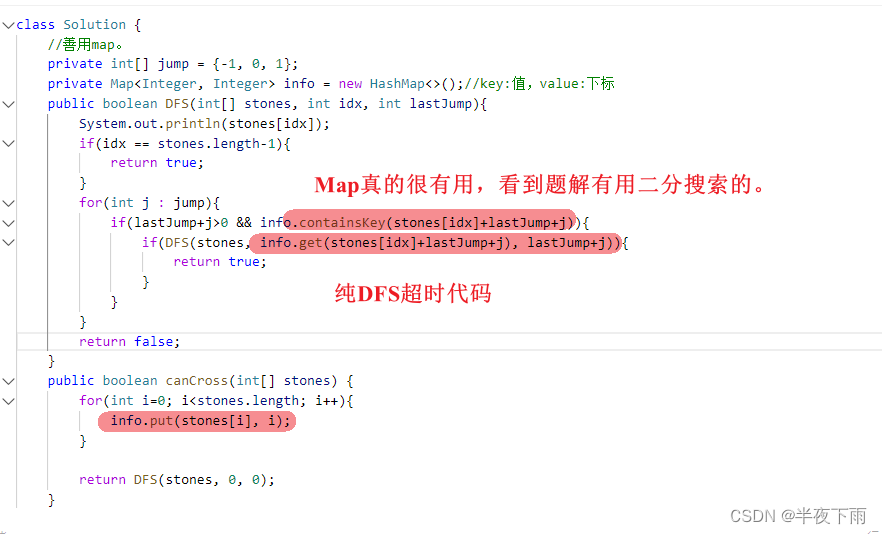
在看题解之前，先自己思考一下，能有什么地方需要记下来不重复搜索的，我觉得就是idx和jump的组合，如果已经搜索过，就不用搜索了。
出现的问题，如何确定第二维的维度？随便测试了1000，可以通过。

class Solution {
    //善用map。记忆化搜索int[][] recorded。
    private int[][] recorded;
    private int[] jump = {-1, 0, 1};
    private Map<Integer, Integer> info = new HashMap<>();//key:值，value:下标
    public boolean DFS(int[] stones, int idx, int lastJump){
        System.out.println(stones[idx]);
        if(idx == stones.length-1){
            return true;
        }
        for(int j : jump){
            if(lastJump+j>0 && info.containsKey(stones[idx]+lastJump+j)){
                if(recorded[info.get(stones[idx]+lastJump+j)][lastJump+j]==1){
                    continue;
                }
                if(DFS(stones, info.get(stones[idx]+lastJump+j), lastJump+j)){
                    return true;
                }
                recorded[info.get(stones[idx]+lastJump+j)][lastJump+j] = 1;

            }
        }
        return false;         
    }
    public boolean canCross(int[] stones) {
        if(stones.length<=1){
            return true;
        }
        recorded = new int[stones.length][1000];
        for(int i=0; i<stones.length; i++){
            info.put(stones[i], i);   
            Arrays.fill(recorded[i], 0);
        }
        return DFS(stones, 0, 0);
    }
    
}

但是目前为止还是没有用到动态规划。我隐约记得，动态规划就是把递归的过程转化为 更新公式。
动态规划：dp数组维度与含义，遍历方向，更新公式。
好难，看得是官方的题解。更新公式和之前在代码随想录里做过的一题好像。怎么说呢，就是难呀，在动态规划里面。还涉及了比较难想的优化问题。

class Solution {
    public boolean canCross(int[] stones) {
        int n = stones.length;
        boolean[][] dp = new boolean[n][n];
        dp[0][0] = true;
        for (int i = 1; i < n; ++i) {
            if (stones[i] - stones[i - 1] > i) {
                return false;
            }
        }
        for (int i = 1; i < n; ++i) {
            for (int j = i - 1; j >= 0; --j) {
                int k = stones[i] - stones[j];
                if (k > j + 1) {
                    break;
                }
                dp[i][k] = dp[j][k - 1] || dp[j][k] || dp[j][k + 1];
                if (i == n - 1 && dp[i][k]) {
                    return true;
                }
            }
        }
        return false;
    }
}

作者：力扣官方题解
链接：https://leetcode.cn/problems/frog-jump/solutions/746996/qing-wa-guo-he-by-leetcode-solution-mbuo/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

第六题：分割等和子集

做过无数次的，还是被难住。找不到动态思路（可恶）。有了背包作为基础，背包知识又全忘记了。（痛苦）

class Solution {
    public boolean canPartition(int[] nums) {
        //背包的思想（有想到过，但是不坚定，所以去看了以前的笔记。）
        //就是努力将背包装满，直到极限，看背包是否刚好装满。0-1背包问题。
        int average = 0;
        for(int n: nums){
            average += n;
        }
        if(average%2!=0){
            return false;
        }
        average = average/2;
        int dp[] = new int[average+1];
        Arrays.fill(dp, 0);
        for(int i=0; i<nums.length; i++){
            for(int j=average; j>=nums[i]; j--){
                dp[j] = Math.max(dp[j], dp[j-nums[i]]+nums[i]);
            }
        }
        return dp[average]==average;
    }
}

第七题：最长递增子序列

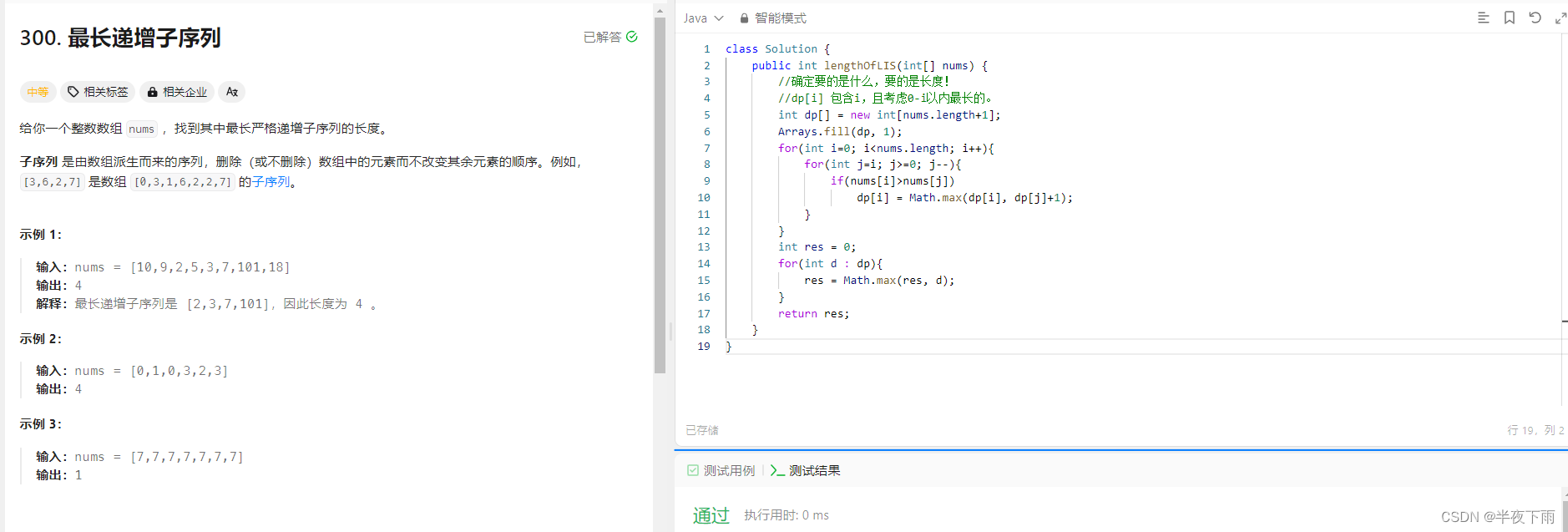
有了上一题的经验，基本能够独立完成这一题了。当然，也是因为这一题比较简单。

class Solution {
    public int lengthOfLIS(int[] nums) {
        //确定要的是什么，要的是长度！
        //dp[i] 包含i，且考虑0-i以内最长的。
        int dp[] = new int[nums.length+1];
        Arrays.fill(dp, 1);
        for(int i=0; i<nums.length; i++){
            for(int j=i; j>=0; j--){
                if(nums[i]>nums[j])
                    dp[i] = Math.max(dp[i], dp[j]+1);
            }
        }
        int res = 0;
        for(int d : dp){
            res = Math.max(res, d);
        }
        return res;
    }
}

第八题：最大矩形（好讨人厌的题目）真的不会

折磨了我好几天，网络上关于这题的讲解也很少。折磨了自己好几天，一直不愿意动手。
先确定一下解题步骤，然后再上手写吧。
完全依据leetcode官方解法的暴力解法做出来的。

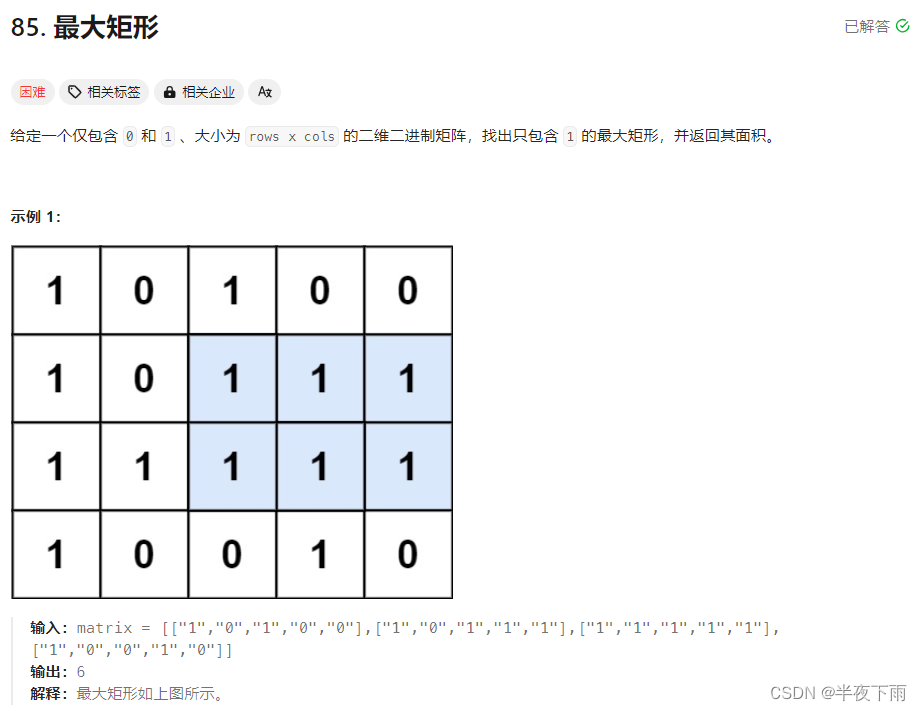
class Solution {
    public int maximalRectangle(char[][] matrix) {
        //1很不想写，觉得这题好傻逼，不对，是我好傻逼，一定写不出来。算了算了，傻逼也会抄答案的，一比一抄，应该是没有问题的。
        //leetcode题解，第一句话就是，枚举，一个作为左上角坐标，一个作为右下角坐标，判断该矩形符不符合要求，但是复杂度过高，完全没有。
        //暴力解法1
        //1.1 计算每一个元素左边连续1的个数，用left[i][j]记录
        int rows = matrix.length;
        int cols = matrix[0].length;
        int left[][] = new int[rows][cols];
        for(int row=0; row<rows; row++){
            Arrays.fill(left[row], 0);
            for(int col=0; col<cols; col++){
                if(col == 0&&matrix[row][col]=='1'){
                    left[row][col] = 1;
                }else{
                    if(matrix[row][col]=='1'){
                        left[row][col] = left[row][col-1] + 1;
                    }
                }
                System.out.print(left[row][col] + " ");
            }
            System.out.print("\n");     
        }
        //1.2 枚举每一个元素作为右下角的全1矩阵。重点，对于每一个matrix[i][j] 只要考虑left[0-i][j]就能得到所有可能。
        //对于1.2的另一种看法，可以转化为84题，柱状图中最大矩形面积。
        int maxArea = 0;
        int width = Integer.MAX_VALUE;
        int height = 0;
        for(int row=0; row<rows; row++){
            for(int col=0; col<cols; col++){
                if(matrix[row][col]=='1'){
                    width = Integer.MAX_VALUE;
                    for(int k=row; k>=0; k--){
                        width = Math.min(width, left[k][col]);
                        height = row - k + 1;
                        maxArea = Math.max(maxArea, width*height);
                    }
                }
                System.out.print(maxArea + " ");
                
            } 
            System.out.print("\n"); 
        }
        return maxArea;

    }
}

与题解相比自己的问题

这种方法，时间复杂度（计算left：mn，遍历计算mn*m，总的：mmn）。空间复杂度mn，存放left。
要优化的部分肯定是遍历计算，这也是84题的单调栈！

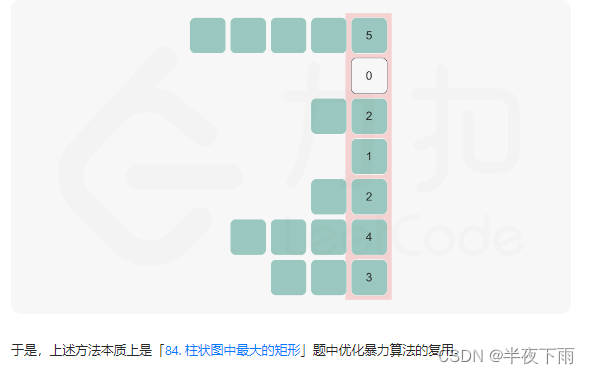
leetcode的单调栈优化，和代码随想录的思路还是不一样的。

//2.2 单调栈优化：存什么，栈内元素是递增还是递减，每个元素与栈顶的关系处理（><=）。
        //存下标（知道下标就一定知道value）
        //重点还是怎么判断，我要的是递增栈还是递减栈（看答案知道是递增栈）
        int maxArea = 0;
        //对每一列都执行一次单调栈
        for(int col=0; col<cols; col++){
            int[] up = new int[rows];
            int[] down = new int[rows];
            Deque<Integer> stack = new LinkedList<Integer>();
            for(int row=0; row<rows; row++){
                while(!stack.isEmpty()&&left[stack.peek()][col] >= left[row][col]){
                    stack.pop();
                }
                up[row] = stack.isEmpty() ? -1:stack.peek();
                stack.push(row);
                System.out.print(up[row]+ " ");  
            } 
            System.out.print("\n"); 
            stack.clear();
            for (int row = rows - 1; row >= 0; row--) {
                while (!stack.isEmpty() && left[stack.peek()][col] >= left[row][col]) {
                    stack.pop();
                }
                down[row] = stack.isEmpty() ? rows : stack.peek();
                stack.push(row);
                System.out.print(down[row]+ " ");  
            } 
            System.out.print("\n"); 

            for (int row = 0; row < rows; row++) {
                int height = down[row] - up[row] - 1;
                int area = height * left[row][col];
                maxArea = Math.max(maxArea, area);
            }
        }

第九题：戳气球

在这里插入图片描述

class Solution {
    int val[];
    
    public int maxCoins(int[] nums) {
        val = new int[nums.length+2];
        for(int i=1; i<=nums.length; i++){
            val[i] = nums[i-1];
        }
        val[0] = val[nums.length+1] = 1;
        //动态规划思路：记忆化搜索是自顶向下，转化一下，变成自底向上的动态规划，利用空间换取时间。
        //2.动态规划的问题：dp几维，含义是什么，如何初始化，怎么更新。
        //2.1dp二维，表示和记忆化搜索的solve函数一样。
        int dp[][] = new int[nums.length+2][nums.length+2];
        //2.2初始化
        for(int i=0; i<nums.length+1; i++){
            Arrays.fill(dp[i], 0);
        }

        //2.3如何更新
        for(int i=nums.length-1; i>=0; i--){
            for(int j=i+2; j<=nums.length+1; j++){
                for(int k=i+1; k<j; k++){//解空间
                    int tmp = val[i]*val[k]*val[j];
                    tmp = tmp + dp[i][k] + dp[k][j];//子问题
                    dp[i][j] = Math.max(tmp, dp[i][j]);
                }
            }
        }
        return dp[0][nums.length+1];
    }
}
// class Solution {
//     int val[];
//     int reds[][];
//     public int maxCoins(int[] nums) {
//         //首先就想到了最暴力的方法，回溯。枚举每一种可能，但显然会超时很多。4！
//         //根据官方题解写
//         //1.记忆化搜索，加气球，避免重复计算，存储solve
//         //1.1创建val，在nums前后添加值为1的元素，防止越界
//         val = new int[nums.length+2];
//         for(int i=1; i<=nums.length; i++){
//             val[i] = nums[i-1];
//         }
//         val[0] = val[nums.length+1] = 1;
//         //1.2遍历，并记忆搜索过程solve[i][j] = max(val[i]*val[k]*val[j])(k∈（i+1，j-1）)。搜索过程
//         reds = new int[nums.length+2][nums.length+2];
//         for(int i=0; i<nums.length; i++){
//             Arrays.fill(reds[i], -1);
//         }
//         return solve(0, nums.length+1);


//     }
//     private int solve(int i, int j){
//         if(i>=j-1){//结束条件
//             return 0;
//         }
//         if(reds[i][j]!=-1){
//             return reds[i][j];
//         }
//         int tmp=0;
//         for(int k=i+1; k<j; k++){//解空间
//             tmp = val[i]*val[k]*val[j];
//             tmp = tmp + solve(i, k) + solve(k, j);//子问题
//             reds[i][j] = Math.max(tmp, reds[i][j]);
//         }
//         return reds[i][j];

//     }
// }