《深入理解计算机系统》 练习题2.48 2.49 IEEE浮点表示

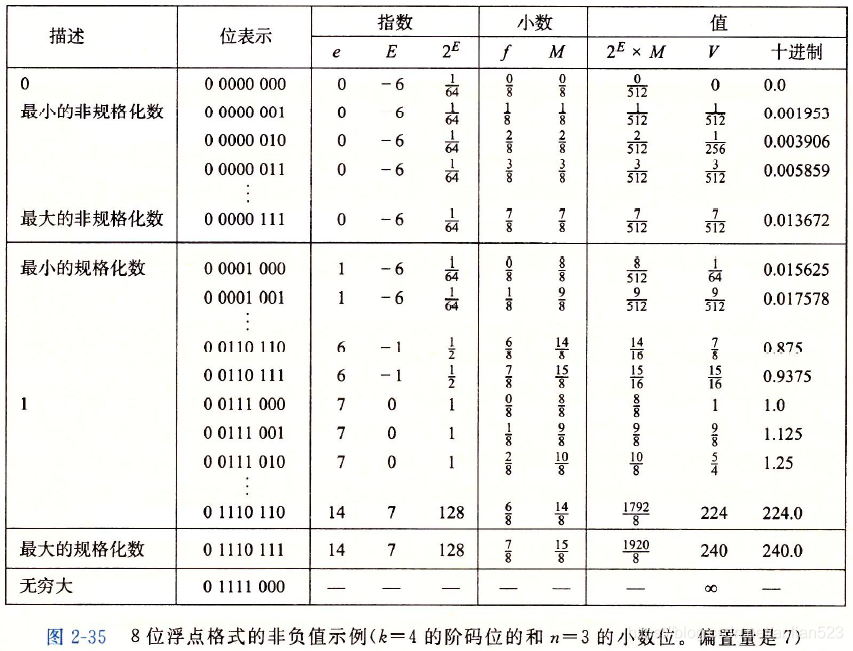
IEEE浮点表示

关于IEEE浮点表示的具体讲解，本文就不班门弄斧了，请自行阅读书籍。本文将进行必要总结再加上自己的理解。
IEEE浮点标准用$V=(-1{)}^s\times M\times 2^E$的形式来表示一个数：

1）符号（sign）：s决定这个数是正数还是负数，注意会有正0和负0的区分。

2）尾数（significand）：M是一个二进制小数，设$\epsilon$为$\frac{1}{2^n}$，它的范围可以是1~2-$\epsilon$（此时是规则化数的小数部分），也可以是0~1-$\epsilon$（此时是非规则化数的小数部分）。
尾数有n位二进制，代表着n位无符号数的范围[0, $2^n$-1]。假如这个无符号数的取值为frac，那么$f=\frac{frac}{2^n}$。M可能为$f$，当此时为非规格化数时。M也可能为$1+f$，当此时为规格化数时。给出$f$的范围$$\frac{0}{2^n}\sim \frac{2^n-1}{2^n}$$
对于加1的解释则为：在规格化数中，整数部分的1是当它一直存在的。

3）阶码（exponent）：E对上面的尾数进行加权，这个权重是2的E次幂（可能是负的）即$2^E$。权重的范围为
$$2^{2-2^{k-1}}\sim 2^{2^{k-1}-1}$$
阶码有k位二进制，代表着k位无符号数的范围[0, $2^k$-1]，但实际只能取[0, $2^k$-2]。假如这个无符号数的取值为$e$。
偏置bias为$2^{k-1}-1$。
有$E=e-bias$，现在开始证明上述范围：当$e$取最小值0或1时，则$E=1-(2^{k-1}-1)=2-2^{k-1}$。证明了范围的左边；
当$e$取最大值$2^k$-2时，则$E=2^k-2-(2^{k-1}-1)=2^{k-1}-1$。证明了范围的右边；

在规格化数中，阶码的范围是[1, $2^k$-2]，因为规格化数的阶码的二进制位不能全为0，也不能全为1。且一个浮点数，是否规格也是看它的阶码。

当阶码全为0，此时为非规格化数。则$e$为0，但不能执行$E=0-bias$，还是得执行$E=1-bias$。这是为了最大的非规格化数和最小的规格化数之间的平滑过渡（这里指二进制排序）。所以当$e$取最小值0或1时，它们的$E$都是一样的，但前者是非规格化数，对应的小数是$f$；后者是规格化数，对应的小数是$1+f$。
所有的规格化数，对应的小数都是$1+f$。

当阶码全为1，此时为非规格化数。如果尾数的二进制全为0时，则代表正无穷；如果是其他情况，则代表$NaN$ Not a Number。这也解释了为什么阶码最大取的是$2^k$-2，因为$2^k$-1时要么是无穷，要么是$NaN$。

单精度float中，一共32位，k为8，n为23.
双精度double中，一共64位，k为11，n为52.

2.48

整数3510593的十六进制表示为0x00359141
单精度浮点数3510593.0的十六进制表示为0x4a564504, 则这两个数的关系。

float中，k为8，n为23。
偏移量Bias=$2^{8-1}$-1=128-1=127.

数值	二进制
3510593	0000 0000 0011 0101 1001 0001 0100 0001
3510593.0	0100 1010 0101 0110 0100 0101 0000 0100

3510593 = 0000 0000 001.1 0101 1001 0001 0100 0001 * $2^{21}$。小数点往前移动了21次，总共的有效位是22位，由于整数部分的1总是可以被隐式地表示，所以只需要往前移动21位。

去除最高位的1, 小数部分最后加2个0达到23个，则小数部分为1 0101 1001 0001 0100 0001 00。

阶码部分$E=e-bias$即$21=e-127$，则$e=148$，其无符号的二进制表示为1001 0100，刚好k为8，刚好够表示的。

符号位为0，即为正。

则从整数转成单精度则为：
[0] [1001 0100] [1 0101 1001 0001 0100 0001 00]
= 0100 1010 0101 0110 0100 0101 0000 0100

数值	…	重复部分	…
3510593	0000 0000 001	1 0101 1001 0001 0100 0001
3510593.0	0100 1010 0	101 0110 0100 0101 0000 01	00

从上表可以明显看出重复部分。

2.49

在浮点数能否有效的正整数范围，与尾数部分即n的大小有关（从整数往浮点数转换可以发现，除开被暂时忽略的整部部分的1，能否转成浮点数，关键看n是否大于等于小数部分的有效位个数，通俗的讲就是这n位能否装下所有的小数部分），即能表示n+1位的二进制无符号整数。
n+1位的二进制无符号整数的最大是$2^{n+1}-1$。那么刚好不能表示的整数则为$2^{n+1}-1+1=2^{n+1}$。
注意上述答案是错误的。
实际上$2^{n+1}$是可以表示的，因为$2^{n+1}$的无符号二进制肯定是1 后接n+1个0（$2^{n+1}$是第n+2位的权值，从第1位开始），而此题说了阶码范围肯定够大，那么小数是0可以表示，而阶码部分也可以保证了，所以实际上是可以表示的。
而$2^{n+1}+1$则不可以表示，因为$2^{n+1}+1$的无符号二进制肯定是1 后接n个0 再接个1，除开前面属于整数部分的1，后面的小数还有n+1位呢（这里可不是全是0了啊），只有n位的浮点肯定不够表示呀。
答案为$2^{n+1}+1$。

参考链接：
[1] https://github.com/haiiiiiyun/book_exercises/blob/master/csapp-v3/chap2/2.43-2.54.txt