什么是图?
在计算机中,图结构也是一种非常常见的数据结构。图论也是一个非常大的话题
图结构是一种与树结构有些相似的数据结构。
图论是数学的一个分支,并且,在数学的概念上,树是图的一种。
图主要研究的目的是事物之间的关系,顶点代表事物,边代表两个事物间的关系。
图在生活中的应用场景:
人与人之间的关系(比如六度空间理论),地点之间的联系图(地图App,就是通过图来计算最短路径或最优路径)
图的特点
- 一组顶点:通常用V(vertex)表示顶点的集合
- 一组边:通常用E(edge)表示边的集合
边就是顶点之间的连线
边可以是有向的也可以是无向的
比如A -> B:表示有向; A–B:表示无向
图的常见术语
- 顶点:表示图中的一个节点。比如地图中某个位置的站点
- 边: 两个顶点之间的连线。
- 相邻顶点:由一条边连接在一起的顶点称为相邻顶点。
- 度:与该顶点相关联的边的个数。比如一个两个顶点的回路,顶点就有两个度
- 路径:顶点V1,V2…Vn的一个连续序列。
- 简单路径:不包含重复的顶点的路径
- 回路:第一个顶点和最后一个顶点相同的路径称为回路
- 无向图:顶点之间的边是没有方向的
- 有向图:顶点之间的边是有向的。
- 无权图:边没有携带权重,无权图的边称为是没有意义的。
- 带权图:带权图中的边带有一定的权重。权重可以是任意希望表示的数据:比如距离,耗费的事件,价格等。
图的表示
怎么在程序中表示图?
一个图包含很多顶点,另外包含顶点和顶点之间的连线(边)这两个都是非常重要的图信息,因此都需要在程序中体现出来
顶点的表示,可以抽象成ABCD,或者一些别的字符。然, A, B,C,D有可能还表示其他含义的数据(比如村庄的名字)
那么边怎么表示呢?
因为边是两个顶点之间的关系,所以表示起来会稍微麻烦一些.下面,我们具体讨论一下常见的表示方式
常见的表示图的方式:
邻接矩阵
- 邻接矩阵让每个节点和一个整数关联,该整数作为数组的下标值
- 用一个二维数组来表示顶点之间的连接

如图:二维数组中,用0表示没有连线,1表示有连线。通过二维数组,我们可以很快的找到一个顶点和哪些顶点有连线(比如A顶点,只需要遍历第一行即可)。另外,A - A,B - B(也就是顶点到自己的连线),通常使用O表示.
邻接矩阵的问题:
邻接矩阵有一个比较严重的问题,就是如果图是一个稀疏图,那么矩阵中将存在大量的0,这意味着我们浪费了计算机存储空间来表示根本不存在的边。
邻接表
另外一种常用的表示图的方式:邻接表
邻接表由图中每个顶点以及和顶点相邻的顶点列表组成。这个列表有很多中方式来存储:数组/链表/字典(哈希表)都可以
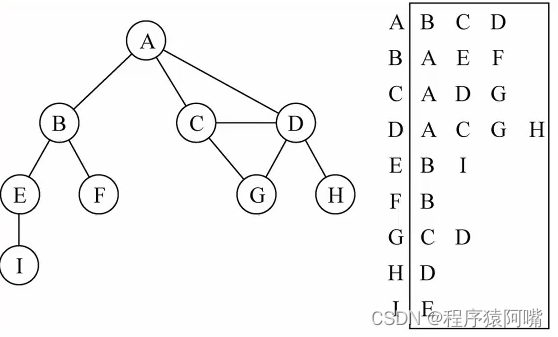
图片比较容易理解:比如我们要表示和A顶点有关联的顶点(边),A和B/C/D有边,
那么我们可以通过A找到对应的数组/链表/字典,再取出其中的内容就可以。
邻接表的问题:
邻接表计算"出度"是比较简单的(出度:指向别人的数量,入度:指向自己的数量),邻接表如果需要计算有向图的"入度",那么是一件非常麻烦的事情,它必须构造一个“逆邻接表”,才能有效的计算“入度”,但开发中“入度”相对用的比较少。
封装图结构
// 封装图结构(用邻接表的方式封装)
class Graph {
constructor() {
// 属性:顶点(数组)/边(字典)
this.vertexs = [] // 顶点
this.edges = new Map() // 边
}
// 添加顶点的方法
addVertex(v) {
// 首先添加顶点
this.vertexs.push(v)
// 添加顶点的时候,初始化一个数组,存储相邻的顶点
this.edges.set(v, [])
}
// 添加边的方法,传入两个顶点(无向图的添加)
addEdge(v1, v2) {
this.edges.get(v1).push(v2)
this.edges.get(v2).push(v1)
}
// 实现toString方法
toString() {
// 1.定义字符串,保存最终的结果
let res = ''
let val
// 2.遍历所有的顶点,以及顶点对应的边
this.vertexs.forEach(item => {
res += item + '->'
this.edges.get(item).forEach(item => {
res += item + ','
// console.log(key, value);
})
res += '\n'
})
return res
}
}
// 测试代码
// 1.实例化图结构
let graph = new Graph()
const myVerTexes = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']
// 2.添加顶点
myVerTexes.forEach(item => {
graph.addVertex(item)
})
// 3.添加边
graph.addEdge('A', 'B')
graph.addEdge('A', 'C')
graph.addEdge('A', 'D')
graph.addEdge('C', 'D')
graph.addEdge('C', 'G')
graph.addEdge('D', 'G')
graph.addEdge('D', 'H')
graph.addEdge('B', 'E')
graph.addEdge('B', 'F')
graph.addEdge('E', 'I')
alert(graph)
测试结果:

图的遍历
图的遍历思想:
- 图的遍历思想和树的遍历思想是一样的。
- 图的遍历意味着需要将图中每个顶点访问一遍,并且不能有重复的访问
有两种算法可以对图进行遍历
- 广度优先搜索(Breadth-First Search,简称BFS)。基于队列,入队的顶点先被探索
- 深度优先搜索(Depth-First Search,简称DFS) 。基于栈或使用递归,通过将顶点存入栈中,顶点是沿着路径被探索的,存在新的相邻点就去访问
- 两种遍历算法,都需要明确指定第一个被访问的顶点.
用三种颜色表示顶点的状态
- 白色:表示该顶点还没被访问
- 灰色:表示该顶点被访问过,但并未被探索过
- 黑色:表示该顶点被访问过且被完全探索过
广度优先搜索
广度优先搜索会从指定的第一个顶点开始遍历图,先访问其所有的相邻点,一次访问一层,也就是先宽度后深度的访问顶点
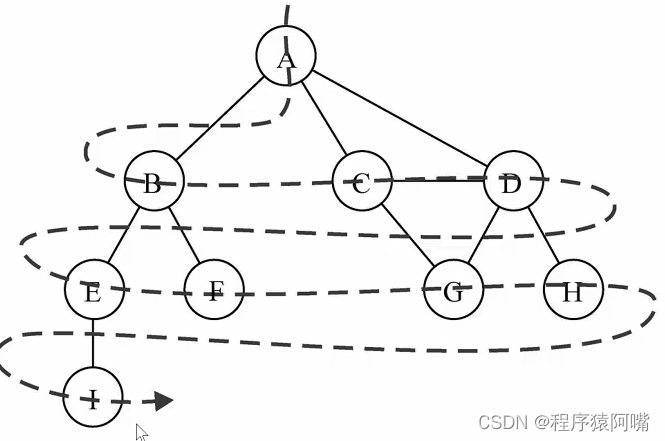
如图,访问顺序为:A-B-C-D-E-F-G-H-I
代码实现思路:
基于队列(先进先出)实现:
- 首先创建一个队列Q
- 将V点标注为灰色,V加入队列Q
- 如果Q非空,执行以下步骤
- 将V从Q中出队
- 将V标注为被发现的灰色
- 将V所有的未被访问过的邻接点标注为白色,加入到队列中
- 将V标注为黑色
代码实现:
// 初始化状态颜色
initializeColor() {
let colors = []
this.vertexs.forEach(item => {
// 初始化为白色
colors[item] = 'white'
})
return colors
}
// 广度优先搜索,传入两个参数:初始化的顶点和处理函数
bfs(initV, handler) {
// debugger
// 1.所有顶点初始化颜色
let colors = this.initializeColor()
// 2.创建队列
let queue = new Queue()
// 3.顶点入队
queue.enqueue(initV)
// 4.循环从队列中取出元素
while (!queue.isEmpty()) {
// 4.1 从队列中取出一个顶点
let v = queue.dequeue()
// 4.2 获取和顶点相邻的其他顶点
let vList = this.edges.get(v)
// 4.3 将v的颜色设置为灰色
colors[v] = 'gray'
// 4.4 遍历所有相邻的其他顶点,并且加入到队列中
vList.forEach((item) => {
// 此步判断是否访问过,只入队没访问过的,避免重复入队
if (colors[item] == 'white') {
// 访问过后改变颜色
colors[item] = 'gray'
// 入队
queue.enqueue(item)
}
})
// 4.5 处理节点
handler(v)
// 4.6 访问完的点为黑色
colors[v] = 'black'
}
}
测试代码:
// 测试bfs 这里传入第一个节点
let res = ''
graph.bfs(graph.vertexs[0], function (v) {
res += v + ' '
})
alert(res)

图的广度优先搜索类似于树的层序遍历
深度优先搜索
深度优先搜索的思路:
- 深度优先搜索算法会从第一个指定的顶点开始遍历图,沿着路径直到这条路径最后被访问完(一条道走到黑)
- 接着原路回退并探索下一条路径
- 类似树的先序遍历
深度优先搜索算法的实现思路:
- 广度优先搜索算法我们使用的是队列,这里可以使用栈完成,也可以使用递归,为了方便代码书写,这里使用递归(递归本质上就是函数栈的调用)。

如图:访问顺序为:
- 先访问A节点,在访问A节点的相邻节点,按照存储顺序是B
- 访问B的相邻节点E,访问E的相邻节点I
- I没有未访问过的节点,回溯到B,访问F
- F回溯到A,访问C
- 访问C相邻节点D
- 访问D相邻节点G
- 回溯到D,访问D相邻节点H
- 回溯到A节点访问结束
代码实现:
// 深度优先搜索
dfs(initV, handler) {
// 1.所有顶点初始化颜色
let colors = this.initializeColor()
// 2.从某个顶点开始依次递归访问
this.dfsVisit(initV, colors, handler)
}
// dfs的递归函数
dfsVisit(v, colors, handler) {
// 1.将颜色设置为灰色
colors[v] = 'gray'
// 2.处理v顶点
handler(v)
// 3.访问v相连的顶点
let vList = this.edges.get(v)
vList.forEach(item => {
if (colors[item] == 'white') {
this.dfsVisit(item, colors, handler)
}
})
// 4.将v设置为黑色
colors[v] = 'black'
}
测试代码:
// 测试dfs
res = ''
graph.dfs(graph.vertexs[0], function (v) {
res += v + ' '
})
alert(res)
测试结果:












 本文深入探讨了图的定义、特点及其在现实生活中的应用,如人际关系和地图导航。介绍了图的主要术语,如顶点、边、度、路径等,并详细阐述了无向图与有向图的区别。接着,文章讨论了图的两种常见表示方法:邻接矩阵和邻接表,以及它们的优缺点。最后,讲解了图的遍历算法,包括广度优先搜索(BFS)和深度优先搜索(DFS),并给出了相应的代码实现。
本文深入探讨了图的定义、特点及其在现实生活中的应用,如人际关系和地图导航。介绍了图的主要术语,如顶点、边、度、路径等,并详细阐述了无向图与有向图的区别。接着,文章讨论了图的两种常见表示方法:邻接矩阵和邻接表,以及它们的优缺点。最后,讲解了图的遍历算法,包括广度优先搜索(BFS)和深度优先搜索(DFS),并给出了相应的代码实现。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








