经验风险最小化、交叉验证、特征选择(提取)
1、经验风险最小化
经验风险最小化(Empirical Risk Minimization)是机器学习的一个原则,它可以给出学习算法的性能边界。
机器学习的目的,就是根据一些训练样本寻找最优函数,使得函数对输入的预测与真实值之间的期望风险(类似于“误差”的概念)最小。
期望风险依赖于输入和输出的映射关系,而这个映射却是未知的;我们所掌握的,只有有限的训练样本及其输出。因此很自然的想到,用有限样本的期望值来代替理想的期望值。
训练样本已知,因此称作“经验数据”;由它计算出的误差,被称为“经验风险”;通过使经验风险最小来逼近期望风险最小的目标,就是“经验风险最小化”原则。
输入空间记作X、输出空间记作Y、两者的联合概率分布记作P(X,Y)、学习到的模型记作 。
。
定义损失函数L(h(x),y)用来衡量预测值h(x)和真实值y的差异。那么模型h(x)的风险被定义为:
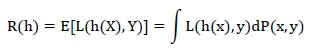
也就是损失函数的期望,称为“期望风险”。
多数场景下,联合概率密度是未知的。此时,我们可以考察训练集上的风险(损失),用它的期望值来代替真实值;训练集上的风险就是“经验风险”:
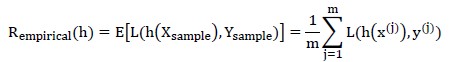
选择经验风险最小的模型,表述为:
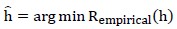
2、交叉验证&模型选择的问题提出
面临一个机器学习问题(例如拟合一组样本点)时,通常有多种模型可选(线性拟合、多项式拟合);一般来说,我们期望最终模型在偏差和方差之间达到平衡。
若简单的在全部样本上做拟合,那么多项式拟合的偏差必定低于线性拟合(例如线性不可分样本集,却可能用曲线做分隔);但是很容易出现“过拟合”现象。这就违背了我们的要求:在偏差(bias)和方差(variance)之间折中。
交叉验证就是用来解决这个问题。
在选择好模型之后(例如敲定了用线性拟合方法)就可以做拟合,但是我们可能需要从样本输入信息中提炼出重要信息。
具体来说,样本输入可能含有n个维度,那么:①n可能太多使得样本数量相对少,拟合效果不佳;②各个维度对结果的影响是不同的(例如“所在城市”可能是“房价”的首要因素、“附近公共交通”相对影响就很小),最好能剔除无用维度,留着反而是干扰;③某些维度或许可以糅合成一个维度,再做拟合,这样就达到了降维的效果。
特征选择&特征提取就是用于样本输入的维度太高的场景下。两者都可以降维,不同点在于:前者是简单的筛选已有的特征、后者可能会糅合一些已有特征作为新的特征。
3、交叉验证
全部样本记作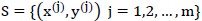 ;候选模型记作
;候选模型记作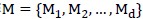 。
。
以“经验风险最小化”原则筛选最优模型。
最直观的筛选方法,就是对每个模型,用全部样本做拟合并计算拟合的偏差;而后选出偏差最小的那个模型作为最终结果。
其不足之处也很明显:只顾着偏差(bias)最小,却可能使方差(variance)非常大,即出现过拟合现象。
“简单交叉验证”
为了解决过拟合问题,最直接的办法就是:将样本集分为训练集&测试集;用前者学习出模型,再用后者计算该模型的误差。
其原理是,训练集&测试集可以看做没有内在关联的,因此有理由认为,这时的经验误差接近于“泛化误差”(generalization error)。这样便隐含的避免了过拟合问题。
过拟合问题貌似很严重的样子。但实际上,在按前述方法确定选用哪种模型后,为了确定该种模型在当前问题里的具体参数,一般可以在全体样本集上做训练;显然数据量越多越好,这时过拟合似乎又不那么重要了。在选择不同种类的模型时强调bias和variance的平衡,大概是为了公平对待各种模型(不然线性拟合在多项式拟合面前总是完败)。
这个方法仍然有不足:①确定最优模型的种类,只是在部分样本上选出来的;②若样本不多,那分为两个子集后,数据就更稀疏了。
“k-折叠交叉验证”(k – fold cross validation)
步骤如下:
(1)样本集合划分为k个不相交的子集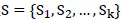 ;
;
(2)遍历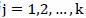 ;以
;以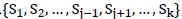 为训练集、
为训练集、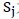 为测试集,对于当前候选模型做训练,并在
为测试集,对于当前候选模型做训练,并在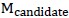 上计算经验误差;
上计算经验误差;
(3)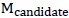 的经验误差就是步骤(2)中k个误差的平均值。
的经验误差就是步骤(2)中k个误差的平均值。
最后再比较各候选模型的经验误差,选出最小的那个。很显然,k-折叠交叉验证避免了简单交叉验证的两个不足。
4、特征选择
样本输入信息可能有冗余,共n个维度不一定都与输出很相关;并且无用维度可能起干扰作用。特征选择就是从中选出重要维度,以提高学习效果。
样本j的输入为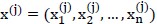 ;在选定特征组合
;在选定特征组合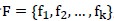 后,我们只对这些维度的输入数据学习,即
后,我们只对这些维度的输入数据学习,即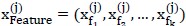 。
。
为判断这个组合的优劣,以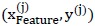 为样本集学习,看模型的经验误差;若经验误差小,则说明该特征组合较合理。
为样本集学习,看模型的经验误差;若经验误差小,则说明该特征组合较合理。
接下来讨论特征选择时的启发式方法。因为n个维度就有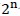 个不同组合,显然不可能一一尝试。
个不同组合,显然不可能一一尝试。
第一种是前向搜索法。
初始化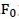 为空集;然后迭代
为空集;然后迭代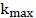 (特征个数的上限)次。第i次迭代的过程是,从不在
(特征个数的上限)次。第i次迭代的过程是,从不在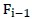 中的(n-i+1)个特征中找出这个特征
中的(n-i+1)个特征中找出这个特征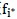 :以
:以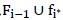 做学习,模型的误差最小;然后将
做学习,模型的误差最小;然后将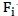 记作
记作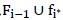 。
。
这样我们有了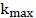 个不同的特征组合
个不同的特征组合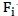 以及各自对应的模型。比较这些模型的误差,以最小误差模型对应的特征组合,为最终特征组合。
以及各自对应的模型。比较这些模型的误差,以最小误差模型对应的特征组合,为最终特征组合。
第二种是过滤特征选择(Filter feature selection)。
思路是对每个特征 衡量它相对于结果y的“信息量”,以此将n个特征降序排序;假设特征个数的阈值是
衡量它相对于结果y的“信息量”,以此将n个特征降序排序;假设特征个数的阈值是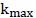 ,那么对
,那么对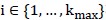 构建
构建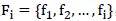 ,比较
,比较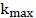 个
个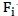 的模型误差并选择最小的那个。
的模型误差并选择最小的那个。
步骤一里的“信息量”可采用“互信息”来度量。注意若输入是连续值,则将其转化为离散值。
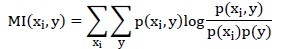
这个公式衡量的是 和y的独立性:若两者完全独立即
和y的独立性:若两者完全独立即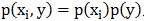 则MI=0;否则若两者非常相关,例如若
则MI=0;否则若两者非常相关,例如若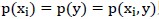 则MI为较大的正数。
则MI为较大的正数。
步骤二与前向搜索法的第二步类似,首先构建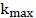 个模型,并从中选出误差最小的那个即可。
个模型,并从中选出误差最小的那个即可。
5、主成分分析(Principal Component Analysis)
样本输入往往有很多维度,其中某些维度确实与结果有关,但也可能存在噪声和冗余(冗余是指多个维度间可能强关联,例如km/h和miles/h)。PCA很给力的地方是真心可以减少冗余信息。
我们的目标是构造出k个新特征来替代初始的n个特征。
首要问题便是新特征的评价标准。信号处理的理论说,信号具有较大方差而噪声的方差较小;由此引申过来,我们希望在k个维度上,样本的方差尽可能大(感性理解,样本在某个维度上的投影,方差越大说明样本分散的越开,而不是拥挤在原点附近)。
先引入PCA中两个步骤:①样本输入如下处理:对每个维度减去该维度的均值(因此变换后样本均值为0)、再除以标准差(平衡不同维度值域差别);②构建出新的维度向量需要单位化。
如图,单位向量u代表一个维度,样本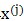 在u上的投影到原点的距离为
在u上的投影到原点的距离为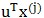 。
。
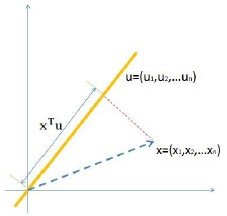
我们要求样本在维度u上的投影,其方差尽可能的大。注意PCA对样本的预处理,处理后的样本(也就是这里的输入)在各个初始维度上均值都是0,那么投影到u上均值依旧为0。因此,方差为:
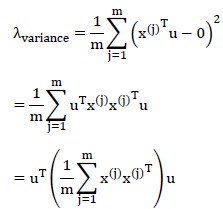
因为输入样本在每个维度上的均值为0,所以上式中括号内部分,就是输入的协方差矩阵,记作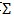 。注意到u是单位向量,因此有:
。注意到u是单位向量,因此有:
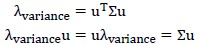
这是标准的矩阵求特征值、特征向量的形式。
所以,我们只需求对协方差矩阵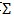 求特征向量,并将相应的特征值降序排序,选择前k个,就是我们需要的新维度(顺便说一句,特征向量彼此间是正交的)。
求特征向量,并将相应的特征值降序排序,选择前k个,就是我们需要的新维度(顺便说一句,特征向量彼此间是正交的)。
PCA的步骤为:
(1)对输入样本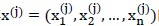 的每个维度,减去该所有样本在该维度的均值,并除以该维度样本数据的标准差;处理后的输入记作
的每个维度,减去该所有样本在该维度的均值,并除以该维度样本数据的标准差;处理后的输入记作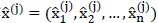 ;
;
(2)求解处理后样本间的协方差矩阵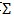 ;
;
(3)求解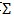 的特征值&特征向量;将特征值降序排序,选择前k个对应的特征向量(就是新的维度,是列向量)构成n*k矩阵;
的特征值&特征向量;将特征值降序排序,选择前k个对应的特征向量(就是新的维度,是列向量)构成n*k矩阵;
(4)将处理后的样本投影到k个特征向量:
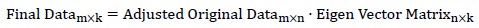
之后,我们就可以用这新的数据做各种学习。
6、线性判别分析(Linear Discriminant Analysis)
已有的数据是m个样本,每个样本有n个特征维度。即:
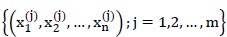
这其中有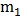 个样本属于
个样本属于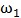 类别、有
类别、有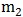 个样本属于
个样本属于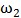 类别。注意这和Logistic回归的样本假设是一样的,仅仅是把输出由0/1变成了
类别。注意这和Logistic回归的样本假设是一样的,仅仅是把输出由0/1变成了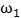 /
/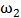 。
。
我们觉得n个特征维度太多,想将其降到只有一个维度;届时可以只用这一个维度来预测样本所属类别,因此,要求这一次降维能清晰的将不同类别的样本区分开来。
LDA采用的方法是:构建一个n维向量w,将样本投影到w,并根据投影点到原点的距离来判断样本类别。
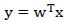
注意几点:(1)由平面几何知识,当w向量是经过原点的单位向量时,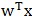 就是向量x在w上投影点到原点的距离;(2)y并非直接就是类别
就是向量x在w上投影点到原点的距离;(2)y并非直接就是类别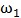 或
或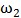 ,而是根据其值推断是属于
,而是根据其值推断是属于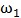 还是
还是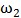 ,例如
,例如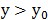 就判断为
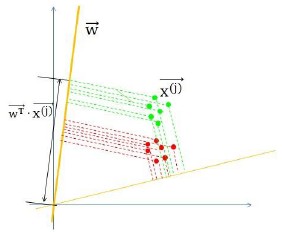
就判断为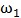 等;(3)从(2)来看,并不要求w是单位向量,只需把不同类别样本的投影点分散开就行,w成倍的增长不影响最终判断。
等;(3)从(2)来看,并不要求w是单位向量,只需把不同类别样本的投影点分散开就行,w成倍的增长不影响最终判断。
如上图所示,我们的目标就是寻找图中w那样的向量,它能将红色类别、绿色类别清晰的区分开;而另一个向量则未做到这一点。
定量角度来看,LDA认为这样的分类是最优的:两个类别的投影的中心点相距尽可能的远、各个类内部点的投影尽可能聚集在一起。
样本的中心点为:
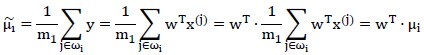
因此两类样本的中心点距离为:
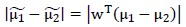
为衡量同一类内部点聚集程度,可采用“散列值”,如下:
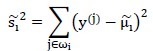
类似于方差,只是没有除以样本总数。
LDA用如下公式评价向量w的优劣:
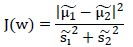
只要找出使J(w)最大的w就行。
以下叙述求解 的方法。
的方法。
散列矩阵可以写作:
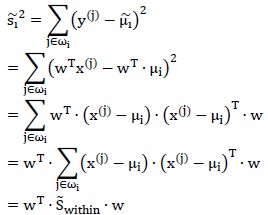
这里的w是n×1矩阵;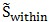 是n×n矩阵,并且很明显,若将其除以样本数量,就等价于协方差矩阵。
是n×n矩阵,并且很明显,若将其除以样本数量,就等价于协方差矩阵。
再将中心点距离的平方展开:
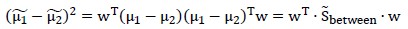
因此有:
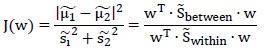
为了求解 这个最优问题,注意到向量w成倍的变化不影响结果,因此令分母等于1,构造Lagrange公式得:
这个最优问题,注意到向量w成倍的变化不影响结果,因此令分母等于1,构造Lagrange公式得:
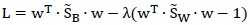
偏导为0得:

注意到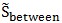 的表达式,
的表达式,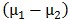 是常量(给定了样本点就是定值),因此有:
是常量(给定了样本点就是定值),因此有:
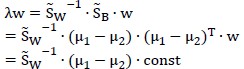
再考虑到w成倍变化对结果无影响,因此直接略去等号两边的常数项,有:
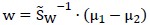
至此已经说明了如何寻找向量w,使得不同类别的样本被最大区分开。至于区分开后如何判别具体类别(例如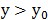 就判断为
就判断为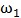 等,此时需要求解
等,此时需要求解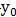 )暂未讨论。
)暂未讨论。
以下考察将LDA扩展到多类别情况。
此前仅有两个类别(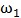 和
和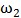 )、并且认为一维数据(n维样本输入x通过
)、并且认为一维数据(n维样本输入x通过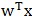 被降维)就足以判断类别。现在的场景是共有C个类别
被降维)就足以判断类别。现在的场景是共有C个类别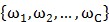 ;并且把样本输入由n维降到k维:矩阵
;并且把样本输入由n维降到k维:矩阵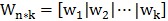 对输入x做变换,有
对输入x做变换,有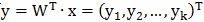 。
。
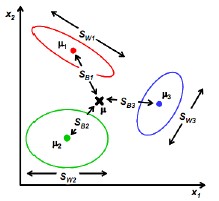
如图上所示,依旧是通过“不同类别样本投影的中心点间的距离”、“同类别样本点投影后的分散程度”两个维度衡量变换矩阵W。稍加改动的是,此前二值分类时,中心点间距离记作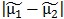 ;而多值分类时记作
;而多值分类时记作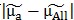 ,后者是所有样本中心点的投影。
,后者是所有样本中心点的投影。
样本总数记作m;样本类别有C个、记作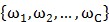 ;类别
;类别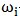 有
有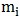 个样本。
个样本。
在当前基向量w(矩阵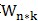 的某一列,n×1向量)上有:
的某一列,n×1向量)上有:
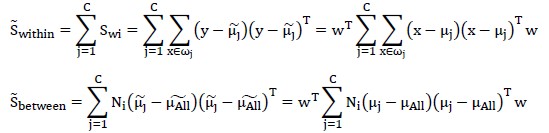
其中,对任一样本x,它在当前基向量w上的投影为:
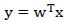
而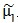 则是类别
则是类别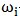 的全部
的全部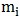 个样本在向量w上投影的中心点:
个样本在向量w上投影的中心点:
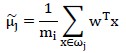
所有类别的所有样本在向量w上投影的中心点记作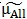 ,如下:
,如下:
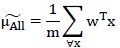
考虑所有k个基向量w,有:
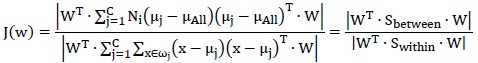
注意,原本分子分母都是k×k矩阵,因此对其求行列式;为求解J(w)的最大值,推导结果(不知道怎么推导的)是:
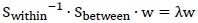
于是求解矩阵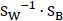 的特征值和特征向量,取特征值最大的k个对应的特征向量,作为基向量即可。
的特征值和特征向量,取特征值最大的k个对应的特征向量,作为基向量即可。
补充说明:(1)由矩阵的秩等知识,易知特征向量最多有C-1个;(2)由于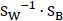 并非对称矩阵,所以特征向量间并不正交,这点与PCA不同。
并非对称矩阵,所以特征向量间并不正交,这点与PCA不同。
7、因子分析(Factor Analysis)
(1)
构建少数几个“假想变量”来反应原众多变量的主要信息。“假想变量”是不可观测的潜在变量,称为“因子”。
一个例子是,十项全能运动项目的成绩如下:

通过因子分析(并做旋转,后面会讲)可以得到如下表格:
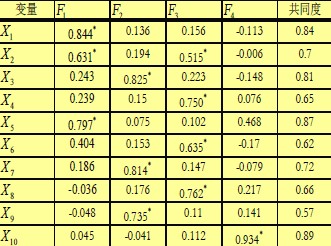
因子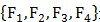 是通过数学方法计算出来的;计算之后,可以做直观解读:
是通过数学方法计算出来的;计算之后,可以做直观解读: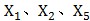 与
与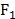 相关度很高,这三项运动需要短跑爆发力,因此
相关度很高,这三项运动需要短跑爆发力,因此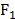 可称为“短跑速度因子”;
可称为“短跑速度因子”;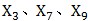 与
与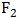 相关度很高,且这三者需要臂力,因此
相关度很高,且这三者需要臂力,因此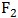 可称为“爆发性臂力因子”。
可称为“爆发性臂力因子”。
在此后的分析中,可以用这4个因子(即“假想变量”)来代替原先的10个变量。这是一种降维,与PCA、LDA的目的一样;只是降维方法不同。
(2)
因子分析方法的观点是,它认为n维的样本输入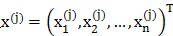 是由k(k<n)维空间里向量
是由k(k<n)维空间里向量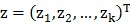 如下转换而来的:
如下转换而来的:
①在k维空间中按多元高斯分布,生成m个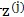 ,即
,即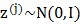 ;
;
②通过变换矩阵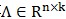 将
将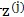 映射到n维空间,变成
映射到n维空间,变成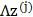 ;
;
③将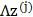 加上一个均值、n维向量
加上一个均值、n维向量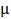 ,再加上误差
,再加上误差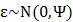 ;这时的结果被认为就是真实的样本输入,即
;这时的结果被认为就是真实的样本输入,即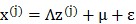 。
。

这也就是因子分析法降维的依据:它认为高维样本点是由低维样本,经过高斯分布、线性变换、误差扰动而生成的;因此高维数据可以由低维数据来表示。
(3)
在JerryLead的读书笔记中,介绍了“因子分析的EM估计”方法;具体来说,首先求出样本输入x的边缘分布,并得到最大似然估计的表达式,再使用EM算法求解最大似然估计。EM算法那一块没看明白,就说一下怎样计算最大似然函数。
我们认为x和z的联合分布是多元高斯分布,即:
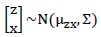
罗列一下此前的式子:
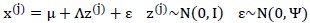
求解该多元高斯分布步骤如下:
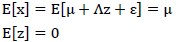
接下来求解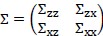 如下:
如下:
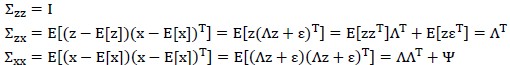
因此可得:
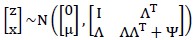
样本点的边缘分布为: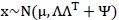 。
。
对全体样本点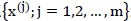 进行最大似然估计,如下:
进行最大似然估计,如下:
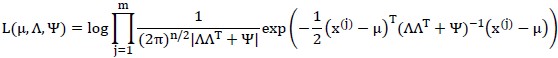
只需要求解偏导数为0,计算出转换矩阵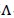 、误差协方差矩阵
、误差协方差矩阵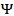 即可。但是因为隐变量的存在,使得最大似然函数不能直接求解,所以借助于EM算法。
即可。但是因为隐变量的存在,使得最大似然函数不能直接求解,所以借助于EM算法。




 本文深入探讨了机器学习中的关键概念,包括经验风险最小化、交叉验证、特征选择与提取,以及主成分分析、线性判别分析和因子分析等降维技术。详细解释了这些方法的原理和应用,为理解和实施机器学习算法提供了坚实的理论基础。
本文深入探讨了机器学习中的关键概念,包括经验风险最小化、交叉验证、特征选择与提取,以及主成分分析、线性判别分析和因子分析等降维技术。详细解释了这些方法的原理和应用,为理解和实施机器学习算法提供了坚实的理论基础。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








