文献阅读：EGO-Planner_ An ESDF-free Gradient-based Local Planner for Quadrotors

最新推荐文章于 2025-11-16 12:48:51 发布

原创最新推荐文章于 2025-11-16 12:48:51 发布 · 1k 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #动态规划 #无人机

前言

代码：ZJU-FAST-Lab/ego-planner (github.com)

论文：EGO-Planner: An ESDF-Free Gradient-Based Local Planner for Quadrotors | IEEE Journals & Magazine | IEEE Xplore

灰字为相关名词及细节的解释。

1.概述

基于梯度的局部规划器往往依赖于预先构建的ESDF（欧几里得有符号距离场）地图来评估梯度的大小和方向，并使用数值优化来生成局部最优解。

梯度：在机器人路径规划中，梯度通常指的是距离场（如ESDF）在空间中的变化率。它是一个向量，指向距离增加最快的方向。

ESDF中的梯度：ESDF（欧几里得有符号距离场）为空间中的每个点提供到最近障碍物的距离。ESDF的梯度在每个点给出了距离变化最快的方向。传统方法需要预先计算整个空间的ESDF来获取梯度信息。

局部最优往往在整体上并不是最优的；轨迹优化过程仅覆盖了ESDF更新范围的一个非常有限的子空间，因此计算这样一个场具有很大的冗余性。

创新点提出了一种无需ESDF的基于梯度的四旋翼局部规划方法。这种方法显著减少了计算时间，同时保持了与现有方法相当的性能。

2.避障估计

1.生成一条满足终端约束的简单B样条曲线 $\phi$ ，不考虑碰撞

2.进行迭代，每检测到碰撞段，生成一条无碰撞路径 $\Gamma$ 。如图（a）

利用一种图搜索算法A*生成无碰撞路径。A*使用成本函数f(n) = g(n) + h(n)；g(n)是从起点到当前节点的实际成本。h(n)是从当前节点到目标的估计成本（启发函数）。选择f(n)最小的节点进行扩展。虽然A*生成的路径可能不是很平滑，但它为后续的B样条优化提供了一个很好的初始参考。

3.如图b对于碰撞路径上的每一个控制点 $^{Q_{i}}$ ，首先计算其切线向量 $^{R_{i}}= \left ( ^{Q_{i+1}}-^{Q_{i-1}} \right )/2\Delta t$ ，构造一个垂直于此向量且过控制点 $^{Q_{i}}$ 的平面 $\Psi$ 与无碰撞路径 $\Gamma$ 交于直线 $l$ ；确定一点p为直线 $l$ 上最接近控制点 $^{Q_{i}}$ 的点，且在障碍物表面；接着计算由控制点指向p的单位向量，形成 $\left ( p,v \right )$ 对。

4.如图c定义距离场 $^{d_{ij}}= \left ( ^{Q_{i}}- ^{p_{ij}} \right )\cdot ^{v_{ij}}$ ，当 $^{d_{ij}}$ 小于0时代表控制点在障碍物内部，即图c中蓝色部分。

这里的Q和P都是点在空间内的三维坐标；这里的Qi指的是为了避障寻找的新控制点。这里计算距离场主要是用于后面构建碰撞惩罚项以及帮助生成碰撞力。

避免计算冗余：只有当Qi处于障碍物中，且当前得到的所有dij都大于0，则将障碍物定义为新障碍物，这样可以只计算影响轨迹的障碍物信息，减少运行时间。

如下算法实现了以上过程：

输入包括环境信息 $\varepsilon$ ，控制点Q

1.检测连续碰撞段（3-7）

遍历控制点、找出连续碰撞段，碰撞段信息存储在S中

2.生成避障路径（8-9）

对于每个碰撞段Si，使用A*生成一条无碰撞路径

3.生成避障信息（10-13）

对于每个控制点Qi，找到所有 $\left ( p,v \right )$ 对，存储。

3.基于梯度的轨迹优化

轨迹表示：文中构造的B样条曲线是均匀B样条曲线，每个控制点间的 $\Delta t$ 是一样的，故每个点的速度，加速度，加加速度可求得：

优化目标：最小化成本函数 $J$ ，由平滑项 $J_{s}$ 、碰撞项 $J_{c}$ 、动力学 $J_{d}$ 三项构成， $\lambda$ 为各项权重。

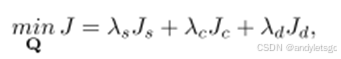
平滑度惩罚：

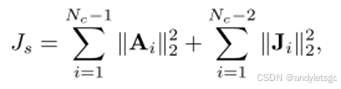
目的：最小化轨迹的加速度和加加速度，由于B样条曲线的凸包特性，如果控制点序列是平滑的（最小化轨迹的加速度和加加速度），那么由这些控制点生成的B样条曲线也会是平滑的。

平方L2范数，值为向量空间中每个值的平方和 Nc为控制点数量

凸包：B样条曲线完全包含在其控制点所形成的凸包内

碰撞惩罚：

构建了一个二次连续可微惩罚函数，引入了安全间隙 $s_{f}$ ， $c_j$ 为安全间隙减去到最近障碍物的距离，小于等于0即为安全

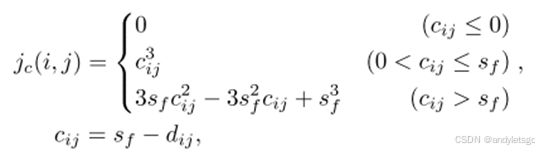
总碰撞惩罚：

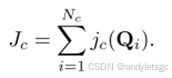
直接用惩罚函数对控制点求导获得梯度

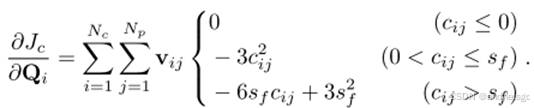
（动力学）可行性惩罚：

目的：确保轨迹满足动力学约束

方法：限制轨迹在每个维度上的高阶导数

$J_d$ 是总的可行性惩罚

$w$ 分别是速度、加速度和加加速度的权重

$V_i A_i J_i$ 分别表示控制点的速度、加速度和加加速度

$F\left ( \cdot \right )$ 是一个度量函数，用于评估每个导数项的违反程度

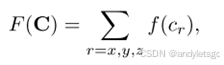
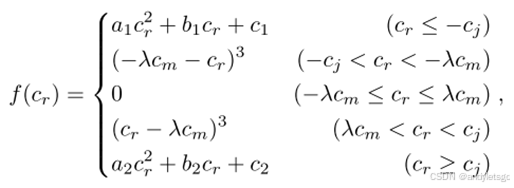
其中 $c_r$ 是C中的一个分量（可以是速度、加速度或加加速度的x、y、z分量）； $c_m$ 表示对应导数的限制值，其具体数值需要根据四旋翼飞行器的动力学特性来确定,以保证生成的轨迹在飞行器的动力学能力范围内； $c_j$ 表示二次区间和三次区间的分割点，可能是一个需要根据具体问题调节的超参数； $\lambda$ 为弹性系数，取值小于 $1-\varepsilon$ ( $\varepsilon$ 是一个很小的正数)，用于使最终结果满足约束条件；a1, b1, c1, a2, b2, c2为用于满足二阶连续性的系数。

这个分段函数的设计目的是:

当导数值在限制范围内时 $\left [ -\lambda c_m ,\lambda c_m\right ]$ ，不施加惩罚

当导数值接近但超出限制时,使用三次函数平滑过渡

当导数值远超限制时,使用二次函数快速增大惩罚

通过这种设计,可以在保证轨迹动力学可行性的同时,避免优化过程中的突变。

4.数值优化

上述的优化函数J会根据新发现的障碍物自适应变化，这要求求解器能快速重启，其近似二次函数，利用Hessian信息可以显著加速收敛。由于精确计算Hessian逆矩阵在实时应用中计算量太大，文章采用了拟牛顿法来近似Hessian逆矩阵，文章比较了三种拟牛顿算法：Barzilai-Borwein方法、截断牛顿法和L-BFGS方法。最终选择了L-BFGS算法，因为它在重启损失和Hessian逆矩阵估计精度之间取得了良好平衡。

优化目标函数：

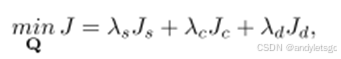
对于无约束优化问题 min f(x), x∈R^n, L-BFGS的更新步骤为：

x(k+1)=x(k) - α(k) * H(k) * ∇f(k)

其中α(k)是步长,H(k)是Hessian矩阵的近似逆。

H(k)的更新公式为:

H(k+1)= V(k)^T * H(k) * V(k) + ρ(k) * s(k) * s(k)^T

其中，ρ(k)= 1 / (y(k)^T * s(k))，V(k)=I - ρ(k) * y(k) * s(k)^T，s(k)=x(k+1) - x(k)，y(k)=∇f(k+1) - ∇f(k)

不直接计算H(k),而是通过两步循环递归法来计算H(k) * ∇f(k)。只存储最近m次迭代的{s(k), y(k)}对，用于近似H(k)。初始H(0)可以设为:

H(0) = (s(k-1)^T * y(k-1)) / (y(k-1)^T * y(k-1)) * I

或

H(0) = (s(k-1)^T * s(k-1)) / (s(k-1)^T * y(k-1)) * I

使用强Wolfe条件的单调线搜索来确保收敛。

强Wolfe条件的单调线搜索是一种用于确定优化算法中步长的方法。这种方法在确保算法收敛的同时，也能提高算法的效率。

通过上面的步骤得到了安全轨迹Φs (safe trajectory)，过程为：

1.初始化一条简单轨迹。

2.检测碰撞,为碰撞点添加障碍物信息。

3.评估惩罚函数和梯度。

4.进行一步优化。

5.重复以上步骤直到无碰撞。

5. 时间重新分配和进一步轨迹优化

在轨迹优化之前无法准确分配时间,因为此时规划器对最终轨迹没有足够信息。需要额外的时间重新分配程序来确保动力学可行性,即满足速度、加速度等约束。

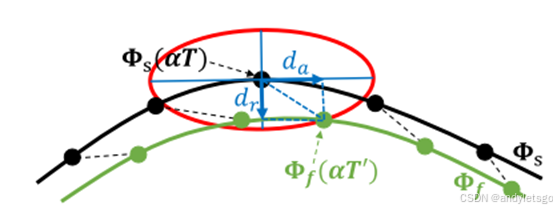
方法：基于前面部分得到的安全轨迹Φs，重新生成一个时间分配合理的均匀B样条轨迹Φf。提出各向异性曲线拟合方法，使Φf能自由优化控制点以满足高阶导数约束，同时保持与Φs几乎相同的形状。

时间重新分配具体步骤：

1.计算超出限制的比率

其中Vi,r, Aj,r, Jk,r分别是速度、加速度、加加速度在r轴上的分量,vm, am, jm是对应的限制值。

超出限制的比率re表示新生成的轨迹Φf相对于原始安全轨迹Φs应该延长多少时间分配，re的值表明了需要将原始时间分配延长多少倍,以满足动力学约束。

2.根据re计算新的时间跨度:

3.生成时间跨度为Δt'的Φf,保持与Φs相同的形状和控制点数量。

通过求解一个闭式最小二乘问题来初始生成Φf，大致步骤如下：

已知新的时间跨度Δt'；

设置约束条件:保持与Φs相同的控制点数量，满足边界约束(起始和终止状态)，保持与Φs相似的整体形状；

构建最小二乘问题:目标函数:最小化Φf与Φs之间的误差，变量:Φf的控制点位置，约束:边界条件和控制点数量；

求解闭式最小二乘问题:使用标准的最小二乘求解方法(如正规方程法)，得到一组满足约束的Φf控制点位置；

生成初始Φf:使用求解得到的控制点位置，应用新的时间跨度Δt'，生成一条均匀B样条曲线作为初始Φf；

后续处理:这个初始生成的Φf会作为后续优化的起点，进一步优化以满足动力学约束和提高轨迹质量。

轨迹优化：

目标函数：

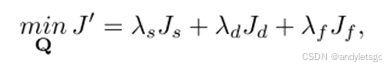
其中Js是平滑性项，Jd是可行性项，Jf是曲线拟合项，λs、λd、λf是权重。

引入各向异性位移积分Jf作为拟合惩罚函数

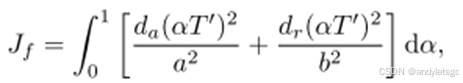
其中da和dr分别是轴向和径向位移，a和b是椭圆的半长轴和半短轴。

由于是椭圆，如上面的图，轴向位移(da)给予低惩罚权重，允许轨迹在切线方向有更大的调整空间。径向位移(dr)给予高惩罚权重，严格限制轨迹偏离原始安全轨迹，避免碰撞。通过旋转椭圆形成椭球体，实现各向异性惩罚，更灵活地平衡安全性和平滑性。

同样用L-BFGS算法求解优化问题。

如下算法实现以上过程：

符号定义:

G: 目标点E: 环境Q: 控制点结构J: 惩罚函数G: 梯度

初始化:（第二行）

根据上一次的控制点和目标点初始化控制点Q。

主循环:（3-7）

当轨迹不是无碰撞的，执行以下步骤:

a.检查并添加障碍物信息,这一步调用了算法1。

b.评估惩罚函数J和梯度G。

c.进行一步优化更新控制点Q。

可行性检查和优化:（8-11）

如果轨迹不满足动力学可行性,执行以下步骤:

a.重新分配时间。

b.进行曲线拟合优化。

6.实验结果

1.实现细节：

使用3阶B样条曲线

控制点数量约为25个

规划范围约7米

相邻控制点初始间距约0.3米

使用A*算法进行无碰撞路径搜索

对最终轨迹进行固定半径的圆管碰撞检查以确保安全性

优化算法比较：

比较了三种优化算法：Barzilai-Borwein (BB)方法、L-BFGS方法和截断牛顿(Truncated Newton)方法。结果显示L-BFGS性能最佳，成功率和计算时间都优于其他两种方法。

2.有无ESDF的轨迹生成比较：

比较了EGO（无ESDF）、ENI（有ESDF，无碰撞初始化）和EI（有ESDF，有碰撞初始化）三种方法。结果显示EGO在成功率和计算时间上表现优秀，但轨迹能量略高。

3.多个规划器的比较：

将EGO-Planner与Fast-Planner和EWOK进行了比较。EGO-Planner在飞行时间和轨迹长度上表现最佳，但能量消耗略高。计算时间方面，由于不需要更新ESDF，EGO-Planner显著优于其他两种方法。

室内实验：在狭窄空间（不到1米宽）中飞行，最高速度达到3.56m/s

室外实验：在树木和灌木丛中飞行，速度超过3m/s

动态目标追踪实验：验证了规划器在有限视野下快速生成可行轨迹的能力

总的来说，实验结果表明EGO-Planner在不使用ESDF的情况下，能够达到与现有最先进方法相当的性能，同时显著减少了计算时间。